Оглавление:
Частные случаи вращательного движения твердого тела
Равномерное вращение
Равномерным вращением тела называется вращение тела с постоянной угловой скоростью. В этом случае
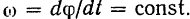
Пусть при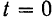 
угол поворота тела 
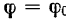. Разделяя переменные в предыдущем равенстве и интегрируя его в соответствующих пределах, будем иметь
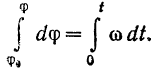
Отсюда
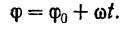
Уравнение (88) называется уравнением равномерного вращения тела.
Уравнение (88) выведено из условия, что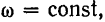 
и поэтому оно применимо лишь для случая равномерного вращения тела.
Угловое ускорение тела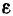 
при равномерном его вращении, очевидно, равно нулю. Отсюда следует, что при равномерном вращении тела вращательное ускорение любой его точки 
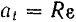также всегда равно нулю. Таким образом, полное ускорение точки равномерно вращающегося тела состоит только из одного центростремительного ускорения
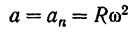
и направлено, конечно, к центру окружности, описываемой данной точкой.
Равномерно переменное вращение
Равномерно переменным (равномерно ускоренным или равномерно замедленным) вращением тела называется такое его вращательное движение, при котором за равные, произвольно взятые промежутки времени угловая скорость тела меняется на одну и ту же величину.
Очевидно, что при равномерно переменном вращении тела его угловое ускорение постоянно:
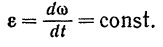
Пусть при 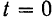угловая скорость тела 
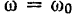. Разделяя переменные в предыдущем равенстве и интегрируя его в соответствующих пределах, будем иметь:
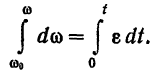
Отсюда получается формула угловой скорости тела при его равномерно переменном вращении
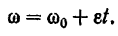
Заменяя в последнем равенстве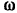 
его значением 
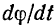, будем иметь:
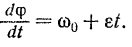
Пусть при 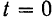угол поворота тела 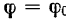. Тогда, разделяя переменные в предыдущем равенстве и интегрируя его в соответствующих пределах, находим
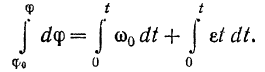
Отсюда получается уравнение равномерно переменного вращения тела
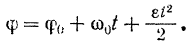
Формулы (89) и (90) выведены из условия
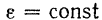
и, следовательно, они применимы лишь для случая равномерно переменного вращения тела. В этих формулах под 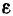понимается алгебраическое значение углового ускорения тела, положительное при ускоренном вращении и отрицательное при замедленном.
Очевидно, что при равномерно переменном вращении тела все его точки совершают равномерно переменное движение по окружностям соответствующих радиусов, а потому для определения их движения применимы формулы, установленные в § 49.
С равномерно переменным вращением мы обычно встречаемся в задачах, связанных с пуском и остановкой машины. Угловое ускорение тела, как это будет доказано в динамике, есть величина постоянная в случае постоянной величины приложенного к телу вращающего момента сил.
Полезно для запоминания обратить внимание на аналогии, существующие между формулами кинематики точки и формулами для соответствующих случаев вращательного движения твердого тела. Нетрудно заметить, что для перехода от первых формул ко вторым требуется лишь заменить в них дуговую координату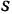 
точки углом поворота 
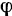тела, скорость 
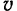точки — угловой скоростью 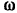тела и касательное ускорение 
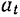точки — угловым ускорением 
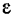тела.
Пример задачи:
Шкив радиусом 0,3 м, вращаясь равномерно, делает 1200 об /мин. Найти его угловую скорость а также скорость 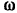, и ускорение точки, лежащей на окружности шкива.
Решение:
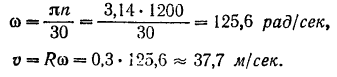
Так как при равномерном вращении тела вращательное ускорение
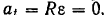
то полное ускорение
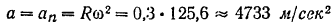
и направлено к центру шкива.
Пример задачи 44.
Тело, вращаясь равномерно ускоренно из состояния покоя, приобрело в течение 10 сек угловую скорость, равную 30 рад/сек. Сколько оборотов сделало тело за эти 10 сек?
Решение:
По условию задачи начальная угловая скорость тела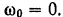 
. Так как вращение тела — равномерно переменное, то его угловое ускорение
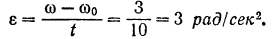
Приращение угла поворота тела за 10 сек равно
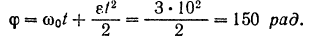
Зная угол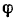 
поворота, определяем соответствующее ему число оборотов тела:
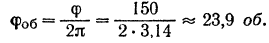
Пример задачи:
Маховик, имевший угловую скорость в 600 об/мин, был предоставлен самому себе и вследствие трения в подшипниках остановился, сделав 200 оборотов. Определить угловое ускорение колоса, считая его постоянным.
Решение:
Определяем угол поворота маховика, соответствующий сделанным до остановки 200 оборотам:
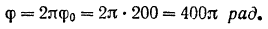
Начальная угловая скорость маховика
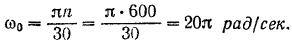
Конечная угловая скорость маховика
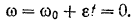
При равномерно переменном вращении тела угол его поворота определяется формулой
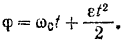
Решая эти два уравнения совместно, находим
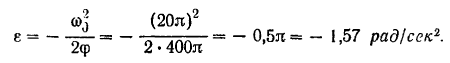
Отрицательное значение 8 говорит о замедленном вращении маховика.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
