Оглавление:
Частные случаи движения точки
Равномерное движение
Равномерным движением называется, как мы знаем, таксе движение, при котором точка за любые равные промежутки времени проходит равные расстояния.
Очевидно, что величина скорости в этом движении
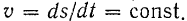
Отсюда
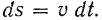
Пусть в начальный момент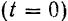 
точка находилась от начала отсчета на расстоянии 
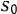. Тогда интегрируя предыдущее уравнение в соответствующих пределах, будем иметь:
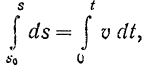
откуда расстояние точки от начала отсчета расстояний
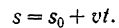
Уравнение (71) определяет равномерное движение точки. Из формулы
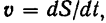
где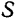 
— путь, пройденный точкой, аналогичным образом находим:
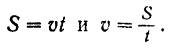
Скорость точки при равномерном движении (и только при этом движении) равна отношению пройденного пути ко времени. Так как модуль скорости точки остается постоянным при любом равномерном ее движении, то при этом всегда ее касательное ускорение
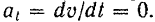
Отсюда следует, что касательное ускорение точки характеризует изменение ее скорости по величине.
При равномерном криволинейном движении точки ее скорость, оставаясь постоянной по модулю, изменяется только по направлению. Полное ускорение точки в этом случае равно нормальному ускорению, а
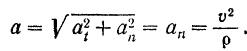
Отсюда следует, что нормальное ускорение точки характеризует изменение ее скорости по направлению.
Прямолинейное движение
При прямолинейном движении точки радиус кривизны ее траектории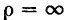 
и нормальное ускорение точки
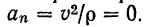
Следовательно, полное ускорение точки
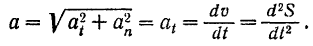
При прямолинейном движении точка может иметь только одно касательное ускорение, и потому ее полное ускорение равно первой производной по времени от алгебраического значения скорости или второй производной по времени от пройденного ею пути.
Заметим, что так определяется ускорение точки только при прямолинейном ее движении.
В случае, если точка совершает прямолинейное и равномерное движение, то и нормальное
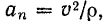
и касательное
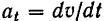
(следовательно, и полное) ускорения точки будут тождественно равны нулю. В этом движении точка не имеет никакого ускорения, так как ее скорость остается все время постоянной как по модулю, так и по направлению.
Равномерно переменное движение
Часто встречающимся на практике равномерно переменным (равномерно ускоренным или равномерно замедленным) движением точки называется такое ее движение, когда в равные, произвольно взятые промежутки времени алгебраическое значение скорости точки изменяется на одну и ту же величину.
Изменение алгебраического значения скорости точки характеризуется, как мы знаем, касательным ускорением. Отсюда следует, что при равномерно переменном движении точки алгебраическая величина ее касательного ускорения
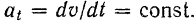
Разделяя переменные и интегрируя уравнение в соответствующих пределах, будем иметь:
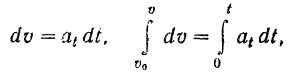
где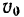 
— величина скорости в начальный момент времени. Отсюда
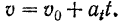
Для вывода уравнения движения точки воспользуемся зависимостью (67), из которой находим
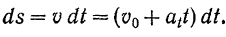
Полагая при
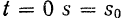
и интегрируя это уравнение в соответствующих пределах, получаем:
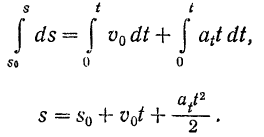
Уравнение (74) представляет собой уравнение равномерно переменного движения точки. Из формулы
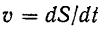
аналогичным образом находим
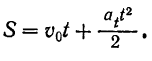
В этих формулах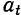 
берется положительным при ускоренном движении и отрицательным — при замедленном.
Формулы (73), (74) и (74а) одинаково справедливы как для прямолинейного, так и для криволинейного равномерно переменного движения точки. При прямолинейном движении точки радиус кривизны траектории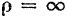 
и нормальное ускорение точки
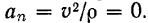
Следовательно, в этом случае ее полное ускорение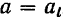 
Поэтому обычно, применяя данные формулы к прямолинейному равномерно переменному движению точки, индекс 
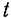в обозначении ускорения опускают.
Гармоническое колебательное движение
Гармоническим колебанием точки называется такое ее движение, при котором расстояние s точки от начала отсчета изменяется по закону:
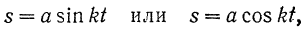
где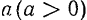 
и 
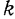— постоянные величины.
Так как значения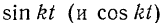 
изменяются в пределах от —1 до +1, то расстояния s точки от начала 
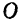обсчета изменяются в пределах 
.
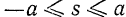Наибольшее расстояние а, на которое точка удаляется от начала отсчета, называется амплитудой колебания.
Время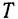 
одного полного колебания точки называется периодом колебания. Очевидно, что в начале и в конце промежутка времени 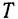точка должна находиться на одном и том же расстоянии от центра. Для этого необходимо, чтобы аргумент у синуса (или косинуса), входящего в правую часть равенства (75), изменялся на величину 
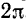, т. е. чтобы имело место следующее равенство:
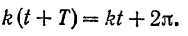
Отсюда находим, что период колебания точки
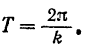
Постоянная 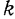, показывающая, сколько полных колебаний точка совершает за 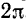секунд, называется круговой частотой колебаний. Ее размерность — 
.
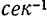Пример задачи:
Поезд, двигаясь по закруглению пути равномерно ускоренно, приобретает через 3 мин после отхода от станции скорость
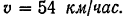
Определить ускорение поезда через 2 мин после отхода от станции, если радиус закругления пути
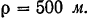
Решение:
Полагая
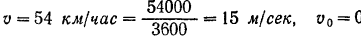
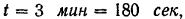
из формулы (73) определяем касательное ускорение поезда:
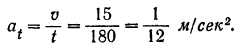
Так как движение поезда — равномерно ускоренное, то его касательное ускорение постоянно.
Нормальное же ускорение поезда, определяемое формулой (69),
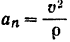
зависит от скорости движения и будет различным для разных моментов времени.
Определяем скорость поезда в конце второй минуты после отхода его от станции
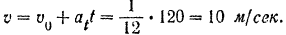
Тогда нормальное ускорение поезда в этот момент будет равно
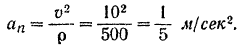
Ускорение (полное) поезда в конце второй минуты
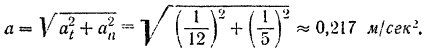
Пример задачи:
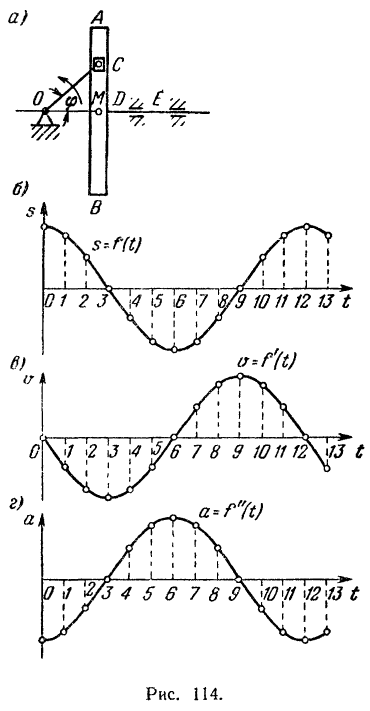
Жестко связанная с направляющей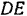 
(рис. 114, а) рама 
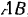, называемая обычно кулисой, приводится в движение кривошипом 
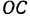(расположенным впереди рамы и направляющей). Кривошип вращается вокруг точки 
равномерно, причем угол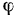 
изменяется со временем по закону 
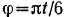. Концом 
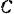кривошип шарнирно соединен с ползуном, скользящим в прорези рамы. Длина кривошипа 
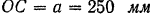. Определить движение рамы и построить графики движения, скорости и ускорения.
Решение:
При вращении кривошипа рама 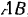совершает колебательное движение около точки , причем все точки рамы совершают одинаковое прямолинейное движение. Рассмотрим движение какой-нибудь одной точки рамы, например, ее середины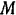 
. Траекторией этой точки будет прямая, совпадающая с осью движения ползуна. Примем неподвижную точку (центр вращения кривошипа) за начало отсчета расстояний и напишем уравнение движения точки 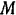. За положительное направление отсчета расстояний примем направление вправо от точки . Из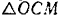 
(рис. 114,а) имеем:
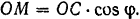
Обозначив расстояние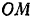 
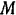точки от начала отсчета через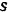 
и приняв во внимание, что 
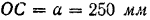и угол 
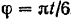, будем иметь:
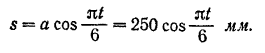
Полученное уравнение (I) аналогично уравнению (75).
Точка 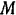и рама 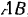совершают гармоническое колебательное движение около неподвижного центра . Из сравнения уравнений (I) и (75) ясно, что амплитуда этого колебания
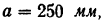
круговая частота
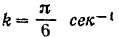
и период колебаний
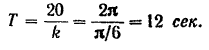
За 12 секунд кривошип 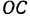делает один оборот, а рама 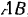совершает одно полное колебание. Графиком движения 
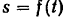точки 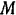будет косинусоида, изображенная на рис. 114,6.
Дифференцируя по времени уравнение движения точки 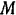, находим величину скорости
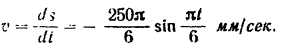
Графиком скорости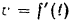 
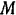точки будет синусоида, изображенная на рис. 114, в.
Так как точка 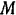совершает прямолинейное движение, то ее ускорение
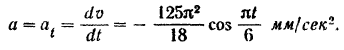
Графиком ускорения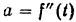 
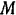точки будет косинусоида, изображенная па рис. 111, с’.
Из уравнения (1) движения точки 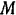и из выражений для ее скорости (II) и ускорения (III) видно, что скорость и ускорение точки изменяются периодически. В начальный момент, при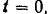 
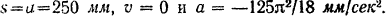
Следовательно, в этот момент точка 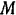находится в крайнем («мертвом») положении, скорость ее равна нулю, ускорение максимально по абсолютной величине и отрицательно, т. е. направлено в сторону, противоположную направлению отсчета расстояний (справа налево).
При дальнейшем движении точки 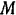к центру ее скорость увеличивается по абсолютному значению, а ускорение уменьшается, оставаясь направленным в сторону движения точки, В момент, когда точка 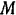будет находиться в центре 
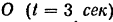, ее скорость достигнет максимальной величины, ускорение же будет равно нулю. При дальнейшем движении точки (от точки до крайнего левого положения) ее скорость по модулю будет уменьшаться, ускорение же увеличивается и направлено в сторону, противоположную движению точки (слева направо).
Таким образом, когда точка находится в центре колебания, ее скорость максимальна по модулю, а ускорение равно нулю. В крайних же положениях скорость точки равна нулю, а ускорение по модулю максимально. От центра колебаний к крайнему положению точка движется замедленно. От крайнего же положения к центру колебаний точка движется ускоренно.
В рассмотренном примере мы имели дело с прямолинейным движением точки, но гармонические колебания точка может совершать и по любой криволинейной траектории. Характер движения точки будет тот же, только при этом надо иметь в виду, что при криволинейном движении, кроме касательного ускорения, точка имеет еще и нормальное ускорение.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
