Оглавление:
Частные производные высших порядков
Частные производные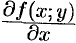 
и 
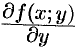называют частными производными первого порядка. Их можно рассматривать как функции от 
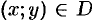. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
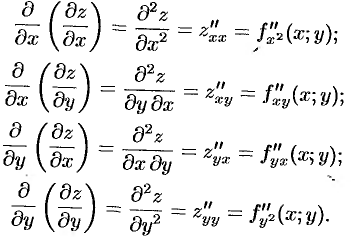
Аналогично определяются частные производные 3-го, 4-го и т. д. порядков. Так,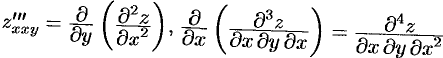 
(или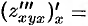 
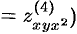и т. д.
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например,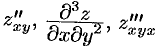 
.
Пример №44.2.
Найти частные производные второго порядка функции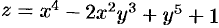 
.
Решение:
Так как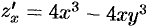 
и 
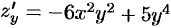, то
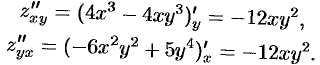
Оказалось,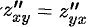 
.
Этот результат не случаен. Имеет место теорема, которую приведем без доказательства.
Теорема 44.1 (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой. В частности, для 
имеем: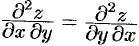 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
