Оглавление:



Частные случаи
- Особый случай Сечение асимметричное. Сжимающее усилие P прикладывается к центральной линии (ey = ay \ ex = ar). Критическая сила определяется как три минимальных значения P p . p _ p _ ^ E J y
‘1- * Y p ♦ * 2 * 2 ^ 2 P G2 r> ® (9,20) где 2. где + -f-az + -r-dy-a 2-a2 4 2 J y 4 (9,21) ^ E J a G j K r r 2 «Гr 2 • секция имеет две оси симметрии. Сила приложена к оси симметрии (эй-0). 2 1 _ Jy + Jz p _ p. —
f, G1-r Zt р а р у + па £ p- (P y-P ^ + ^ P y P v 2 2 р- $ Сечение асимметричное. Сила Людмила Фирмаль
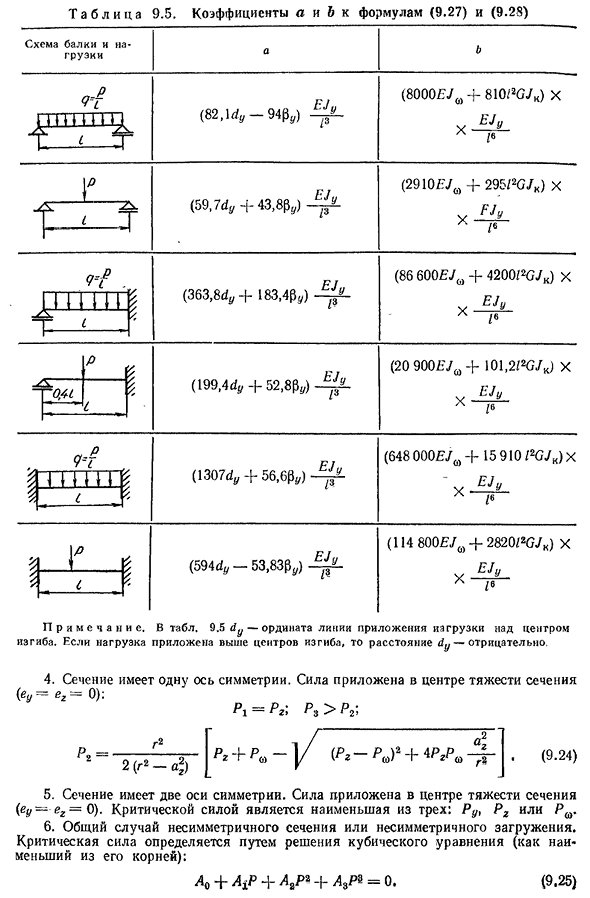
применяется к центру тяжести поперечного сечения {eu-eg = критическая сила определяется из уравнения: (9,22) (9,23) 218T Таблица 9.5. Коэффициенты a и b в уравнениях (9.27) и (9.28) Диаграмма луча и нагрузки a b <7-г (82, ИД-94 с.) (8000nJa + 810 / 2G JK) X E Jy X / G —- ZS. T (59,7 д. + 43,8 трения) (2910EJffl + 295 / 2G JK) X x F J » X
/ In t p 1 n (3 6 3, 8 д. + 183,4 стр.) (86 600EJM + 4200 / 2G JK) X «E J ты X / 6 и р Я (199.4дюйм + 52.8 трение) (20 900E / w + 101,2 / 2G / K) XE Y. X V0.41 —- 1 N и 1 D: Я ✓ / (1307d. + 56,6P.) (648 000E / ffl + 1 5910 / 2G JK) X-x E J y Z е (5 9 4 д. — 53,83 р.) (114 800E / ffl + 2820 / 2G JK) X E J y X I * Примечание 1 в таблице. 9,5 d y-ордината приложенной линии нагрузки над
- центром изгиба. Если нагрузка приложена выше центра изгиба, расстояние dy будет отрицательным. 4. Сечение имеет одну ось симметрии. Сила применяется к центру тяжести секции (eu = eg = 0): P l-P g ′, P s ^ P g ’′ 2 (9,24) 5. В поперечном сечении есть две оси симметрии. Сила приложена к центру тяжести поперечного сечения (ey = e g = 0). Критическая сила — это три минимальных значения Ru, Pg или Pa. 6. Общий случай асимметричного сечения или несимметричной нагрузки. Критическая сила определяется путем
решения кубического уравнения (в качестве его корневого минимума). 4 секунды ^ = 0. (9,25) 216 минимальный маршрут P cr = …… ————-, (9,26) V L, 4 «ZLdL3-ZL0L1L2 где 0 0 = -r ^ ryPrP (0> 11 = r * PvPa + rРPrPr + PyPr (r2 + 2 ^ r + 2 | ^); La = -rm Pm-Py (r2-2-2ftze2 4-2 (] уеу-d2) -Рг (r * 4 ~ 2Pz? z + 2flyev ^)> Л3 = r? 4-2ruе + 2 ^ rd} -d2-, dy = Clу & y \ dz = Пгe2 ‘Для тонкой стены с боковой нагрузкой
При расчете устойчивости формы плоского изгиба стержень использует следующее соотношение: Если поперечное сечение имеет одну ось Людмила Фирмаль
симметрии: ^ кр- ^ кр- ^ О; (9-27) Если есть две оси симметрии и две нагрузки, это применяется к центру тяжести, и критическая сила Пкр = V б. В таблице приведены коэффициенты a и b, включенные в уравнения (9.28) (9.27) и (9.28) для различных фиксированных и нагрузочных случаев. 9.5. Положительный корень уравнения (9.27) n (9.28) соответствует приложению нагрузки вертикально вниз, а отрицательного — вверх. Вышеуказанная зависимость полезна, когда напряжение пучка не превышает предел пропорциональности.
Смотрите также:
| Расчет по бимоментам | Поступательное движение стержня |
| Устойчивость тонкостенных стержней | Вращающиеся стержневые системы |

