Оглавление:


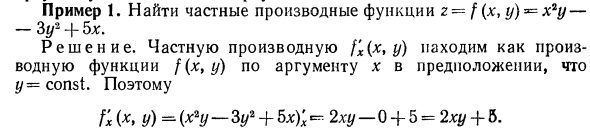



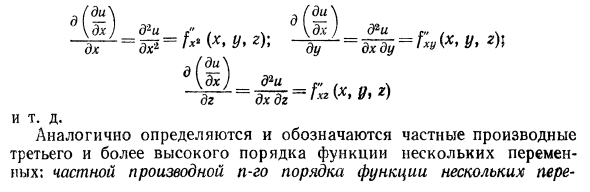


Частные производные
- Частные деривативы /. Первая частная производная Рассмотрим функцию с двумя переменными r = f (x, y). Измените один из аргументов, например, y, и установите y = y0. В этом случае функция / (xy y o) является функцией одной переменной x. Дайте x0 производную. lim /(o+A.yo)-f(*o, йо) Эта производная называется частной производной (или частной производной первого порядка) функции z- / (x, y) по x в точке P0 (a’0; y0) f’x (x®> ) •
D ** = / (* 0 + L * .Yo) — / (7) Учитывая эти обозначения, Tx (x0, y0) = lim (8) DL-0 Частичное приращение функции z = f (x, y) относительно y и частная производная по y в этой точке определены и показаны.
Разность f (x0 + Ax, * / „) -f (x0, y0) называется частичным приращением x функции zf (x, y) в точке P0 (x0 \ y0) и обозначается символом Axz вы. Людмила Фирмаль
(Lo »W o) ‘ V = f (* o> Yo + Ao) — / oo). Gu (Xb, Yo) = Hn-> r • Du-o LU Таким образом, частная производная функции двух переменных по одному из аргументов равна пределу отношения между частичным приращением функции и приращением аргумента, вызвавшего ее, когда приращение аргумента стремится к нулю.
Это становится. Значение частной производной зависит от точки P (x *; y), где она рассчитана. Следовательно, частная производная функции двух переменных z-f (x, y), как правило, является функцией точки P (x \ y). Это также функция двух переменных x и y. Частная производная, которая считается функцией двух переменных, показана как fxfay), fy (x> y) или h или 37. * • Частичные приращения и частные производные функций от n переменных с n> 2 определены и показаны также.
| Функции нескольких переменных | Полный дифференциал функции |
| Предел функции нескольких переменных» непрерывность функции. Точки разрыва | Дифференцирование сложных и неявных функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Например, для функции трех переменных u- / (x, y, z), если * получает приращение Ax, а остальные аргументы не изменяются, частичное приращение x в точке P0 (x0 \ y0 \ zn) Приобретается. \ xu = f (xb + bx, y99 z0) -f (x0, yot z0). (10) Частная производная функции u = f (x, y, z) по аргументу x точки Po (* §; Yo’u 20) имеет вид U o * go) = linl TTJ. (1!) д * -0 Ач Следовательно, частная производная функции некоторых переменных определяется как производная любой функции этих переменных.
Обратите внимание, что во всех этих правилах и выражениях все остальные аргументы считаются константами при поиске частных производных по аргументам.
В результате все правила и производные формулы, полученные для производной функции одной переменной, сохраняются для частной производной функции нескольких переменных. Людмила Фирмаль
Пример 1. Найти частную производную функции z = f (x, y) * = x * y — 3/2 + 5 *. Решения. Найти частную производную f’x (x, y) как производную функции f (x, y) по аргументу x в предположении, что y = const. так fx (x, y) = (xy-3y2 + 5 *); -2hu -0-f5 = 2hu + b. Как хорошо fy (x> Y) = (* yY-3Y2 + 5x) ‘y = Пример 2. f (x, y) = x + y — Vx Find /; (3; 4). Решения. Сначала найдите частную производную функции f (.x, y) по _ Gx c , y) — ( + y-K ^ m1?); = (* ■ + //); — (- 1 + 0- + 1-J -2x-1-. . Затем вычислите частичное значение найденной частной производной на 3 или 4. , Пример 3. Разместите стержень на оси Ox. Температура 0 в любой точке M (x) на стержне является функцией координаты x () точки M и времени t: B = / (*, /). x — Для x0 функция E = * f (xott) представляет изменение температуры в данной точке на шкале как функцию времени t.
Частные деривативы ля В этот момент L указывает скорость изменения температуры со временем. Если здесь установить t = t0, функция 9 = / (*, t0) дает закон распределения температуры вдоль стержня в этот момент. 0 дБ в момент времени t0. В этом случае частная производная Скорость изменения температуры вдоль стержня в данный момент / 0. Как хорошо fy (x> y) = (* yy-3y2 5x) ‘y = Пример 2. f (x, y) = xy — Vx Find /; (3; 4). Решения. Сначала найдите частную производную функции f (.x, y) по _ Gx c , y) — ( y-K ^ m1?); = (* ■ //); — (- 1 0— 1-J-2x-1-. . Затем вычислите частичное значение найденной частной производной на 3 или 4. ,
Пример 3. Разместите стержень на оси Ox. Температура 0 в любой точке M (x) на стержне является функцией координаты x () точки M и времени t: B = / (*, /). x — Для x0 функция E = * f (xott) представляет изменение температуры в данной точке на шкале как функцию времени t. Частные деривативы ля В этот момент L указывает скорость изменения температуры со временем. Если здесь установить t = t0, функция 9 = / (*, t0) дает закон распределения температуры вдоль стержня в этот момент. 0 дБ в момент времени t0. В этом случае частная производная Скорость изменения температуры вдоль стержня в данный момент / 0.
Геометрический смысл частных производных функций двух переменных Рассмотрим геометрический смысл частичного дифференцирования функции двух переменных z => = f (x, y). Как известно, график функции y) является поверхностью. Рассмотрим точку P0 (x0; y0) на плоскости Oxu и соответствующую точку M0 (x0; y0; z0) на поверхности (рис. 219).
Переведите ось, начиная с точки 0X (0; y0; 0), и создайте плоскую кривую LM0B, полученную при разрезании плоскости новой координатной плоскостью OtXZ (то есть старой плоскостью системы координат y = y0) Я думаю. Эту кривую можно рассматривать как (график функции одной переменной r • — = »/ (*, y *)) в плоскости OxXZ (т. Е. В плоскости старой системы y = y0). Но согласно геометрическому смыслу функции одной переменной ^^ o) * = = «Tga, где a — угол с осью 0YXt или, что эквивалентно, касательная ось Ox, нарисованная на кривой AM0B в противоположных точках M0, G
Это тга. Так что стоимость частного производства ~ Точка P0 (x0; y9), равная тангенсу угла, образованного осью Ox Касательная к точке пересечения поверхности z = f (x, y) и плоскости y = tj0 в точке M0 (x0; y9 \ * 0). Это Геометрический смысл частичной дифференциации Точно так же, геометрическое значение частичной дифференциации 8. Частные производные высшего уровня
Частная производная функции нескольких переменных / ^ ss / является функцией одной и той же переменной / n> V. Эти функции могут иметь частные производные, и Y называется частной производной второго порядка по Y (или Частные производные219 Порядок оригинальной функции). Так, например, функция z — f (x} y) двух переменных имеет четыре частных производных второго порядка, определенных и отображаемых как ты дх д) ты Ay —fly 2 / ■ * V * ”yn ,, — / lgI *” Y) * Ду ду ду dh2 д * г до дх дх д. du dh = Гух (х> у); = фу * (X, Y). Сделать д (* делать) d * z __ p » du2 Функция с тремя переменными u- / (x, y y r) имеет девять частных производных второго порядка.
д (- \ д (- \ / ди \ \ dx) d2 и ξn. , v такие как Производные функций третьего и высшего порядка некоторых переменных определены и показаны аналогичным образом: n-е частные производные функций некоторых переменных d из переменных является первой хаотической производной (n — 1) -ой частной производной той же функции. Например, частная производная третьего порядка dxdyi функции z = f (xt y) является частной производной первого порядка по y. д * и
Частичное дифференцирование второго порядка: д * з , д (шц) Дх Дуг До Частные производные второго порядка или выше, которые наследуют несколько различных переменных, называются смешанными частными производными. Например, деривативы dlz frz dh (rg dx do * do do dx * dhdu1 1 dx du dx Является смешанной частной производной функции двух переменных z = f (x, y).
Пример. Найти смешанную частную производную второго порядка функции z = * x2y *. Решения. Найти первую частную производную 1 = 2 * 3 * | = 3 Затем найдите смешанную вторую частную производную д (* д (- \ d2g _ Vdu; _PhLGL ‘-fV // 2 dudh ~ dx- \ * xy) x-bx. Смешанные частные производные и Оказывается, единственное различие — это порядок дифференцирования, то есть порядок, в котором дифференцирование выполняется по разным переменным. Этот результат не является совпадением. Следующая теорема справедлива для смешанных частных производных, которые принимаются без доказательства. Теорема Две смешанные частные производные одной и той же функции отличаются только порядком дифференцирования и равны в условиях непрерывности. В частности, для функций двух переменных от z до f (x, y): дх = дх дх ду ~ до дх ‘

