Оглавление:
Частные производные
Функция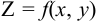 
называется непрерывной в точке 
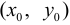, если она определена в этой точке и 
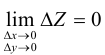, где 
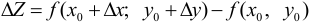— полное приращение функции 
.
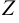Пусть задана функция 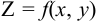и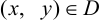 
. Если изменение функции 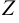происходит при изменении только одного аргумента, например 
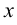, при фиксированном значении другого аргумента 
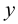, то функция получит приращение 
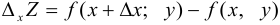, которое называют частным приращением функции 
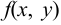по 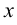, и мы приходим к функции одной переменной.
Если существует конечный предел:
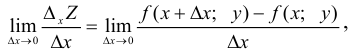
то он называется частной производной функции 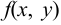по аргументу 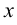и обозначается 
.
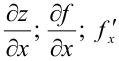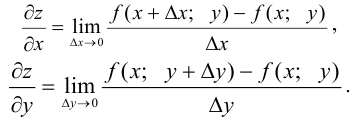
Задача №68.
Найти частные производные функции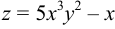 
.
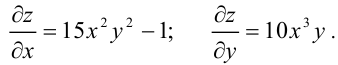
Аналогично вводятся частные производные для функций трех или большего числа переменных.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
