Оглавление:
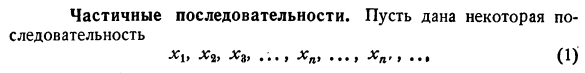



Частичные последовательности
Частичные последовательности. Давайте дадим некоторую последовательность ху-х * Х9、 •••> Икс ’л’>••• (1) Вместе с ним рассмотрим частичную последовательность, извлеченную из него Ч / С*•••»•••(2) Где{i *} последовательность возрастающих натуральных чисел. •••(3) Здесь роль числа, которое принимает все естественные значения строки, больше не l, но k \ nk-это функция k, которая принимает естественное значение и, по-видимому, становится бесконечной с увеличением k. Если последовательность (1) имеет определенный предел a (конечный или нет), то частичная последовательность (2) также имеет тот же предел.
Если последовательность (1) не имеет четкого ограничения, это не исключает возможности наличия ограничения в какой-либо частичной последовательности. Людмила Фирмаль
- Например, предположим, что xn =(-1) n+|;.Эта переменная не имеет ограничений. если l выполняется только с 1 нечетным или четным значением, то частичная последовательность −1, х% −1,•••, м••• И затем Х5 1) Х ^ • • * > 1 1• Есть ограничения, 1 или 1, соответственно. В случае неограниченной последовательности(1) может оказаться невозможным разделить частичную последовательность (2) с конечными пределами[сама последовательность(1) стремится к±oo]. Скорее, для ограниченной последовательности следующие утверждения принадлежат Больцано и Вейерштрассу
Лимонад Больцано-Вейерштрасс. Из ограниченной последовательности (1) всегда можно извлечь частичную последовательность (2), сходящуюся к конечному пределу. (Данная формулировка не исключает возможности получения числа, равного составу этой последовательности, что удобно при применении). Доказательство. Допустим, все числа xn окружены границами a и B. Если разделить этот интервал[a, b]пополам, то весь интервал[ar b]этих элементов содержит конечное число, поэтому по крайней мере половина содержит бесконечное число элементов в определенной последовательности.
- Это и есть impossible. So, [% , b ]будет половина 1, содержащая бесконечное число xn(или обе половины Такой, значит-любой из них). Аналогично, из интервала [a1 (b%], что половина[a9、Продолжая этот процесс, на этапе L выберите интервал[ak> bk], который также включает бесконечный набор чисел xn. It продолжается до бесконечности. Каждый построенный интервал (начиная со 2-го) включается в предыдущий интервал и занимает половину it. In кроме того, длина k-го зазора равна、 Б-а * Б 2К! Здесь мы приходим к выводу, что когда леммы применяются к вложенным интервалам[n°46], ak и t имеют тенденцию быть общими границами C.
Здесь, строительство частичную последовательность{xpk все \осуществляется индуктивно следующим образом: в качестве xn1, [а|, ВХ .для xn% используйте любой(например、 Как правило, в качестве xnk вы получаете один из элементов xn (первый, например), который будет включен после ранее выбранного xn1, xn%. [Ак, ьк].Возможность Такой выбор, который делается в свою очередь, обусловлен тем, что каждый интервал[aL, bk]содержит бесконечное число чисел xn>, то есть произвольно большое число элементов xn.
Получаем один из элементов последовательности, содержащейся в xn (например, первый). Людмила Фирмаль
- В дальнейшем、 Ак xlk ^ БК и\ \ так = \ МК = с、 Тогда, по теореме 3), η°38 и Пχ» k = su, если это необходимо. Метод, используемый при доказательстве этого утверждения и заключающийся в непрерывном делении половины рассматриваемого интервала, часто бывает полезен и в других случаях. Лемма Больцано-Вейерштрасса значительно упрощает доказательство многих трудных theorems. It это как если бы главная трудность обсуждения была взята. Используйте его в следующем выпуске.
Смотрите также:
Решение задач по математическому анализу

