Частичная замена переменной и сведение к системе

Частичная замена переменной и сведение к системе

Иногда, чтобы решить уравнение, прибегают к следующему способу. Вводят новую переменную (новые переменные), но при этом в уравнении оставляют и старую переменную (старые переменные). То есть не полностью переходят в уравнении к новой переменной, а частично. В результате решение уравнения оказывается сведено к решению системы уравнений. Может оказаться, что система решается легче, чем исходное уравнение. Именно в этих случаях и рекомендуется использование этого подхода.

Пример №199.

Решить уравнение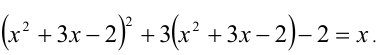

Решение:

Введём новую переменную, положив 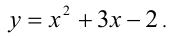Тогда, очевидно, уравнение равносильно следующей системе алгебраических уравнений

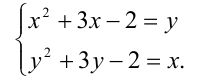
Решение этой системы относительно x будет решением исходного уравнения. Для решения системы вычтем почленно из одного уравнения другое и получим следствие

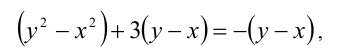
которое легко расщепляется на совокупность двух уравнений

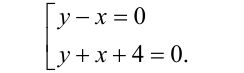
1) Подставляя у = x во второе уравнение системы, получаем квадратное уравнение 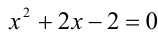, откуда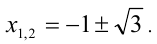

2) Подставим теперь во второе уравнение системы 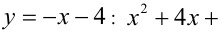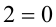, откуда находим 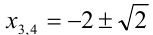. Объединяя, получаем ответ.

Ответ: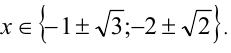

Пример №200.

Вычислить разность между максимальным и минимальным действительными корнями уравнения

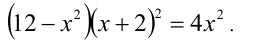
Решение:

Так как 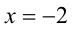не является корнем, то поделим на 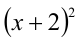и получим равносильное уравнение

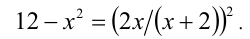
Сделаем замену 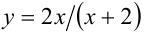, тогда уравнение равносильно системе

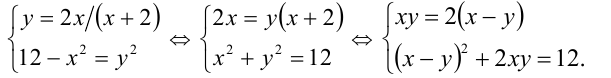
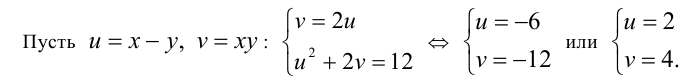
У 1 й системы нет решений, а из второй находим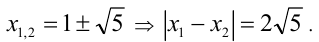

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Возвратные уравнения в математике с примерами решения

Тригонометрические подстановки с примером решения

Графический подход (метод координат) в математике с примерами решения

Рациональные алгебраические уравнения и неравенства с примерами решения