Оглавление:











Цепная линия
- Задание 13. 7. 30 метров гибкой нити и 7. 5 кг. Весь агрегат свободно подвешен на 2 опорах, расположенных на одном уровне на расстоянии возвратно-поступательного движения. Определите висячую стрелку в середине пролета и максимальное натяжение нити. Решение. Давайте набросаем положение равновесия yarn. In вопрос, расстояние между опорами. Длина всей нити g 3 м, вес единицы длины нити 5 7, 5 кг м.
Вот оно 2-й основной случай нагружения происходит, когда нить принимает форму цепной линии. Чтобы определить величину провисания нити f, необходимо составить уравнение для кривой равновесия нити. После выбора системы координат cx, как показано на рисунке, используйте основное дифференциальное уравнение 1, которое принимает следующий вид К заданию 13. 7. Функция азимутального — Длина дуги cd. Интегрируйте это уравнение и заранее выразите длину s как y. Используйте для этого хорошо известные Подставляя dyfdx из выражения 1, Вы получаете следующую форму Если мы интегрируем это уравнение — Арш с,. Вопрос п 2 Интегральная константа ci определяется из условий выбранной системы координат s 0.
После составления дифференциального уравнения движения (пункт 4) следует рассмотреть условие статического равновесия мате-риальпой точки, совершающей колебания. Людмила Фирмаль
Выражение 2 принимает вид 3 Подставляя эту формулу в Формулу 1, получаем следующую формулу Ферреневое уравнение кривой равновесия пряжи ды ш ДХ. После интегрирования, находим В если x 0, то координаты y-0, поэтому cr — h q и, наконец, Теперь у нас есть все уравнения, которые нам нужно решить problem. In факт, если задать Формулу 3 x z 2 Или после присвоения номера 112. 5, 56. 23 Это уравнение вида 2z shz.
Используйте таблицу гиперболических синусов, чтобы найти выбор ее решения Определить натяжение нити в точке 5, где h a 25, s4 кг. Искомая провисающая нить находится из Формулы 4 Если положить ее в x c2. Для определения натяжения нити используйте основное соотношение 2. Напомним, что q qs, применяя формулу 3, находим q f sh. Подставляя это в Формулу 2, получаем Или с помощью соединения 4 7 — я 4Р. Из последнего уравнения следует, что натяжение нити максимизируется в неподвижных точках a и b, где Гта я ФК 25. 84 7. 5-11. 94 115. 4 кг.
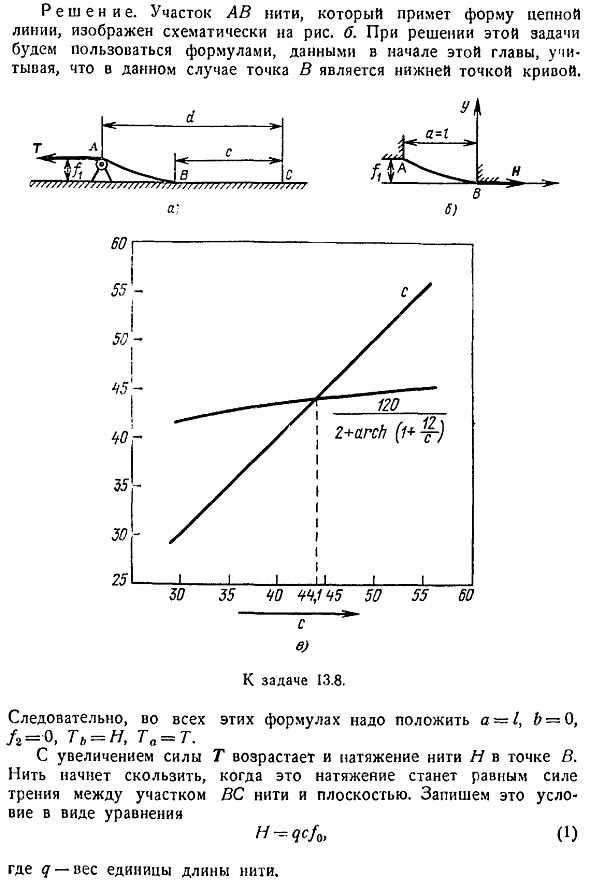
Задача 13. 8. Часть гибкой нити, равномерно распределенной по весу по длине, находится на горизонтальной плоскости. Остальные дачи проходят через небольшой блок а рисунок а. Постепенно увеличивая усилие t приложено к концам thread. In в этом случае длина линии контакта между ВС и плоскостью нити уменьшается и приближается к определенному пределу С, где нить начинает скользить вдоль плоскости.
Определить это предельное значение С, если d 60 м, l 6 м, а коэффициент трения между резьбой и плоскостью 0 0, 5. Другие способы решения такого уравнения см. В задаче 13. 8. Решение. На рисунке 2 показан участок av-потока, который принимает форму одной цепи. b. To решите эту задачу, используя выражение, показанное в начале этой главы, в котором точка b является нижней точкой кривой. С Задача 13. 8. Итак, для всех этих формул нужно разместить a-1, b-0, r 0, t h, ta t.
При увеличении силы Т натяжение нити Н в точке В также увеличивается, и когда это натяжение равно силе трения между частью ВС нити и плоскостью, нить начинает проскальзывать. Запишите это условие в виде уравнения Ч — qcfa, 1 Где d-вес единицы длины нити. Значение h должно удовлетворять формуле 14. В этом выпуске 2 Исключается из уравнения 1. 2 Значение h, получим следующее уравнение Из него определяется желаемый размер s. Быть l d-c. Уравнение эго Вот бы заменить знаменитые чудесные вещи 3 Вы не можете решить это трансцендентальное уравнение в отношении использования точных алгебраических методов. Поэтому, чтобы найти его корень, нужно воспользоваться приближенным методом.
Рассмотрим 2 таких ways. It это графический метод и итерационный метод. Графический способ заключается в создании левого и правого графика уравнений в 1 чертеже. Горизонтальная ось пересечения этих графиков показывает примерное значение маршрута. Для простоты сначала представим выражение 3 в следующем виде 120. 2 арка ий 4 График в левой части уравнения 4 является биссектрисой первой координаты angle. To постройте график правой стороны, вычислите значения некоторых значений в c, взятых рядом с расчетными значениями маршрута. Результаты расчетов сведены в таблицу. 1. 4 рефские. 4 2 арка 4 120 30 0. 4000 1. 4000 0. 8670 2. 8670 4186 35 0. 3429 1. 3429 0.
Если повторить этот процесс несколько раз, то можно получить значение корня с произвольной точностью, если f x 1 в интервале между корнем уравнения и первым приближением. Если это условие не выполняется, то уравнение должно быть преобразовано по крайней мере, путем передачи его в обратную функцию. Для 30 c 55 легко видеть, что модуль правой производной Формулы 4 меньше 1. Поэтому это выражение можно повторить, взяв значение c из заданного интервала первого приближения c0. C0 46 м. 120. 2 л 44, 3 м 44, 08 м 11a может завершить итерационный процесс, наконец, получив c 44. 1 m. Задача 13. 9. Гибкий поток без расширения приостанавливается от поддержки a и блока, который можно игнорировать.
- Вес q на единицу резьбы. Баланс определяет длину свободно висящей части нити, которая не нарушается. Третий блок игнорируется. Ты поешь. После выбора начальной точки самой нижней точки кривой, используйте уравнение 1, чтобы найти уравнение кривой. Где — напряжение в точке С. Тогда заметим, что вертикальное приращение нагрузки dq qds ды ЗДС Или заменить ДС У1 y 2 ДХ При разделении переменной Когда вы интегрируете ды И1 РТ 7г- с Для краткости укажите h q a. Как, о Тогда ci 0 и, наконец, выражение 2 имеет вид Г У1. Из Формулы 3 Вы можете легко проверить, умножив 3 на 4.
При добавлении выражений 3 и 4 Если мы интегрируем последнее уравнение если x 0 и y 0, то перенос начала координат 5 записывается в виде Точка o 0, — a. Ось ox называется основанием цепной линии. Это связано с тем, что я держусь только под действием вертикальной нагрузки, поэтому горизонтальное натяжение не изменяется. T h, или t h c- Согласно 1, это равенство может быть переписано в следующем виде 1 2 3 Ноль 5 1 равна Проекция Если вычесть равенство из 3 в 4 И, наконец, получить свободную точку кривой Натяжение нити по формуле Северный t — y1 chu1- В результате, если длина подвешенной части равна yt bd, то нить будет находиться в равновесии. Задание 13. 10.
При составлении дифференциального уравнения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты. Людмила Фирмаль
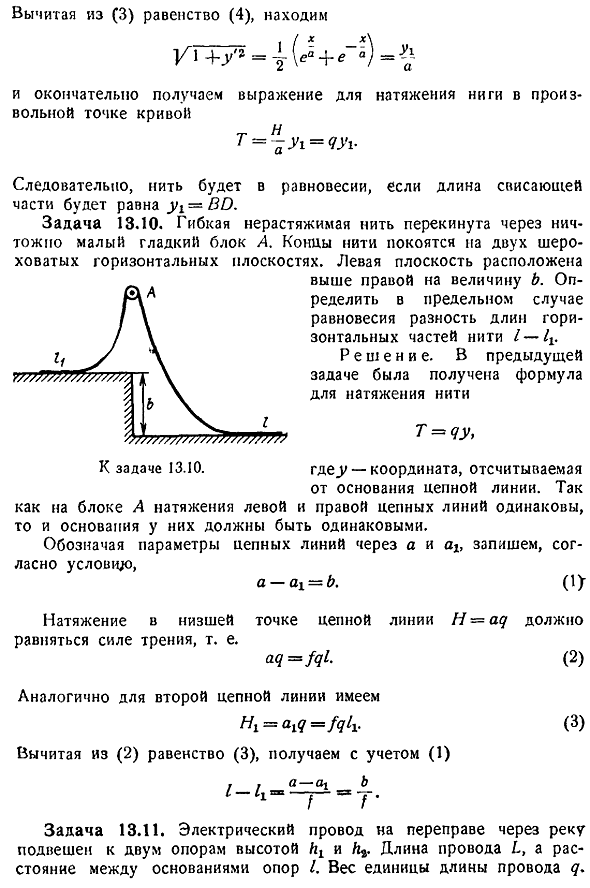
На небольшой и гладкий блок набрасывают гибкую, не натянутую нить. Нить лошади находится на 2 грубых горизонтальных плоскостях. Левая плоскость находится выше правой плоскости на величину b. In в предельном случае равновесия определяют разность длин горизонтальной части нити 1-1. Solution. In в предыдущем выпуске была получена формула натяжения нити Т Тип qy где y-координаты, измеренные от основания цепной линии. Правая прядь такая же Основа для этого должна быть одна и та же. В зависимости от условий, a и write указывают параметры линии цепи а-АИ б. 1 г, г Вопрос 13. 10. Для Как блок а в левом напряжении Натяжение в самой нижней точке цепной линии h aq должно быть равно силе трения.
Аналогично, для 2-й цепной линии 3 Если вычесть равенство 2 из равенства 3, то вы принимаете во внимание 1 Я Задание 13. 11. Проволока на пересечении реки подвешена к 2 столбам по высоте и c. Длина проволоки равна l, расстояние между основаниями опор равно i. Вес q на единицу длины проволоки. Для bx 30 м, b2 12 л, 20 м, 1 45 м, q 1. 25 кг м найти уравнение кривой, максимальное провисание и максимальное натяжение. Решение. Если выбрать начало координат в верхней части цепной линии o, то в соответствии с 10 уравнение кривой имеет вид В данном случае неизвестно следующее. Положение точки o, определяемое отрезком, также является горизонтальным натяжением n.
В определении используется выражение, определяющее условия прохождения цепной линии через точки соединения А и В, а также длину провода между опорами. У нас есть 2 НТ-н0 ч 1 3 Найти более длины провода В1 г ДХ г л ш ДХ х функции rfx 7shff e в sh4r shff 2 st, cht 4 От 2 до 3 Чтобы определить горизонтальное натяжение n, возьмем 4 и 5 2, Затем возьмем 2 и вычтем от 1-го до 2-го 4 Из этого уравнения 1д 2Н В Р П 2. 06 К1 2Н это трансцендентальное уравнение вида shz 2.
Графически решается с помощью fi z shz, g g 2. 06 z, которое создает или аппроксимирует 2 кривые в соответствии с таблицей. Их пересечение дает r 1d 2ч 2. 22, оттуда 6 4, 48 −1, 25 6, 6 кг. Чтобы найти a, разделите 5 на 4. У нас есть Откуда Учитывая 6, остается найти d0 из 2 Найти уравнение кривой, подставив значения, найденные в уравнении 1 Приступайте к решению о провисании самого большого провода. Максимальная слабина — это точка кривой, где касательная линия кривой параллельна линии ab. Из этого уравнения находим абсциссу искомой точки кривой Самые большие провалы Макс-е- а-xif по-Хо-у ХВ Т Н1 — ч дж а-х — н л- ч я-л педагогика 18. 74 м.
И согласно напряжению провода 7 l h a h 4 d1-l0 40, 5 кг, tb h qft h q h2-h0 m, 8 кг. Задание 13. 12. Цепь с равным сопротивлением представляет собой цепь переменной толщины, где толщина каждой точки пропорциональна напряжению t. in такая цепочка, вероятность обрыва во всех точках одинакова. Уравнение кривой равновесия и закон изменения толщины цепи определяются. Решение. Буква О обозначает переменный участок цепи, изменяющийся по ее длине. Если вес единицы объема цепи равен p, а ее длина равна s, то вес элемента ds равен puds. Выберите начало координат в самой нижней точке цепочки. Используйте уравнение 1, чтобы найти уравнение кривой 2 ДХ П О Где h-натяжение самой нижней точки цепи.
Приращение вертикальной нагрузки составляет rfq pa ds, и мы видим, что натяжение цепи согласно условию пропорционально толщине, то есть равно Т ka, k коэффициенту пропорциональности. При вычислении разности с обеих сторон уравнения 1 2 С другой стороны, проекция горизонтального натяжения оси x является постоянной величиной, так как на цепь действует только вертикальная нагрузка Ч Т — АО — const и Откуда 3 значение o вводится в Формулу 2. А потом мы это выясним. Здесь рассматривается ds j l dx.
Когда вы отделяете переменную, она выглядит так ды Ю Д Когда вы интегрируете arctgy г интернет. Происхождение выбран в самой низкой точке, где кривая сводится к минимуму. Так, если x 0, г 0, С1 0 4 диджей тг — xdx. Интеграция и поиск у — Линкос — х ХС. Если x 0, y 0, c2 0. — y lncos — — х, э к Кос- — х Или наконец-то е со −2-х 1. Это уравнение сопротивления curve. To найти закон изменения толщины цепи, используя уравнение 3.
Смотрите также:
Предмет теоретическая механика

