Центральные силы

Центральные силы

• Фигура равновесия представляет собой плоскую кривую, плоскость которой проходит через пересечение сил. Момент напряжения в этом отношении постоянен. Эти операторы можно рассматривать как результат аналогичных операторов, установленных для канатных полигонов, но они задаются непосредственно. Мы обнаружили, что если момент силы на оси F всегда равен нулю, то момент напряжения на этой оси постоянен. Внешние силы пересекаются в одной точке, поэтому, пожалуйста, используйте этот пункт в качестве origin.

Величинами к и р можно распорядиться таким образом, чтобы этот момент равнялся нулю, и тогда указанные четыре силы будут находиться в равновесии. Людмила Фирмаль

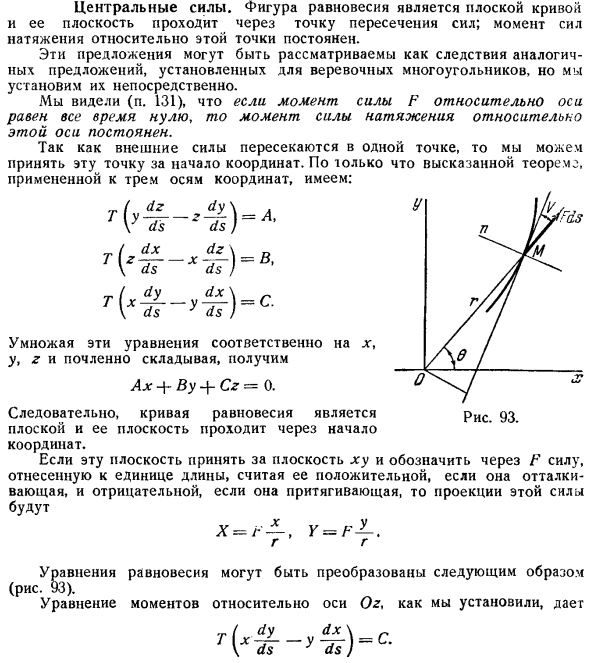
Теорема, которую мы только что упомянули. При применении к 3 осям, это выглядит так: Г р 1 г Если вы умножите эти уравнения на x, y и z соответственно и добавите термины для каждого из них, вы можете использовать 0 Ah f by Cz =0.Z7i В результате кривая равновесия становится плоской, и ее плоскость проходит через головку фигуры. 93. Координирует. Если взять эту плоскость в плоскости xy и обозначить через F силу, относящуюся к единице длины, если считать ее положительной в случае отталкивания и отрицательной в случае притяжения, то проекция этой силы выглядит так: Х = р, г = Ф. Г Уравнение равновесия можно преобразовать следующим образом рис. 

• Как мы установили, уравнение момента на оси Oz выглядит следующим образом: ДТ х ДХ г ду В. Введем полярные координаты r и 0, чтобы свести эти уравнения к виду Tr = C, dT + Fdr = 0. дс Самый простой случай когда F является функцией вида r. тогда существует первый Интеграл, который может быть легко found. In факт, так как сила F очень потенциальна, T приобретается с использованием квадратуры г T = J f r dr Л= Г г. Иди. С помощью силы натяжения легко найти дифференциальное уравнение равновесия curve. To для этого подставьте значение T в первое выражение. Тогда у вас есть следующий формат р р в J0 = ЦРФ. Это уравнение интегрируется в квадратурах. Конечно. ДС = д р 4 г БД.

Отсюда следует, что главный момент равен нулю, так как он не может быть перпендикулярен всем образующим одной и той же системы гиперболоида, поскольку последние не параллельны одной и той же плоскости. Людмила Фирмаль

Подставляя это уравнение в уравнение предыдущих 2 степеней и решая его относительно tfO, получаем уравнение кривой. С врачом Иди. Например, если вы поместите F k где k константа Р = Ф р = е Уравнение кривой включает в себя эллиптический Интеграл. Однако, если вы присвоите значение t = КР к 0 в силу Т кривой необходимо будет ИСО гиперболы вокруг точки 0. Естественное уравнение. Пусть V угол между касательной нити и продолжением радиус вектора OM. Расстояние от полюса O до касательной равно R sin и рис. 93.Условие, что момент напряжения постоянен Гг грех В = С Кроме того, если вы пишете, что проекция силы F на Нормаль равна G p, Р грех в=.

Смотрите также:

Решение задач по теоретической механике

Параллельные силы	Пример существования бесчисленного множества положений равновесия
Определение постоянных	Равновесие нити на поверхности