Оглавление:







Центральное растяжение прямого бруса. Напряжения
- Центральный участок прямых стержней. Напряжение Центральное растяжение или сжатие-это вид деформации, при котором в любом поперечном сечении балки присутствует только продольная (вертикальная) сила Af, все остальные коэффициенты внутренней силы равны нулю. Явление Центрального натяжения (сжатия) возникает только тогда, когда все внешние нагрузки действуют на ось, проходящую через центр тяжести поперечного сечения балки.
Например, центральное натяжение испытывает трос башенного крана от веса поднимаемого груза. Если внутренняя сила W направлена от сечения (соответствует растяжению), то она положительна, а если она направлена к сечению (соответствует сжатию), то отрицательна. Если направление силы W неизвестно, она всегда должна принимать положительное значение. Если после решения уравнения сила N получается со знаком плюс,
то балка в этом сечении растягивается и сжимается со знаком минус. Людмила Фирмаль
Рассмотрим прямой бар. 15.1, а) постоянное и симметричное поперечное сечение, строго закрепленное сверху и нагруженное тремя внешними концентрическими L=Yu kN, F2=20kN, VZ=30kN, приложенными в точках B, C, D и направленными вдоль его продольно ориентированной оси. Естественно, что на разных участках длины балки будут возникать различные по величине внутренние продольные силы. В этом вопросе есть три таких участка: солнечный участок, CD-участок и DK-участок. Чтобы найти
внутреннюю продольную силу N, мы используем метод сечений. То есть внутри всех трех секций БК, КД и ДК отбросить любую из частей и заменить ее влияние на левую часть неизвестной внутренней силой N.- 134 * г) Но) Рис 15.1 Правление. Давайте перейдем к решению нашей проблемы. Раздел 1-1. Разрежьте балку сечением 1-1 на две части, отбросив одну из них, например, верхнюю. Для упрощения расчета необходимо отказаться от той части, в которой действуют дополнительные внешние силы. В этом случае на верхнюю часть воздействуют три силы, поэтому удобнее выбросить ее и
- оставить нижнюю часть. Предполагая последнее растяжение, которое заменяет действие отброшенной части неизвестной продольной силы, получаем схему (рис. 15.1, б). Составим условие равновесия левой части пучка: S Z=jVi-10=0, где n = 10kN. Таким образом, мы видим, что сила постоянна на всем участке BC, так как независимая переменная z не входит в уравнение равновесия. 2-2. Чтобы определить продольную силу^2 в любом поперечном сечении, 2-2 идут точно так же, как и предыдущий (рис. 15.1, б). Составим уравнение равновесия: SZ= / V2-10-20=0, W2=30kN. Раздел 3-3. Для определения продольных сил сечения 3-3 целесообразнее оставить
верхнюю часть, но необходимо было определить реакцию с жесткими опорами. Мы его не нашли, поэтому оставим нижнюю часть(рис. Уравнение равновесия записывается в виде SZ=Ws 15.1, g)—10— —20—30 = 0, где м3=60кн. Для наглядного отображения изменения характеров (законов) в любом из внутренних силовых факторов 135 график изменения длины стержня этого коэффициента состоит в том, что горизонтальная ось соответствует положению сечения на оси, а вертикальная ось указывает значение исследуемого коэффициента этого сечения. Это называется графом. Перейдем к построению графика продольных сил данной балки. В этом случае
балка содержит три секции, поэтому для построения графика необходимо отдельно изучить изменение продольных сил каждой секции. Из уравнения Людмила Фирмаль
равновесия определим величину LA1=1o kN сечения ВС, чтобы величина не изменялась в этом сечении, то есть N1=10kN всюду, 1—/сечение следовательно, график продольной силы w i в первом сечении постоянен. В постоянном токе переменная z не входит в уравнение равновесия, поэтому закон изменения на вертикальной оси также постоянен. Участок этого участка отличается по размерам от участка первого, так как м2=30 КН. В сечении DK закон изменения продольных сил ЛГЗ также становится постоянным (м3=60кн). Чтобы построить график вертикальной силы N на данном стержне, нарисуйте прямую линию, параллельную оси стержня, и, перпендикулярно ей, нарисуйте фигуру вертикальной силы на определенном масштабе величины, которая возникает в
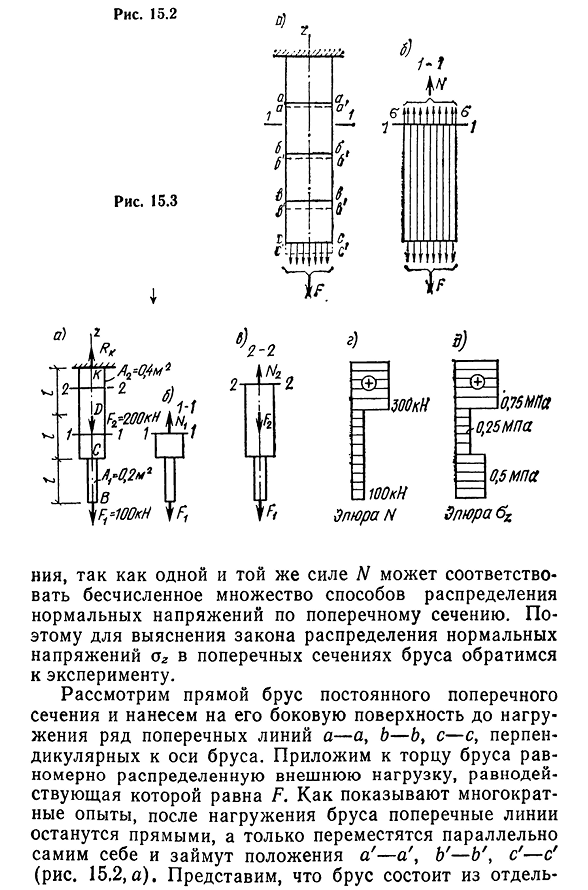
соответствующем поперечном сечении стержня. 15.1, д. Пусть переходят от центрального натяжения (сжатия) к определению нормального напряжения на поперечном сечении прямого стержня. Центральное натяжение поперечного сечения стержня имеет только продольное растягивающее (или сжимающее) усилие W нормального давления az, в результате распределенное по всей площади этого сечения. Таким образом, для любого поперечного сечения связь между напряжением O2 и результирующим N может быть описана в следующем виде: Да (15.1) Однако из этой формулы невозможно найти закон распределения нормального напряжения в области сече- 136 страница 15.3 Рис 15.2 y-, / в Пять. Один. — г) С) Потому что одна и та же сила N может справиться с бесчисленными способами
распределения нормальных напряжений по поперечному сечению. Поэтому для выяснения закона распределения нормальных напряжений в поперечном сечении балки эксперимент был перенесен. Рассмотрим прямой брус определенного поперечного сечения, а перед загрузкой ряд горизонтальных линий А-А, Б-Б, В-С, перпендикулярных оси бруса, положим его на бок. После нагружения поперечная линия балки, как показали повторные эксперименты, остается прямой, но движется параллельно самой себе, располагаясь a’ — a’, B’-b’, o’ — C'(рис. 15.2, а). Допустим, балка состоит из частей- Тонкий вертикальный призменный элемент с площадью 137 dA (рис. 15.2, 6). Поскольку все поверхностные продольные элементы имеют одинаковую длину, можно предположить, что все внутренние продольные призматические элементы имеют одинаковую длину.
После этого любое поперечное сечение балки остается плоским после деформации, перемещаясь параллельно исходному положению, т. е. плоскому сечению до деформации. Таким образом, при Центральном растяжении (сжатии) прямого стержня выполняется гипотеза GI: плоского сечения (гипотеза Бернулли). Так как одна и та же деформация растяжения соответствует одному и тому же нормальному напряжению SGG, то балка становится постоянной во всех точках поперечного сечения нормального напряжения. Тогда при o2=const отношение между V и oz принимает следующий вид N=az[dA=(Jz), (15.2) Но Так… vz- / V / A.(15.3) таким образом, в поперечном сечении балки при Центральном растяжении или сжатии нормальное напряжение oz, которое равномерно распределено равным отношению внутренних продольных сил к
поперечному сечению, предполагается, что нормальное растягивающее напряжение является положительным, а сжимающее напряжение-отрицательным. Приведенное доказательство равномерного распределения нормальных напряжений в поперечном сечении стержня выполнено в предположении, что внешняя нагрузка, приложенная к торцу стержня, распределена равномерно. Рассмотрим другие способы приложения внешних сил к концам балки,например, форму концентрации или некоторую концентрацию. В случае приложения такой внешней нагрузки гипотеза о плоском сечении вблизи места приложения внешних сил оказывается несостоятельной. В местах приложения сосредоточенных сил сечения сильно искривлены, что приводит к появлению больших локальных напряжений и деформаций. Однако на некотором
расстоянии распределение нормальное, приблизительно равное линейному размеру поперечного сечения от места приложения концентрации Напряжение секции 138 равномерно выравнивается, приближаясь. Быстрое снижение локального напряжения при удалении от точки приложения сосредоточенной силы было исследовано Сен-Венаном и названо его именем. Согласно принципу Сен-Венана, на участке, достаточно удаленном от места приложения внешней нагрузки, напряжение практически не зависит от фактического способа приложения этих нагрузок, а зависит от результата. Примером может служить случай с клещами, которые при разрезании сминают небольшой участок проволоки. На самом деле, независимо от того, насколько велика сила давления, создаваемая нажатием на клещи (результат равен нулю), на
остальной части провода почти нет напряжения. Изучение закона распределения напряжений в областях, близких к месту приложения, является специальной задачей, которая изучается в курсе теории упругости. Локальные напряжения возникают даже в месте резкого изменения поперечных размеров балки, в балке со ступенчатой балкой или отверстием. Фактические расчеты обычно не учитывают локальные напряжения (если только эта проблема не исследуется специально), но нормальные напряжения учитывают, что они равномерно распределены.、 Для того чтобы построить нормальный график напряжений-аз, необходимо визуализировать характер изменения силы вертикальных напряжений в различных сечениях по длине древесины, то есть определить интенсивность напряжений.、 Например. Для древесины (рис. 15.3, а) участок W и O2. Решение. Сначала рассчитайте величину внутренней продольной силы N.
Смотрите также:
Решение задач по технической механике
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

