Оглавление:


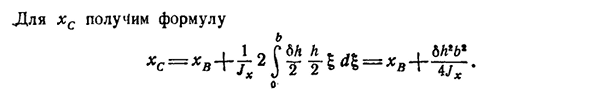

Центр изгиба
- Центр изгиба. Предположим, что поперечное сечение стержня асимметрично. То, что сила, действующая на любую плоскость, проходящую через эту ось, не вызывает скручивания, указывает на то, что существует ось, параллельная оси стержня.
Точка пересечения этой оси с плоскостью сечения называется центром изгиба. Если есть такая точка С, то касательность сечения стебля, точка. Таким образом, КС
всех тангенциальных сил на расстоянии до точки с равен нулю. Людмила Фирмаль
Элемент ds с координатами x, y подвергается воздействию силы rb d s (рис. тельно есть точка Это привело к переездам. Весеннее равноденствие через Это、 Ряса, 192. 192); момент, к которому она относится- ТБ ДС п, Где p-длина перпендикулярной линии, которая проходит от точки C до касательной. Если C-центр сгиба、 л Дж МДП
ДС=0. Отчет Однако p d s-это удвоенная область треугольника с основанием ds и вершинами точки C. И так оно и есть., J TB ds=0,280 изгиб и кручение тонкостенных стержней Применим формулу интегрирования частей. Возьми: Л Отчет Но t исчезнет при s=0 и y=Y.
- воспользуемся также уравнением (126.2) для преобразования интеграла. С д (ХВ)_ds Как показано в § 126. Конечным результатом будет:/. И положение изгибающего центра определяется следующим образом, так как он является необязательным с Og- И На него распространяются следующие условия: * (1 2 8 С У l3Jm г — ^х б д с=0.
Я Л, $ Отчет Очень основным является Центр изгиба углового профиля. Если J принимает вершину за полюс, то условие (128.1) выполняется, так как secto-’равно нулю.- Евро Рис 193 Реальная область находится в центре, а вершина-в центре сгиба (рис. 193). Аналогично, для Т-образного сечения центр изгиба находится на пересечении стены с выступом. Заметим, что в выражении (128.1) любая константа может быть добавлена к значениюds=>J yabds, 0, 0, 0, 0. оси x и y считаются центрами, так как статический
момент площади поперечного сечения относительно оси x равен нулю Людмила Фирмаль
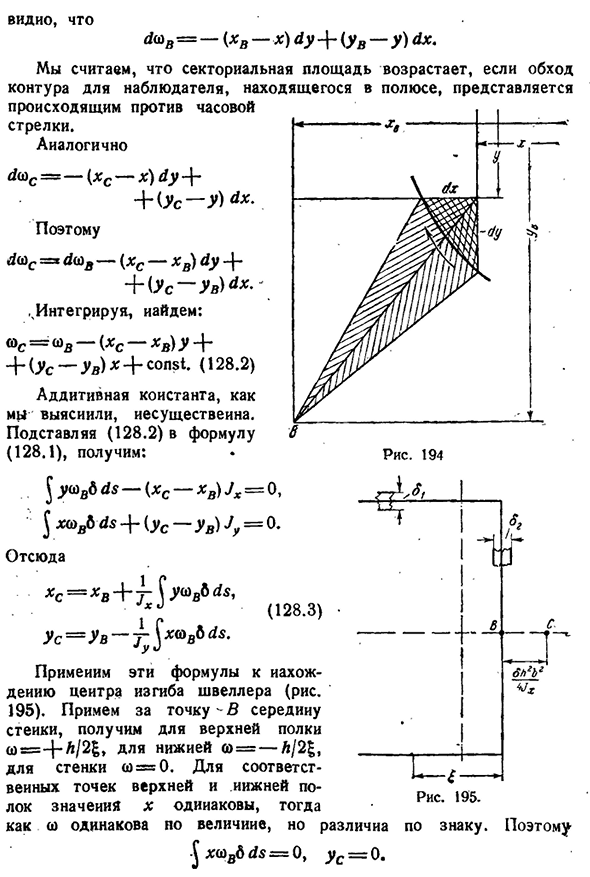
. В результате этого замечания площадь сектора профиля может быть подсчитана не с конца профиля, а с любого из них. Промежуточная точка. Чтобы действительно найти центр изгиба, важно иметь формулу, которая непосредственно определяет его координаты. Для этого возьмем любую точку B и примем ее за полюс сектора региона AB. Установим связь между СХС и рис. Сто девяносто четыре!- 8§ 128J Это можно увидеть Центр Сгиба 281 Д>Б= — {ХВ-х)г г — {- (г с) дх. Если байпасная цепь для наблюдателя, расположенного на полюсе, кажется происходящей в направлении против часовой стрелки,
область сектора считается большей. Также ЦАП—(ХС-х)г г — \ — +(МК-г^х — Так что d® БТ>ДС. Примените эти формулы к действию центра изгиба канала(195). Возьмем для этого ЧКУ-с серой; стены, получим для верха n<o)= — / — th/2|,<b= — h под стеной W=0. Для соответствующих точек верхнего и нижнего положений значения x одинаковы, а W одинаковы по величине, но различны по знаку. Отсюда * Jxo) Bdds=0,, us=0.-282 изгиб и кручение тонкостенных стержней[гл. HG’ D La x s получаем формулу Отчет I6L ’6′
Смотрите также:
| Нормальные и касательные напряжения при изгибе | Дополнительные напряжения при кручении |
| Касательные напряжении при изгибе в плоскости симметрии | Закон секториальных площадей |

