Оглавление:



Брусья некруглого сечения
- Весь изгибающий момент и боковые силы в сечении разбиваются на составляющие вдоль главной оси сечения: Mu, Mg, Qy, Qz. Нормальное напряжение от каждого изгибающего момента и тангенциальное напряжение от каждой поперечной силы и крутящего момента определяются соответствующим уравнением.
Алгебраическая сумма геометрической суммы нормального напряжения и тангенциального определяется для точки пересечения, где напряжение от каждой внутренней силы является наибольшим. Согласно полученному напряжению, уменьшение напряжения
ОПР определяется в соответствии с одной из теорий прочности. Расчет Людмила Фирмаль
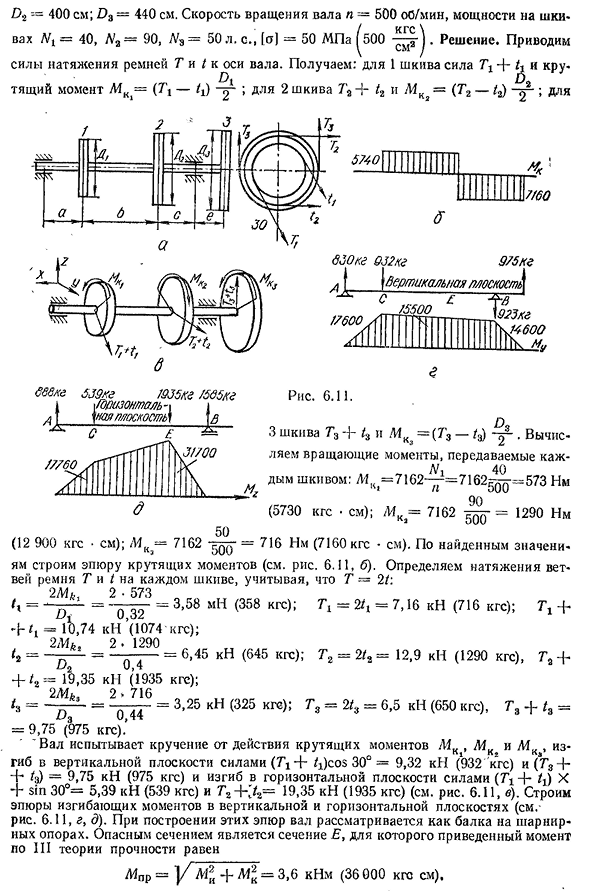
основан на условиях прочности, которые обычно регистрируются: Пример °PR [°]•(6.31). Определите диаметр вала ременной передачи (рис. 6.11) о третьей теории прочности. Данных; Я=200 см; б=400см; с=200см; д=150см; Д±=320см; 167D2=400см; да=440cm. Частота вращения вала n=500 об / мин, усилие шкива Nt = 40, N2=90, Ng=50 л. с., [o]=50 МПа^500дж. решение. Привод натяжения ремня t и t к оси вала.
Получаем: 1 шкив силы Ti+th и CRU- D2 Крутящий момент L4C=(Tg- / h); для 2 шкива 72+ / 2I=(T2—/2)>для Семнадцать тысяч шестьсот vzokg062kg975kg ■Я 923 километра—J4600 Но I \ вертикальная плоскость~Q£,’ …. ^-15500 ′ oosc л ^PPPSHP W г Фитти. Рис 6.11. 3 шкива T3-N z и MKZ=(r3 — /3) -. Рассчитайте крутящий момент, передаваемый
- каждым дымовым шкивом Ni40:L1K1=7162-=7162edd — =573Nm90 (5730kgfcm); MK=7162DRD — =1290Nm(12 900kgf•cm); M-71625q» — 716Nm(7160kgf•cm). По найденным значениям строим график крутящего момента (см. рис. 6.11, 6). Определите натяжение ремня ветви T и t каждого шкива, придав ему T=2t: = .2_|/? =з 58 млн (358kgf); 7’1=2/т=7.16 кн(716kgf); 7+ Н.=10.74 до n’(1074kgs); 2М, 2. 1290/2= — d — = — =6,45 кн(645 кг); T2=2 / a=12,9 кн( 1290 кг), T2+ 4 — /2 = 1^,35 kN
(1935KGE); ta==—d’»=3,25 kN (325kgf); TJ=2/3=6,5 kN (650kgf); T a-J-ta= = 9,75(975kgf). ’V al испытывает кручение от действия крутящего момента M K, L4K и L4ka и изгибается в вертикальной плоскости силой (?). i+ / Jcos30°=9,32 кн (932 кгс) и(7’3 + + /3) = 9,75 усилие в кн (975 кгс) и в горизонтальной плоскости (T±+/x) X+sin30°=5,39 кн (539 кгс) и T2-\’изгиб по J2=19,35 кн (1935 кгс) (см. Рисунок). 6.11, б). Построить график изгибающего момента на вертикальной и горизонтальной поверхностях (см.-рис.). 6.11, г, г).
При построении этих участков вал рассматривается как балка на шарнирной опоре. Людмила Фирмаль
Опасным участком является участок Е, и данный момент по теории прочности iii равен МПР=] / +=3,6 кНм(36000 кгс см). Диаметр вала 168then 3 / 32 • 36 000 -сказал он.. U3,14-500 — 9 −0 4 см< / d=9 см. Например. Растягивающее усилие P=228kN (628kgf) и крутящий момент l4k=42,7 Нм (427kgsssm) напряжения рассчитаны согласно III теории прочности для стержня круглого сечения d-диаметром 2 см (6.12). Решение. Нормальное напряжение одинаково для всех сечений и равно P4 * 628 3.14 * 22 200 кг / см2 (20 МПа). Касательное
напряжение вдоль максимального профиля профиля 16, 472. Т= _ ^Л= __ Пр3. 14 ″ 2®300 кг / см2 (30 МПа). На контурах опасного участка будут лежать все точки. Напряжения, рассчитанные в соответствии с III теорией прочности в этих точках, выглядят следующим образом: o=o1P RAE и т. д.= )/2 0 0 2 + 4. 3002=633 кгс / см2 (63,3 МПа).
Смотрите также:
| Ядро сечения | Основные предпосылки |
| Расчет бруса круглого сечения | Напряжения при чистом изгибе плоского кривого бруса (м 0, n = 0, q = 0 ) |

