Оглавление:






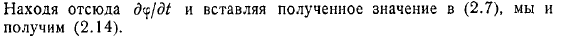

Безвихревое движение
Если в каждой точке поля скоростей движущейся жидкости нет вихря, т. е., следовательно, скорость является потенциальным вектором, то основное уравнение движения имеет вид. В этом случае потенциал скорости следует рассматривать как функцию от аргументов, так как движение может быть неустойчивым. Очевидно, что при выполнении движения во времени в каждой точке поля скоростей движущейся жидкости нет вихря гидромеханики. Нет вращения, и поэтому скорость является потенциальным вектором град, поэтому если вектор скорости град, тогда основное уравнение движения. в главе упрощается и принимает вид.
В этом случае потенциал скорости следует рассматривать как функцию от аргументов, так как движение может быть неустойчивым. Очевидно, град. Тогда из уравнения получаем. В случае несжимаемых однородных жидкостей, начиная с, выполняется очевидная зависимость. Для сжимаемых жидкостей аналогичное соотношение может быть установлено, когда жидкость. в этом случае вы можете повторно ввести установившееся движение обозначение или при сравнении коэффициентов производной аргумента их соотношение. Явно является частным случаем, поэтому для рассматриваемого невращательного движения формула принимает вид.
То есть в этих случаях массовая сила должна быть потенциальным вектором. Выражая поте силы как, град, сводим уравнение движения. к виду град. Тогда из уравнения. получаем. В случае несжимаемых однородных жидкостей, начиная с, выполняется очевидная зависимость. Постоянная для всех точек поля заключенное в скобки выражение не зависит от координат функция времени только указывает, что его форма остается произвольной. Интеграл этого уравнения движения называется интегралом коматита..
Если на границе некоторой односвязной области вихревое движение совпадает с безвихревым, то кинетическая энергия безвихревого движения в рассматриваемой области меньше кинетической энергии вихревого движения. Людмила Фирмаль
Если существует только гравитация, интеграл Коши получается в следующем виде для несжимаемых жидкостей, грааль Коши также получается в следующем виде для последнего случая полное решение задачи определения вихревого движения несжимаемых жидкостей, уравнение Лапласа, граничные условия и начальные условия течения определяются из фундаментального вида любой функции определяется, если временная зависимость в точке поля задана в Вперед. Движущиеся системы координат при рассмотрении абсолютного движения жидкости основное уравнение движения может быть описано во й главе формата.
Выпускники предположим, что абсолютное движение жидкости является зондирующим, то есть невращающимся. Далее, если предположить, что сила имеет потенциал, а плотность является функцией давления, то повторим вышеприведенный аргумент так, чтобы вид интеграла равновесия. Скорость движения системы возы вой. проекция на ось системы координат, а, это проекция на ту же ось вектора угловой скорости вращения движущейся системы установившегося безвихревого движения координат О. этот результат также может быть получен непосредственно. Формулы.
Последняя формула имеет фиксированную систему координат и производную, полученную с помощью вычисляется в подвижной системе координат, то есть всегда связана с подвижной системой координат, если точка относительно для последней координаты является функцией, и является производной от функции времени. Определяет проекцию переносной скорости. Итак, предполагая, что постоянны, по правилам дифференцирования комплексных функций, отсюда найти и вставить полученное значение получим.
При движении баротропной идеальной жидкости под действием потенциальных сил циркуляция скорости по замкнутому жидкому контуру не изменяется. Людмила Фирмаль

