Бесконечно убывающая геометрическая прогрессия с примерами решения

Бесконечно убывающая геометрическая прогрессия

а) Геометрическая прогрессия, знаменатель которой удовлетворяет условию 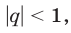называется бесконечно убывающей.

б) Суммой бесконечно убывающей геометрической прогрессии 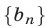называется предел S последовательности 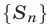, где 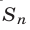— сумма первых n членов этой прогрессии. Эта сумма выражается формулой

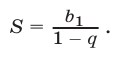
Примеры с решениями

Пример №31.

Найти первый член и знаменатель бесконечно убывающей геометрической прогрессии, если сумма этой прогрессии равна 4, а сумма кубов ее членов равна 192.

Решение:

Пусть 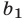— первый член, 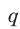— знаменатель, 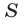— сумма прогрессии, 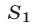— сумма кубов ее членов. Тогда

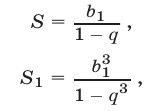
откуда

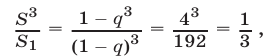
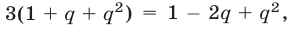так как 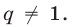Полученное уравнение, записанное в виде 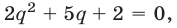имеет корни 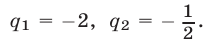Первый корень следует отбросить, так как 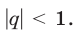Следовательно,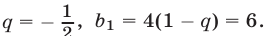

Ответ.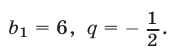

Пример №32.

Найти сумму бесконечно убывающей геометрической прогрессии, если ее второй член, удвоенное произведение первого члена на четвертый и третий член являются последовательными членами арифметической прогрессии с разностью, равной .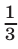

Решение:

Пусть 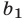— первый член, 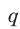— знаменатель, 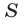— сумма бесконечно убывающей геометрической прогрессии. Тогда

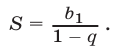
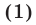
По условию,

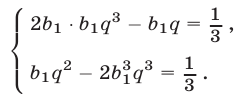
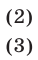
Складывая уравнения (2) и (3), получаем 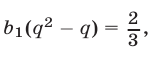откуда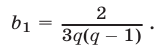

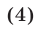
Подставляя выражение (4) для 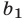\ в уравнение (2), получаем уравнение 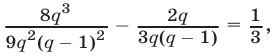которое можно преобразовать к виду 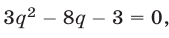откуда 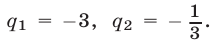Так как 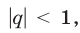то 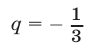и из (4) находим 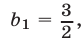а из (1) следует, что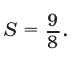

Ответ.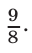

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Геометрическая прогрессия с примерами решения

Предел последовательности с примером решения

Определения синуса, косинуса, тангенса и котангенса угла с примером решения

Зависимость между синусом, косинусом, тангенсом и котангенсом с примером решения