Бесконечно малые и бесконечно большие функции
Функция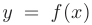 
называется бесконечно малой при 
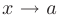, если для любого положительного числа 
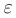найдется такое положительное число 
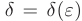, что для всех 
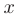, удовлетворяющих неравенству 
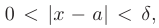выполняется неравенство 
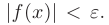. В более компактной форме это можно записать так:
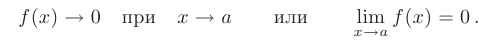
Например, функции
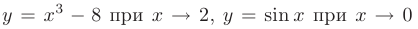
являются бесконечно малыми.
Определение бесконечно малой функции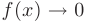 
при условиях:
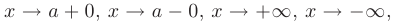
строится аналогично.
Основные свойства бесконечно малых функций:
- Алгебраическая сумма конечного числа бесконечно малых функций
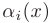есть бесконечно малая функция:
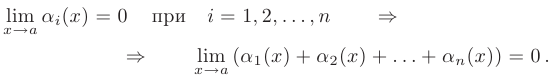
- Произведение на ограниченную функцию
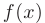(в т.ч. на константу или другую бесконечно малую) бесконечно малой функции 
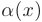есть бесконечно малая функция:
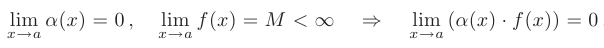
- Частное от деления бесконечно малой функции 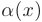на функцию 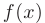, имеющую ненулевой предел, есть бесконечно малая функция:
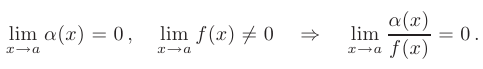
- Если функция 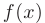имеет предел, равный
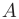, то ее можно представить как сумму числа 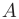и бесконечно малой функции 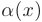и наоборот:
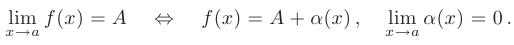
Функция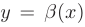 
называется бесконечно большой при 
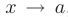, если для любого положительного числа 
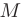найдется такое положительное число 
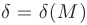, что для всех 
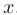, удовлетворяющих неравенству 
, выполняется неравенство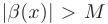 
. В более компактной форме это можно записать так:
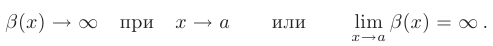
Если бесконечно большая функция принимает только положительные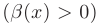 
или только отрицательные значения 
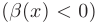, то пишут:
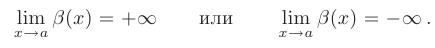
Например, функции
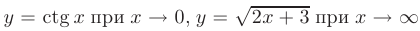
являются бесконечно большими.
Функция 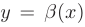, заданная на всей числовой прямой, называется бесконечно большой при 
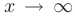если для любого положительного числа 
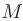найдется такое положительное число 
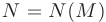, что для всех 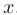, удовлетворяющих неравенству 
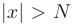, выполняется неравенство 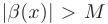. В более компактной форме это можно записать так:
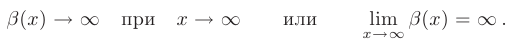
Основные свойства бесконечно больших функций
Пусть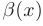 
— бесконечно большая функция: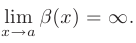 
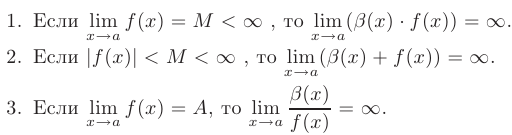
- Функция, обратная к бесконечно малой
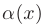, есть бесконечно большая функция и наоборот:
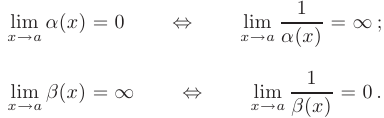
Очевидно, что сумма и произведение бесконечно больших функций есть функция бесконечно большая. Однако разность и частное двух бесконечно больших величин зависит от их характера. Также отношение двух бесконечно малых или бесконечно больших функций может вести себя различным образом в зависимости от их характера. Поэтому такие выражения называют неопределенностями. Выяснение чему в конкретном случае равен предел неопределенности называют раскрытием неопределенности.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Функция одной переменной в математике |
| Предел функции в математике |
| Раскрытие неопределённостей в математике |
| Непрерывность функции в математике |
