Оглавление:
Бесконечно малые и бесконечно большие функции
Определение 3.5. Функция 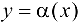 называется бесконечно малой функцией (БМФ) в точке
называется бесконечно малой функцией (БМФ) в точке 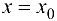 (или при
(или при 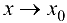 ), если
), если 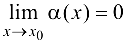 .
.
По определению предела функции в точке:
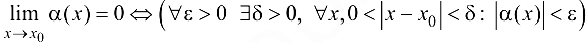
Аналогичным образом определяются бесконечно малые функции (БМФ) при 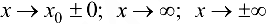 .
.
Теорема 3.3. Алгебраическая сумма и произведение любого конечного числа БМФ при 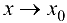 , а также произведение БМФ на ограниченную функцию, являются БМФ при
, а также произведение БМФ на ограниченную функцию, являются БМФ при 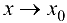 .
.
Доказательство следует из определения предела функции по Гейне и теорем о БМП.
Пусть в некоторой проколотой окрестности точки 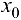 определены функции
определены функции 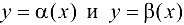 , являющиеся БМФ при
, являющиеся БМФ при 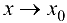 .
.
Определение 3.6. Функция 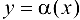 называется БМФ более высокого порядка, чем
называется БМФ более высокого порядка, чем 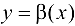 при
при 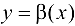 , если
, если 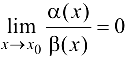 .
.
Если при этом 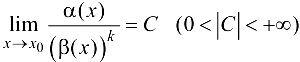 , то
, то 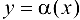 называется БМФ порядка
называется БМФ порядка 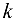 по сравнению с БМФ
по сравнению с БМФ 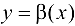 при
при 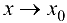 .
.
Обозначается: 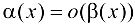 при
при 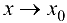 .
.
Определение 3.7. Функции 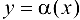 и
и 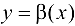 называются БМФ одного порядка при
называются БМФ одного порядка при 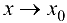 , если
, если 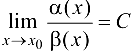 , где С — конечное число, отличное от нуля.
, где С — конечное число, отличное от нуля.
Определение 3.8. Функции 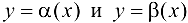 называются эквивалентными БМФ при
называются эквивалентными БМФ при 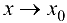 , если
, если 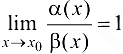 .
.
Обозначается: 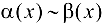 при
при 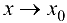 .
.
Пример 3.10.
Функции 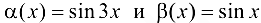 являются при
являются при 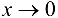 БМФ одного порядка.
БМФ одного порядка.
Действительно,
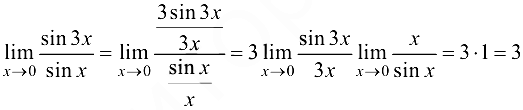
Пример 3.11.
Функция 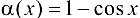 является при
является при 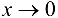 БМФ второго порядка малости по отношению к БМФ
БМФ второго порядка малости по отношению к БМФ 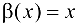 .
.
Действительно,
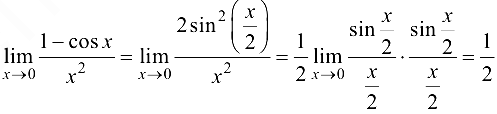
Теорема 3.4*. Предел произведения или частного БМФ не изменится, если любую из них заменить эквивалентной ей БМФ.
Пусть 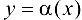 — БМФ при
— БМФ при 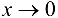 .
.
Имеют место следующие эквивалентности:
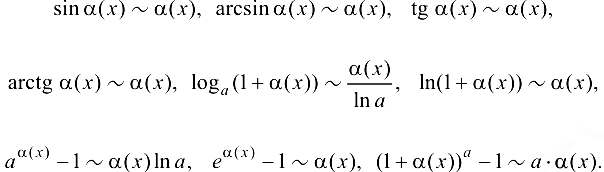
Пример 3.12.
Вычислить 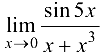 .
.
Решение:
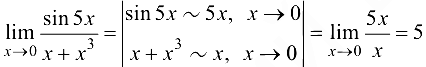
Ответ: 5.
Как и в случае установленной в теореме 2.2 связи последовательности, ее предела и БМП, аналогичная связь наблюдается и между функцией, ее пределом и БМФ.
Теорема 3.5. Число А является пределом функции 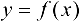 в точке
в точке 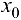 тогда и только тогда, когда имеет место равенство
тогда и только тогда, когда имеет место равенство
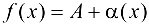
где  — БМФ при
— БМФ при 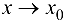 .
.
Доказательство.
Необходимость.
Пусть 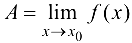 . Тогда, обозначив
. Тогда, обозначив 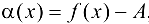 , получим
, получим
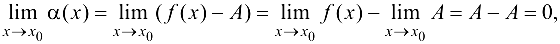
т. е. 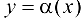 — БМФ при
— БМФ при 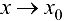 .
.
Достаточность. Пусть 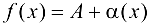 , где
, где 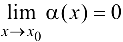 .
.
Покажем, что 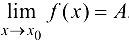 . Имеем
. Имеем
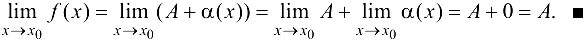
Определение 3.9. Функция 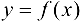 называется бесконечно большой функцией (ББФ) в точке
называется бесконечно большой функцией (ББФ) в точке 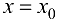 (или при
(или при 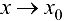 ), если
), если 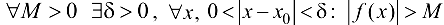 . В этом случае пишут:
. В этом случае пишут: 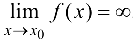 . Если
. Если 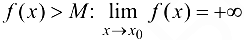 , если
, если 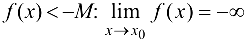 .
.
По аналогии с ББП, можно сформулировать основные свойства ББФ:
1. Произведение двух ББФ есть ББФ.
2. Если в некоторой проколотой окрестности точки 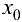 для функции
для функции 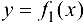 выполнено условие
выполнено условие 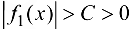 , где С — константа, а
, где С — константа, а 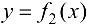 — ББФ при
— ББФ при  , то функция
, то функция 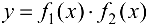 — ББФ при
— ББФ при  .
.
3. Если 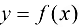 — ББФ при
— ББФ при  , то функция
, то функция 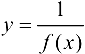 БМФ при
БМФ при  . Если
. Если 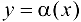 — БМФ при
— БМФ при  (причем
(причем 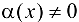 в некоторой проколотой окрестности точки
в некоторой проколотой окрестности точки 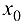 ), то функция
), то функция 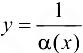 — ББФ при
— ББФ при 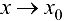 .
.
Заметим, что в случае вычисления предела выражения 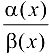 при
при 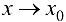 , где
, где 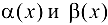 — БМФ при
— БМФ при 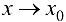 , считают, что получена неопределенность типа
, считают, что получена неопределенность типа 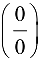 ; в случае вычисления предела выражения
; в случае вычисления предела выражения 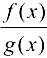 при
при 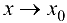 , где
, где 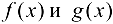 — ББФ при
— ББФ при 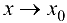 , считают, что получена неопределенность типа
, считают, что получена неопределенность типа 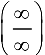 ; в случае вычисления предела выражения
; в случае вычисления предела выражения 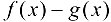 при
при 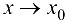 , где
, где  — ББФ при
— ББФ при 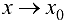 , считают, что получена неопределенность типа
, считают, что получена неопределенность типа 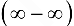 ; в случае вычисления предела выражения
; в случае вычисления предела выражения 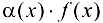 при
при 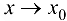 где
где 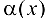 есть БМФ и
есть БМФ и 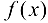 есть ББФ при
есть ББФ при 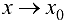 , считают, что получена неопределенность типа
, считают, что получена неопределенность типа 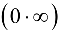 . В решении задач встречаются также неопределенности типа
. В решении задач встречаются также неопределенности типа 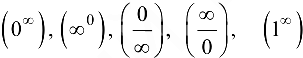 . Выражение «раскрыть неопределенность» означает — найти предел соответствующего выражения, если он существует.
. Выражение «раскрыть неопределенность» означает — найти предел соответствующего выражения, если он существует.
Пример 3.13.
Вычислить 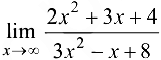 .
.
Решение:
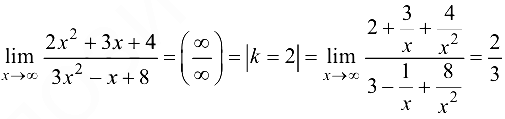
Ответ:  .
.
Пример 3.14.
Вычислить 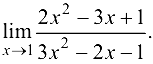 .
.
Решение:
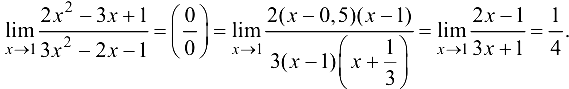
Ответ: 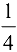 .
.
Пример 3.15.
Вычислить 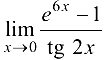 .
.
Решение:
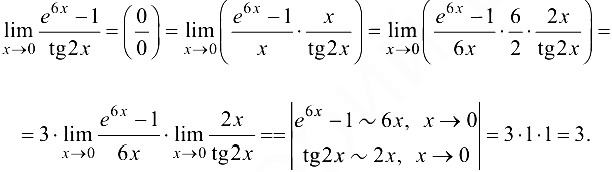
Ответ: 3.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

