Оглавление:
Бесконечно малые функции (б.м.ф.)
Определения и основные теоремы
Функция  называется бесконечно малой при
называется бесконечно малой при  ,
,
если

По определению предела функции равенство (17.1) означает: для любого числа 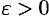 найдется число
найдется число 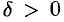 такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 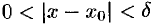 , выполняется неравенство
, выполняется неравенство 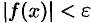 .
.
Аналогично определяется б.м.ф. при 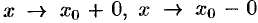 ,
, 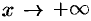 ,
, 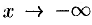 : во всех этих случаях
: во всех этих случаях 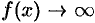 .
.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами 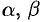 и т. д.
и т. д.
Примерами б.м.ф. служат функции 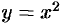 при
при 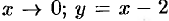 при
при 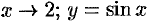 при
при 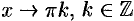 .
.
Другой пример: 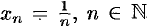 , — бесконечно малая последовательность.
, — бесконечно малая последовательность.
Теорема 17.1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Пусть 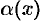 и
и 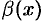 — две б.м. функции при
— две б.м. функции при  . Это значит, что
. Это значит, что 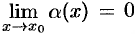 , т. е. для любого
, т. е. для любого 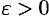 , а значит, и
, а значит, и 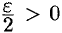 найдется число
найдется число 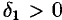 такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 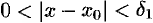 , выполняется неравенство
, выполняется неравенство

и 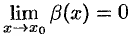 , т. е.
, т. е.
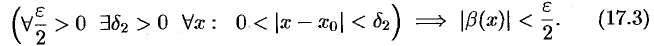
Пусть 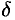 — наименьшее из чисел
— наименьшее из чисел 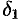 и
и 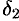 . Тогда для всех
. Тогда для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 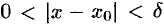 , выполняются оба неравенства (17.2) и (17.3). Следовательно, имеет место соотношение
, выполняются оба неравенства (17.2) и (17.3). Следовательно, имеет место соотношение
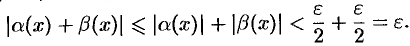
Таким образом,
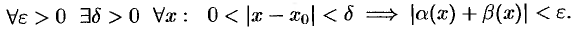
Это значит, что 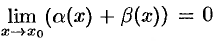 , т. е.
, т. е. 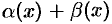 — б.м.ф. при
— б.м.ф. при  .
.
Аналогично проводится доказательство для любого конечного числа б.м. функций.
Теорема 17.2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Пусть функция  ограничена при
ограничена при  . Тогда существует такое число
. Тогда существует такое число 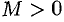 , что
, что

для всех  из
из 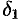 -окрестности точки
-окрестности точки  . И пусть
. И пусть 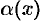 — б.м.ф. при
— б.м.ф. при  . Тогда для любого
. Тогда для любого 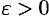 , а значит, и
, а значит, и 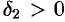 найдется такое число
найдется такое число 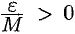 , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 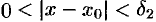 , выполняется неравенство
, выполняется неравенство

Обозначим через 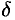 наименьшее из чисел
наименьшее из чисел 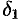 и
и 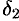 . Тогда для всех
. Тогда для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 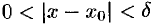 , выполняются оба неравенства (17.4) и (17.5). Следовательно,
, выполняются оба неравенства (17.4) и (17.5). Следовательно, 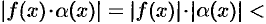
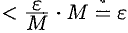 . А это означает, что произведение
. А это означает, что произведение 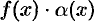 при
при  есть бесконечно малая функция.
есть бесконечно малая функция.
Следствие 17.1. Так как всякая б.м ф. ограничена, то из теоремы (17.2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 17.2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 17.3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Пусть 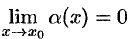 , a
, a 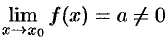 . Функция
. Функция 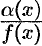 может быть представлена в виде произведения б.м.ф.
может быть представлена в виде произведения б.м.ф. 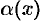 на ограниченную функцию
на ограниченную функцию 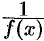 . Но тогда из теоремы (17.2) вытекает, что частное
. Но тогда из теоремы (17.2) вытекает, что частное 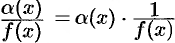 есть функция бесконечно малая.
есть функция бесконечно малая.
Покажем, что функция 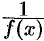 ограниченная. Возьмем
ограниченная. Возьмем 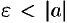 . Тогда, на основании определения предела, найдется
. Тогда, на основании определения предела, найдется 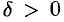 , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 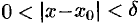 , выполняется неравенство
, выполняется неравенство 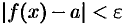 . А так как
. А так как  , то
, то 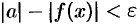 , т. е.
, т. е. 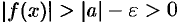 . Следовательно,
. Следовательно,
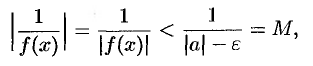
т.е. функция 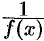 — ограниченная.
— ограниченная.
Теорема 17.4. Если функция 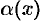 — бесконечно малая
— бесконечно малая 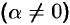 , то функция
, то функция 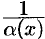 есть бесконечно большая функция и наоборот: если функция
есть бесконечно большая функция и наоборот: если функция  — бесконечно большая, то
— бесконечно большая, то 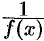 — бесконечно малая.
— бесконечно малая.
Пусть 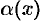 есть б.м.ф. при
есть б.м.ф. при  , т. е.
, т. е. 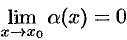 . Тогда
. Тогда
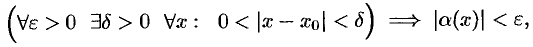
т.е. 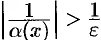 , т.е.
, т.е. 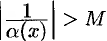 , где
, где 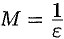 . А это означает, что функция есть бесконечно большая. Аналогично доказывается обратное утверждение.
. А это означает, что функция есть бесконечно большая. Аналогично доказывается обратное утверждение.
Замечание: Доказательства теорем приводились для случая, когда  , но они справедливы и для случая, когда
, но они справедливы и для случая, когда 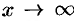 .
.
Пример №17.1.
Показать, что функция
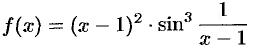
при 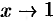 является бесконечно малой.
является бесконечно малой.
Решение:
Так как 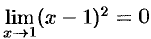 , то функция
, то функция 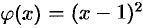 есть бесконечно малая при
есть бесконечно малая при 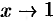 . Функция
. Функция 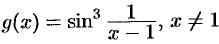 , ограничена
, ограничена 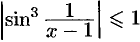 .
.
Функция 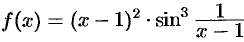 представляет собой произведение ограниченной функции
представляет собой произведение ограниченной функции 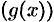 на бесконечно малую
на бесконечно малую 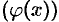 . Значит,
. Значит,  — бесконечно малая при
— бесконечно малая при 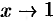 .
.
Связь между функцией, ее пределом и бесконечно малой функцией
Теорема 17.5. Если функция  имеем предел, равный
имеем предел, равный  , то ее можно представить как сумму числа
, то ее можно представить как сумму числа  и бесконечно малой функции
и бесконечно малой функции 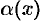 , т. е. если
, т. е. если 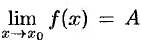 , то
, то 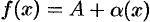 .
.
Пусть 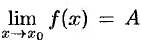 . Следовательно,
. Следовательно,
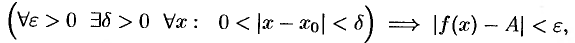
т. е. 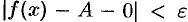 . Это означает, что функция
. Это означает, что функция 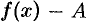 имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через
имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через 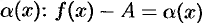 . Отсюда
. Отсюда 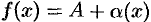 .
.
Теорема 17.6 (обратная). Если функцию  можно представить в виде суммы числа
можно представить в виде суммы числа  и бесконечно малой функции
и бесконечно малой функции 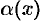 , то число
, то число  является пределом функции
является пределом функции  , т. е. если
, т. е. если 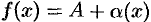 , то
, то 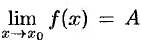 .
.
Пусть 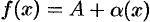 , где
, где 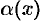 —б.м.ф. при
—б.м.ф. при  , т. е.
, т. е. 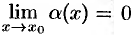 . Тогда
. Тогда
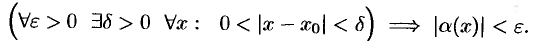
А так как по условию 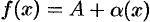 , то
, то 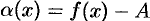 . Получаем
. Получаем
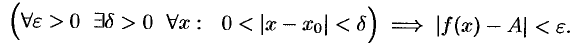
А это и означает, что 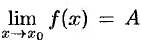 .
.
Пример №17.2.
Доказать, что 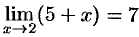 .
.
Решение:
Функцию 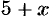 можно представить в виде суммы числа 7 и б.м.ф.
можно представить в виде суммы числа 7 и б.м.ф. 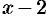 (при
(при 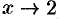 ), т. е. выполнено равенство
), т. е. выполнено равенство 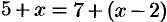 . Следовательно, по теореме 17.6 получаем
. Следовательно, по теореме 17.6 получаем 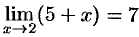 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Предел функции при х к бесконечности |
| Бесконечно большая функция |
| Основные теоремы о пределах |
| Признаки существования пределов |

