Оглавление:
Бесконечно большие и бесконечно малые последовательности
Определение 2.6. Последовательность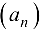 
называется бесконечно большой последовательностью (ББП), если для 
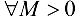(сколь бы большим его ни взяли) 
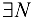такой номер, что для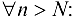 
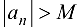
Заметим, что если последовательность бесконечно большая, то опа является неограниченной, но не наоборот, т. е. неограниченная последовательность не обязательно будет ББП.
Определение 2.7. Последовательность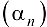 
называется бесконечно малой последовательностью (БМП), если для 
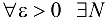такой номер, что для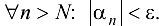 
Пример 2.4.
.
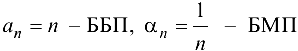Теорема 2.1. Если последовательность 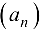— ББП. и все ее члены отличны от нуля 
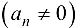, то последовательность 
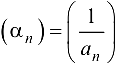будет БМП; и обратно, если 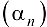— БМП. 
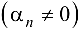то последовательность 
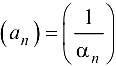— ББП.
Доказательство.
Пусть 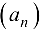— ББП. Рассмотрим 
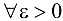и положим 
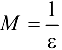. Согласно определению ББП, для этого М будет 
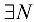такой помер, что для 
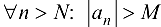. Тогда
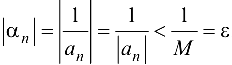
т. е. для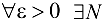 
, что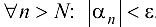 
. А это и означает, что
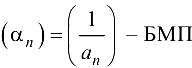
Аналогично доказывается вторая часть теоремы. ■
Свойства БМП
- Алгебраическая сумма любого конечного числа БМП есть БМП.
- Произведение любого конечного числа БМП есть БМП.
- Произведение ограниченной последовательности на БМП есть БМП.
Следствие 2.1*. Произведение БМП па число есть БМП.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
