Бесконечно большая функция (б.б.ф.)
Функция  называется бесконечно большой при
называется бесконечно большой при  , если для любого числа
, если для любого числа 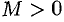 существует число
существует число 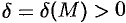 , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 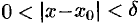 , выполняется неравенство
, выполняется неравенство 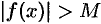 . Записывают
. Записывают 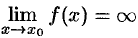 или
или 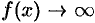 при
при 
Коротко:
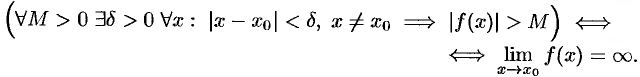
Например, функция 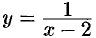 есть б.б.ф. при
есть б.б.ф. при 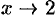 .
.
Если  стремится к бесконечности при
стремится к бесконечности при  и принимает лишь положительные значения, то пишут
и принимает лишь положительные значения, то пишут 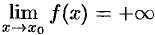 ; если лишь отрицательные значения, то
; если лишь отрицательные значения, то 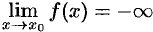 .
.
Функция  , заданная на всей числовой прямой, называется бесконечно большой при
, заданная на всей числовой прямой, называется бесконечно большой при 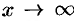 , если для любого числа
, если для любого числа 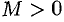 найдется такое число
найдется такое число 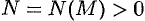 , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 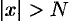 , выполняется неравенство
, выполняется неравенство 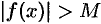 . Коротко:
. Коротко:
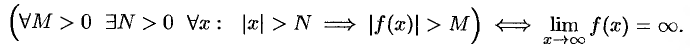
Например, 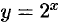 есть б.б.ф. при
есть б.б.ф. при 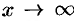 .
.
Отметим, что если аргумент  , стремясь к бесконечности, принимает лишь натуральные значения, т. е.
, стремясь к бесконечности, принимает лишь натуральные значения, т. е. 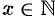 , то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность
, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность 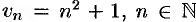 , является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки
, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки  является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например,
является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, 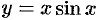 .)
.)
Однако, если 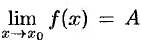 , где
, где  — конечное число, то функция
— конечное число, то функция  ограничена в окрестности точки
ограничена в окрестности точки  .
.
Действительно, из определения предела функции следует, что при  выполняется условие
выполняется условие 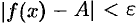 . Следовательно,
. Следовательно, 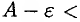
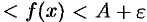 при
при 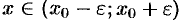 , а это и означает, что функция
, а это и означает, что функция  ограничена.
ограничена.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Односторонние пределы |
| Предел функции при х к бесконечности |
| Бесконечно малые функции |
| Основные теоремы о пределах |

