«Берущиеся» и «Неберущиеся» интегралы
Как уже отмечалось выше, операция интегрирования функций значительно сложнее операции дифференцирования функций. Не всегда выбранный путь интегрирования является наилучшим, более коротким, простым. Интегрирование часто может быть выполнено не единственным способом. Многое зависит от знания рекомендуемых многих искусственных приемов интегрирования, от сообразительности, от тренированности. Например, 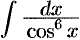 можно найти, не используя рекомендуемую подстановку
можно найти, не используя рекомендуемую подстановку 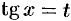 , а применив искусственный прием:
, а применив искусственный прием:
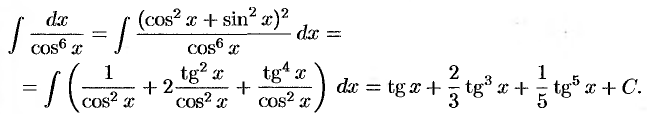
Вряд ли стоит вычислять интеграл
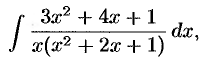
разлагая подынтегральную функцию на простейшие дроби:
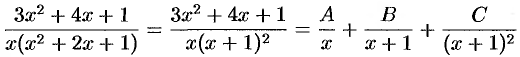
Заметив, что числитель 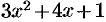 является производной знаменателя
является производной знаменателя 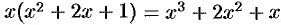 , легко получить:
, легко получить:
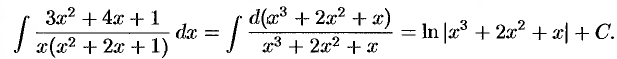
На практике при вычислении неопределенных интегралов используют различные справочники, содержащие таблицы особенно часто встречающихся интегралов. В частности, «Таблицы неопределенных интегралов» М. Л. Смолянского.
Изученные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл, т. е. найти первообразную функцию для подынтегральной функции.
Как известно, всякая непрерывная функция имеет первообразную. В том случае, когда первообразная некоторой элементарной функции  является также элементарной функцией, говорят, что
является также элементарной функцией, говорят, что 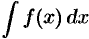 «берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» (или «его найти нельзя»).
«берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» (или «его найти нельзя»).
Так, например, нельзя взять интеграл 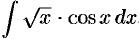 , так как не
, так как не
существует элементарной функции, производная от которой была бы равна 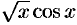 . Приведем еще примеры «неберущихся» интегралов, которые имеют большое: значение в приложениях:
. Приведем еще примеры «неберущихся» интегралов, которые имеют большое: значение в приложениях:
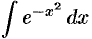 — интеграл Пуассона (теория вероятностей),
— интеграл Пуассона (теория вероятностей),
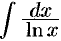 — интегральный логарифм (теория чисел),
— интегральный логарифм (теория чисел),
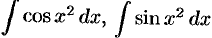 — интегралы Френеля (физика),
— интегралы Френеля (физика),
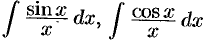 — интегральные синус и косинус,
— интегральные синус и косинус,
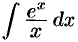 — интегральная показательная функция.
— интегральная показательная функция.
Первообразные от функции 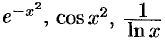 и других хорошо изучены, для них составлены подробные таблицы значений для различных значений аргумента
и других хорошо изучены, для них составлены подробные таблицы значений для различных значений аргумента  .
.



На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегралы типа r x (ax^2+bx+c) dx |
| Интегрирование дифференциального бинома |
| Определенный интеграл как предел интегральной суммы |
| Геометрический и физический смысл определенного интеграла |

