Балка, заделанная одним концом и опертая другим

Оглавление:

Балка, заделанная одним концом и опертая другим

Загерметизируйте одну сторону с Лучом и поддержите другую сторону В этом случае имеется 3 неизвестных реакционных элемента на одном конце и 1 неизвестный реакционный элемент на другом конце. Поэтому задачи не могут быть определены статически в прошлом.

Начните с 1 сосредоточенной нагрузки (P) (рис.157, А) и рассмотрите ненужное крепление, которое предотвращает вращение левого конца a балки psi во время изгиба. Отказ от этого исправления приведет к статически определяемой проблеме, как показано на рисунке. 157, B. изгиб, вызванный статически неопределенной парой MD, разбивается индивидуально, как показано на рисунке 5. 157, С1).

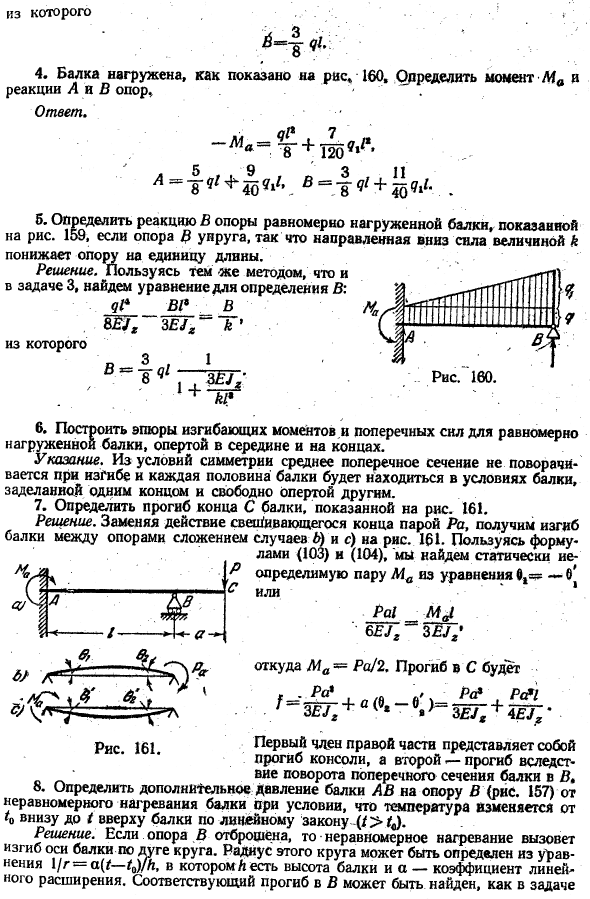
Очевидно, что изгиб балки 157, показанный на рисунке, а может быть получен путем сложения случая (Б) и (в). Необходимо выбирать значение пары Ма на опоре только в том случае, если условие (ля） Рисунок 157. Таким образом, самый левый поворот пучка от силы P разрушается условиями пустотного момента Ma и вложенного con. п * к&CE, то есть, угол наклона здесь Вена к zero.

To получим статически неопределенную пару Ма, просто вставив известные значения углов (88) и (104) 61 и 6 в уравнение (а).И затем… / > <. (/- с*) МА1 SH7T-ВВ Откуда? ПК(P-s *） (107） В. График изгибающего момента можно получить путем сложения фигур в фигурах (b) и ©. 157 D максимальный изгибающий момент, А или в(I.•、

Из отклонения в этом отношении, вызванного сосредоточенной нагрузкой P (рис.157, 6), отклонение в любой точке может быть легко получено путем вычитания отклонения, вызванного парой Ma (рис. 157, c).Уравнение криволинейной оси для обоих этих случаев приведено уже в (86) И (87) стр. 129 и (105), стр. 141. Людмила Фирмаль

Например<,/ x) диаграмма оси кривой и изгибающего момента белка отображается вместе. Рассчитайте отклонение f в центре пролета. Из формул (91)и (105)、 л-мсрч-Ж + М;- Или используя формулу (107)、 — ШГ& ’ — БЖ- В точке С, где изгибающий момент равен нулю, кривизна изгибающей оси балки также равна нулю, и мы тоже.

Существует точка перегиба, то есть точка, в которой изменяется знак кривизны. Из Формулы (107)видно, что изгибающий момент на замкнутом конце зависит от расположения нагрузки P. когда производная формулы (107) относительно c равна нулю, момент Ma равен c = / / / ^ h. после этого Аум. х = 3Вт =° ’I92P /- (108）

Изгибающий момент при нагрузке, 157 от фиг, d равен МД =£^>-я -^= Г(я-с) ’(2 / + с). (си） возьмем производную (b) по отношению к c и пусть она равна нулю, тогда Ма равна С = ^ (] / 3-0 = 0.366 Я Если мы присвоим его формуле (b)、 (Аун Старый. х = 0.174 П /. Если сравнить это с формулой (108), то в случае движущихся нагрузок максимальное вертикальное напряжение находится в замкнутой части и、 / с

Существует решение для 1 концентрированной нагрузки, используя метод сложения силового воздействия 158、 Используя приведенную выше теорию, решается задача о других видах поперечных нагрузок. Например, рассмотрим случай, показанный на рисунке. 158.

Момент на опоре а, возникающий в результате основной нагрузки qdc, получается из Формулы (107)путем подстановки qdc вместо P. Ma поддержите полный момент ’ Если нагрузка распределяется по всей длине балки (рис. 159, а), подставляя a = 0, b-/в Формулу ©, то、 * М. —%. (109)） Так… Тттптнжт а) фигура изгибающего момента получается путем вычерчивания треугольной фигуры из пары Ма (рисунок 159) из параболической диаграммы равномерной нагрузки.

Отклонение в любой точке Рисунок 159.Луч получается путем вычитания отклонения Эта точка из пары Ма (уравнение(105)) является точкой отклонения в той же точке от равномерной нагрузки (уравнение (81)).Далее, примерно в середине пролета Л. Зи. Д / Ф. =(110） 1 заказ] g 16 192 EJJ ^ k ’ Задачи 1.157 и 159 для построения графика силы сдвига в случае, показанном на фиг. 2.

Максимальное нормальное напряжение на изгиб В раздел. Людмила Фирмаль

Определите максимальное отклонение, когда нагрузка, показанная на рисунке, равномерно распределена. 159. Решение. Если сложить формулы (81) и (105), то получим следующую формулу для криволинейной оси: Г=（3 / ^ −5 / ** + 2х ). (<3） Если вы установите производную yy / yx в ноль, x==（// 16）（15 —V33) = 0,579 / находит максимальное отклонение. когда (b) заменяется、 /—?** 。 ’gaah \ bbEJg 3.

Определите противодействие опоры правой балки, показанное на рисунке. 159, считайте эту реакцию ненужной неизвестной. Решение. Если опору B отбросить, то из Формулы (84) отклонение этого конца балки, который считается консольным, будет равно dP. Седзи.

Реакция B должна быть такой, что она разрушит указанное отклонение. Затем, используя уравнение (95), получаем уравнение. ДОКТОР ВР. что это?*• Оттуда 4.Нагрузка приложена к лучу как показано в диаграмме * 160.Реакция опор определяет моменты моментов а и В.* Ответ. «м» 〜ДТ + тя СТ4 ** + 2е^. 。 8. 40. a. реакция определяется равномерно нагруженной опорой балки, как показано на Рис.1. 159, если опора B эластична, то нисходящая сила величины k понижает опору в единицах длины.

Решение. Используйте тот же метод, что и в задаче 3, чтобы найти уравнение, определяющее B. 7. 。 ДОКТОР ВР. Б. 。 Ю; 3£/ * » к *.• Оттуда 1. Б — = / сек / 6.Создайте график изгибающего момента и силы сдвига равномерно нагруженных балок, поддерживаемых в центре и по краям. Из условия знака-симметрии, средняя площадь поперечного сечения не вращается даже при изгибе, и каждая половина балки находится в состоянии балки, один конец которой герметизирован, а другой свободно поддерживается. 7.

Определите отклонение конца с балки, которое показано на рисунке. 161. Решение. Если заменить операцию подвешивания торца парой ПА, то, добавив корпус Б) и в) На рисунке б, вы получите изгиб балки между опорами. 161.Используя уравнения (103) и (104), найдите пары Ma, которые могут быть определены с помощью UE-P статически из уравнения. Инжир. 161. 。 Ра. \ MJ 3 EJZ ’ 6EJZ Оттуда Ma = Ra / 2. Прогиб с д. РА ’ ^ Л / А: Ра *. RL / 3EJt * * 3EJ、*

Первый элемент справа-это прогиб консоли, а второй-прогиб за счет поворота балки поперечного сечения В. 8.Если температура изменяется от t0 до t в верхней части балки по линейному закону, определить давление балки АВ на опоре Б (рис. 157) от неравномерного нагрева пучка.

Решение. Когда опора B отбрасывается, когда нагрев становится неравномерным, ось балки изгибается вдоль дуги. Радиус этой окружности можно определить из уравнения L / Р = А (Ф-tjfh. Где A-высота балки, а a-коэффициент линейного расширения. Соответствующее отклонение B можно найти как в задаче, / * / * a (<- /p） 1, 27, 2л. Эта проблема должна быть уничтожена ответом поддержки L. 5 означает эту реакцию.

Тогда мы получаем В1д о） Откуда? 9.Консоль LP (рис.162), загруженная на конце B, находится на короткой консоли с тем же поперечным сечением, что и консоль AB. Определить давление х между 2 балками в точке С. 。Решение. Давление X определяется из условия, что обе консоли имеют одинаковый прогиб в точке C. используйте формулу (95)для нижней консоли и Формулу (95) для верхней консоли вместе с Формулой (97), чтобы получить следующее:

Откуда? Рассматривая диаграмму изгибающего момента верхнего и нижнего кантилевера, можно сделать вывод, что в точке с Верхний кантилевер имеет больший угол наклона, чем нижний. Это указывает на то, что соединение между 2 консолями находится только в точке C и I. 10.Вместо сосредоточенных нагрузок решают задачу 7, предполагая, что равномерная нагрузка прочности q распределяется по длине подвешенного конца, а 2) по всей длине балки.

Строит графики изгибающих моментов этих 2 случаев и сдвиговых сил. 11.158 для построения графика изгибающего момента и силы сдвига, когда показано на рисунке, a равно 1. 2 м, если b равно 3,6 м, то I = 4. 5 лир 500 кг / м.

Балка с двумя заделанными концами	Влияние поперечных сил на прогиб балок
Рамы	Лишние закрепления