




- Такая же методика применяется и к турбулентному пограничному слою на плоской поверхности. Было бы желательно применить логарифмическое распределение скорости к потоку пограничного слоя. Формула (13. 58)-(13. 60). Вы можете сделать это, но используйте более простую формулу для распределения скорости, потому что вывод и конечная связь сложны и громоздки. Для течения в трубе до He = 105 уравнение является подходящим.
Это уравнение можно также назвать законом корня 7-го порядка (закон брасиуса).Запишите это соотношение пограничного слоя на пластине в следующем формате Формула (13. 96) (13. При подстановке (86) получается последующий Интеграл. = 72 7 б * (13.97) Формула (13. 84) эффективен для слоев жидкости, прилегающих к стенкам, даже в пределах турбулентных пограничных слоев. Однако формула(13. 96) отключается, когда y стремится к нулю.
Поэтому для определения напряжения стенки используют формулу брасиуса о коэффициенте сопротивления при движении по трубе. Эта формула-формула(13. 71) — 7 соответствует распределению скорости по следующему корневому закону / = 0,079 Из Формулы (13.67)、 = Т =(13-98) Это уравнение для трубы можно применить к течению пограничного слоя на пластине, заменив O = 26 и u = 0.817 Ish = 0.817 u0.Результат、 = 0.023 в1 / 4. (£13.99)) Уравнение (13. 99) и (13. 97), и представляют их в целостной форме = 0,023 О, да.
И так оно и есть. (13.101) д-0,376 Или б = 0.376be2 ’/ аль. (13.102) интегрирование силы сопротивления от x-0 до X-b происходит в нескольких случаях (Формула (12. 78)и ниже), как это было сделано ранее、 Co = 0.072 Будет ’ 1 /’. (13.103) В сделанном выводе считалось, что турбулентный пограничный слой простирается от x = 0, но на практике на некоторых участках фронта пластины пограничный слой является Рами Палленом. Сравнивая результаты ламинарного пограничного слоя с турбулентным пограничным слоем, можно видеть, что BH \в случае ламинарного движения и B увеличивается в случае турбулентного течения. Ra увеличивается как L *в ламинарном потоке, так и X * / в турбулентном потоке.
Это количественные причины, которые пытаются сохранить ламинарный пограничный слой крыла, как объяснено в первой части этой главы. Аналогично, формула(13. 102) и (13. 103) применение ограничено рядом 5-105-107.It это точно такой же метод, как и в случае с потоком трубы. Если на выходе используется логарифмическое распределение скорости, то вы получите результаты, подходящие для очень высоких значений .
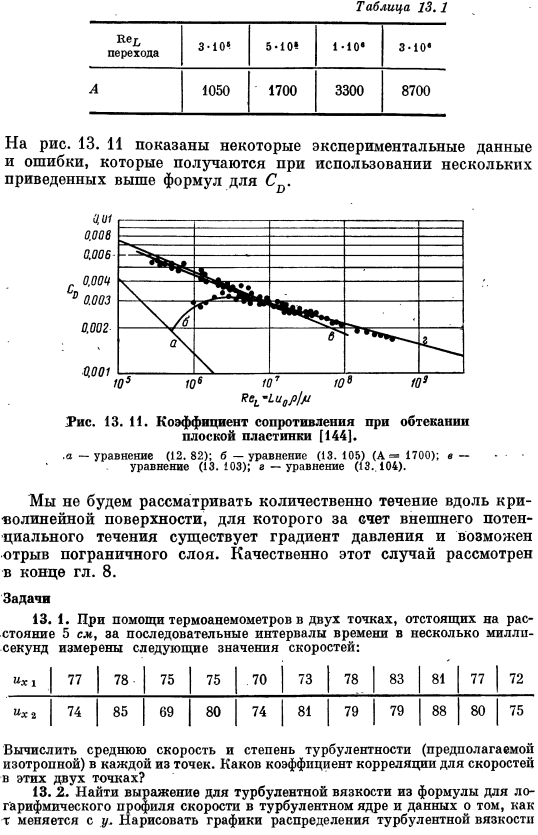
Для плоской пластины, результат такого расчета может быть выражен следующей формулой 0.455 (18 Nei) 2″ 58″ (13.104) Если преобразовать это соотношение с учетом наличия слоистого слоя перед частью пластины, то получится формула плантра шлитчинга. где а-функция критического числа Рейнольдса Be^^, определяемая степенью турбулентности внешнего потока, а величина а приведена в таблице. 13.1. Таблица 13.1 Переход ke 310 * 5-10 * 1-10e 3-10 * 1050 1700 3300 8700 13.Некоторые экспериментальные данные и несколько ИСВ. 13. I. коэффициент сопротивления при обтекании плоской пластины [144] а-уравнение 12.
- Он не учитывает количественно течение вдоль криволинейной поверхности, где существует градиент давления, обусловленный внешним потенциальным потоком и отрывом пограничного слоя. possible. In качественными терминами этот случай называется ч. 8. Задачи 13. 1.At непрерывный интервал времени в несколько миллисекунд, используя термоанемометр в 5 точках с интервалом в 2 сантиметра, измеряли следующие скорости: XI 77 78 75 75 70 70 73 78 83 81 77 72 «Ха» 74 85 69 80 74 81 79 79 88 80 75 Вычислите среднюю скорость и степень турбулентности (предполагается, что она изотропна) в каждой точке.
Каков коэффициент корреляции скорости в этих 2 точках? 13. 2.Найти уравнение логарифмического профиля скорости турбулентного ядра и уравнение турбулентной вязкости и данные о том, как изменяется m с y. построить график распределения турбулентной вязкости по сечению трубы при постоянном He и зависимости xe от конкретной точки На Be. Ли сумма зависеть будет? С позиции? 15. 3.Действуйте так же, как и в предыдущей задаче, и найдите распределение безразмерного смешанного пути.
Показывает, как эта сумма зависит от Be и позиции. 13. 4.Формула (13. 58)〜(13. 60), что не соответствует профилю скорости, полученному из простых физических соображений. При решении задачи учитывайте значение 13. 5. Вода при температуре 20°с движется по гладкой горизонтальной трубе диаметром 50 мм вгнг-п-П1шм. Для точек на расстоянии 18 мм от стенки рассчитайте траекторию смешения со скоростью, напряжением сдвига, турбулентной вязкостью и средней скоростью потока.
Да, он движется таким же образом. Выпуск 13. То же самое, что и 5, но с грубой отделкой. Вычислите те же 4 величины для тех же точек в А)B = 15 м / С, Е / Н = 0.01; б) u-1,5 м / с, e / g \ = 0,03; c) b 1,5 м / с, e / c = 0,0005; г) Б-0,015 м / с, е / Г1-0,01. НЯ ^ вглиа в трубке? Для сопротивления в потоке распределение скоростей по корневому законуblблазиуса 7 градусов-1 / м. уравнение (1°.ЕЭС). используя уравнение баланса импульса l «D3», мы выводим формулу для b, исходя из предположения, что скорость пограничного слоя на гладкой плоской пластине изменяет толщину HTI, и формулу.
При протекании воды вокруг пластины на расстоянии пограничного слоя^ 0.3 со скоростью 20°С в Умл м **** 1вму от передней кромки определяется суммарное сопротивление участка до точки вопроса шириной 1 м? ««9» воздух при атмосферном давлении и 20 ° С течет плавно Сляб со скоростью 30 м / с. Как далеко находится точка перехода ламинарного пограничного слоя к турбулентности от передней кромки? «аСЛИ_Т? Р? Ж1е? Переход ke-5-10 *основной поток такой, что он возникает в ГН0Ь. Мы также вычисляем толщину пограничного слоя по расстоянию ?Общее сопротивление участка до этой точки составляет 9 м 0т°Эредиа КРОМКП и 1 м на ширину.
Можно предположить, что пограничный слой, образованный на входе n 10 ’OttP ^ U’, образуется таким же образом, как и пограничный слой на плоской пластине, чтобы уменьшить длину, необходимую для достижения полностью развитого потока.
Смотрите также:
