






- Уравнение баланса импульса (momentum) основано на втором законе Ньютона g 1 (Майк) икс (5.1). Кроме того, задача по своей природе сложнее, чем раньше объясните массу и энергию, достаточно указать их значения. Для силы и импульса также необходимо указать направление, так как эти величины являются векторами. (Рассмотрим только компоненты x этих векторов.) Контролируемый объем определяется таким же образом, как и вывод уравнений материального и энергетического баланса. Сила, действующая на этот объем, определяется скоростью изменения импульса жидкости, проходящей через контролируемый объем в момент движения объекта.
Далее эта величина складывается из суммарного потока импульса через всю управляющую поверхность и скорости изменения суммарного количества импульса в управляющем объеме(напомним, что управляющий объем является стационарным). (5.2)) В этом уравнении, например, DA-это поток жидкости через участок (1A (м3 / с)), а значения rih можно рассматривать как плотность x-компонента импульса (momentum) (kg-m / s) 1m.
Сила Gx создает результирующий Gxr, направленный на противоположную сторону оси x, поскольку давление увеличивается в положительном направлении оси X. Секс; технологию wcn » ЦЖР «GuBdСи ^ ТХ ^ 0Л’», » онлайн Х Тело (пример нано, стенка трубы) n может быть твердым в частях, действующих на внешние силы. * ’Пример-если ранг Kx имеет полностью определенную P3 «Ятваемую трубу», слейте ее. Здесь мы перепишем уравнение A и M°LN° «изменение объемной подынтегральной функции/ n-2 этих сил и величины движения (обозначенной rez)» BB0. Res * * «массовый» вывод- // е » Хи soveil = Формула (5. 3) при применении к сегменту m он ориентирован вдоль оси x, как показано на рисунке.
3. П2, Эл= -, потому что а =±1,0, поэтому (5.3) * «Х3?Матчи УУТРУБЫ ’005К0Т0Р0Р ° лллл ° лллл°». Здесь. (5.4) («X) yer Uy’L. а в случае стационарного уравнения (5. 4) быть、 1-я(Фер = д г _ п х г * ху) » «a08 ggV» ^ xh:^ m; wnp: p / = » и a2 скорость не изменяется、 (5.5)) (5.6)в уравнении состояния текучей среды она становится силой. Уравнение площади (5. 4) если он становится+(5.7) «»Си.«для n, кривой оси должны быть использованы, и импульс должен быть использован.
Уравнение баланса для компонента y (5.8).) Пример(5. 3) в вопросе рассматривается труба с изогнутой осью. Конечно, в более общих случаях следует также рассмотреть уравнение баланса компонента R с числом точек на дюйм> Если труба не горизонтальна, то соответствующая составляющая силы тяжести должна быть включена в правую часть формулы баланса количества. При изучении и проектировании роторной машины действия, такой как турбина или роторный „насос“, уравнение равновесия импульса через крутящий момент и момент k0 „„CESa ““ K0 Такие проблемы не учитываются в других книгах, например Хунзакер и Райтмаир [69]П?
ИВОД1 х помогает решать уравнения пограничного слоя и уравнения движения, когда они учитываются позже, наряду с прямым применением уравнений равновесия импульса, которые показаны в задаче. Вода при расходе 568 л / мин проходит через горизонтальное сопло, точнее, перепад давления dr. Do вы делаете это, когда пирог Пирог? (4. 21), игнорируя трение. Шляпы-Ар д 2 е (1) В зависимости от условий, скорость сечения сопла не изменяется на новый расход. УР = −56 ^ — = 9.47 кг / с За задание Рассчитайте скорость: IV 9.47-4-10 * _o. o7 м / с: «В1 = ^ 7Т〜1000-3.14-7.62」 hb = 2,07-(3/1) = 18,6 м / с.
Из формулы (1) д-р.= _ 08.6) »-(2.07)。 1000 = _1171.10, Ф / w2_175kg / см、 Для определения BX используйте формулу баланса импульса (5. 6) Использование. Аих + Рхр-ВХ. (2) Для решения этой задачи в уравнении баланса импульса сопло 11 °volvolume должно содержать стенку= L! Сила, направленная на фигуру. 5.1 Влрав? И упражнения А2-левая сила p2A2.In кроме того, » асферическое давление во внешней части сопласоздает результирующее давление^равное левому направлению в 1 направлении. Поэтому синтетическая сила giaдиаметр МШ1ЫШШ (рис.6), механическая энергия прпнп? Сходятся к образованию вихря. Постепенно меняется р * р-PaA2 4-па (ЛК-Л2) — PxLx = а, (ПВ-ПВ). Теперь подставим номер выражения (2).
Д8 = 157-777 = −620 Н = −63.4 кг. »*0 ° с Лку Резульпрую1чая сила НХ, приложенная к соплу, отрицательная топишая ось Яо » ₽ » авлгпакс и ток противоположный. Приманка закреплена на входе, поэтому ее стенки растянуты. Пример 5.2 — Лу? А * внезапно расширяется, когда жидкость выходит из жидкости»?Эль’g.1?Л?1diamZR (рисунок 5-2), такие как сопло примера 5, механическая энергия поперечного сечения 1, потери энергии очень малы.
- Используя уравнение баланса импульса, вы получаете уравнение энергии a, потерянной при внезапном расширении потока несжимаемой жидкости. Рассмотрим простой пример, когда скорость обеих труб постоянна в поперечном сечении. Уравнение.>*((О) это、 I7 с ВХ. C6 = — / ’ объявление. Рисунок 5. 2.Расширение потока. * ! — ! ’ ** 1-1 1 0 −2 −2.» * (1) I «» TR°L, wi c6161 *’, окруженный плоскостями 1 и 2, с колпачком, выбранным таким образом, что YX исчезает. Далее, по предположению, она течет только по поверхности PLA0.Все потери вызваны только конверсией, Px&= 0.Вместо этого используйте Pxp L2 (p2 — px). I7Di6 = — П2(Р2-Р1).
Потому что P1 и Rch постоянны по всему сечению трубы、 Это Предусмотренный Po = P1-используя соотношения h = b0 eA и u6r=, уравнение сводится к следующему виду: / ^ » /является уравнением равновесия механической энергии, примененным к этой задаче、 4CH1-Ш- 1 = 2г- Последние 2 уравнения, желаемый результат будет получен Часто, p ^^ PeE (5°)°^^^потеря потеря — ■- Горизонтально расположенные гладкие Как показано^ D ^.^ О » Рассчитаем величину и направление силы, необходимой для удержания колена(в контрольный объем следует включить стенку трубы.
в этой задаче будем считать, что скорость распределяется равномерно, сначала по оси x, а затем в первом направлении * сечения находим следующее: Ту(ix2-Hx1)= — При — (о Потому что точка 2 не имеет скорости^^ c ^ aw*, а * «- выходит » — равно всем направлениям. Таким образом, общая прочность при = — а(ру-Рау, Ях = — топор(Р1-Ра) -= = 3,14-5,1 «(_14).9> 8_a4L0002l (м) −10±а = 4 = —280—1190-=-1470 n = 150 кг. Полная потеря и———• Pa внезапное расширение, более точное представление^ 1 Пример 5. 3. В 90-х годах вода текла из 1 рта、 Как показано на рисунке К / Рисунок 5. 3.Текущий Труба. Изогнутый (4 )) (5) Вход 1.4 at.
Не обращайте внимания на трение Сиппявление Си- Точно так же、 ПУ = П2 (Р2-РО)+ = 280 + 1190 = 1470 Н = 150 кг Результирующая сила равна p = 45°, ее величина равна Меня проинструктировали. 150 / pop 45° = Обозначено 212 кг. Рисунок 5. 3, косые задачи 5. 1.Вода течет через горизонтальный диффузор, который состоит из секции труб, внутренний диаметр которых постепенно увеличивается от 5 см до 10 см. Если расход составляет 3800 л, рассчитайте результирующую силу, действующую на диффузор! Избыточное давление на выходе минимальное и составляет 4,2 атм. 5. 2. Расход воды, протекающей по горизонтально изогнутой части под углом 50°от 45-литровой трубы, эквивалентен 760л!
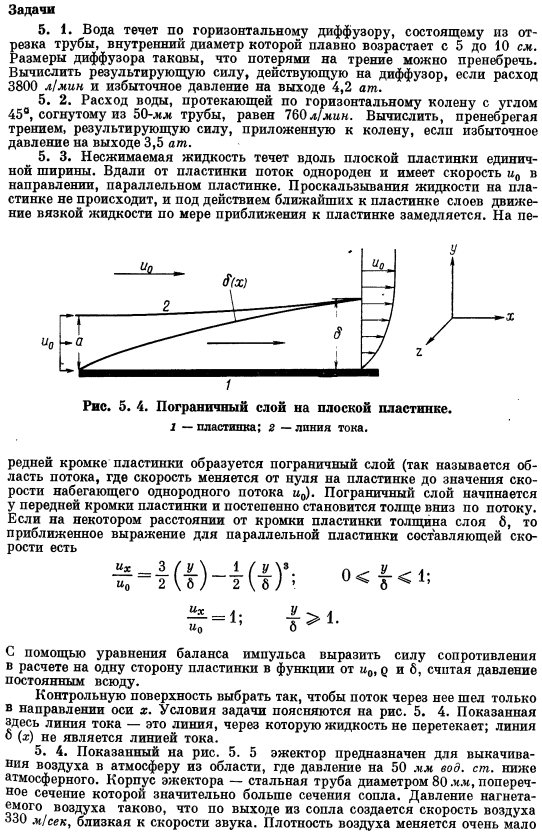
Если избыточное давление на выходе составляет 3,5 Ат, вычислите силу, приложенную к колену, и проигнорируйте трение. 5. 3.Несжимаемая жидкость течет вдоль плоской пластины с единичной шириной. Удаляясь от пластины, поток является равномерным и имеет скорость u0 в направлении, параллельном пластине. Жидкость не скользит по пластине, и под действием слоя, ближайшего к пластине, движение вязкой жидкости замедляется по мере приближения к пластине. plate. To Рисунок 5.
Пограничный слой на плоской пластине. В икс 1-пластина; 2-линия потока. Образуется пограничный слой (так называемая область течения, где скорость изменяется от нуля на пластине до скорости падающего однородного потока и^.Пограничный слой начинается на переднем конце пластины и постепенно утолщается вниз по течению. Немного в стороне от края пластины, для толщины слоя b, приближенная формула параллельной пластины компонента скорости равна Используя уравнение равновесия импульса, мы представляем вычисленные силы сопротивления на одной стороне пластины как функцию u0, p и b, предполагая, что давление везде постоянно.
Выберите управляющую поверхность таким образом, чтобы поток через управляющую поверхность протекал только в направлении оси X. Условие задачи проиллюстрировано на схеме. 5. 4.Линия обтекания, показанная здесь, является линией, в которой жидкость не течет. Линия o (x)не является линией потока. 5. 4.Рисунок 5. 5 эжектор предназначен для закачки воздуха в атмосферу из зоны, где давление воды составляет 50 мм. Искусство. Ниже атмосферы. Тело выталкивателя 80 в диаметре. ч.
К стальной трубы, ее сечение значительно больше, чем сечение сопла. Давление нагнетаемого воздуха таково, что на выходе из сопла создается скорость воздуха АОО м / с, близкая к скорости звука. Плотность воздуха практически не изменяется и может быть принята постоянной на уровне 1,2 кг! Кубометр. Напишите формулу для импульсного баланса объема между секциями 1 и 2, и вы увидите соотношение расхода нагнетаемого и уносимого воздуха(1Р и IVe).в секции 2 поток хорошо перемешан и скорость постоянна по поперечному сечению, как это было непосредственно перед секцией 1.Сопротивление Pxl можно игнорировать. Также рассчитываются максимальный расход уносимого воздуха и соответствующий размер сопла. 5.
Ламинарные профили скорости потока представляют собой полностью развитые потоки несжимаемой жидкости, которые внезапно расширяются при переходе к трубам большего диаметра, и скорость равномерно распределяется по поперечному сечению. Способ вывода Я Но… Два Рисунок 5. 5.Функция выталкивателя. а-нагнетаемый воздух; Б-увлекаемый воздух; Р = 50 мм воды. Искусство. (Вакуум.) L-пример отношения 5. Это было сделано в 2 часа. При рассмотрении этой проблемы иногда используют формулу (80]. Покажи мне. (1) Ш-1ш- (2) Это выражение ^не только потерянная энергия、 В ламинарном движении формула кинетической энергии-y неверна. *Эта статья рассчитает потери давления за короткое время нагрева exchanger.
Смотрите также:
| Баланс массы | Трубка Пито |
| Уравнение баланса энергии | Расходомер Вентури |
