Оглавление:



Автокорреляция с лаговой зависимой переменной
- Автокорреляция с зависимой переменной запаздывания Предположим, у вас есть модель, чья зависимая переменная берется Если есть задержка в одном периоде, она будет использоваться в качестве одного из объяснений Переменные (удовлетворяющие таким примерам в главе 10).
- В этом случае эффект от автомобиля Корреляция, вероятно, будет оценена нормальной банкротством MNC. по Например, если модель имеет следующий формат: Y = a + RL + RL-1 + «1> (7.30) И предположим, что случайный член ut подвержен автокорреляции Первый заказ: А = ри, -, + е (7.21) Уравнение (7.30) можно переписать в виде: у, = а + р л + р2 ^ ! + День, , + e (7.31) В то же время yt_x зависит от вас и . Это отношения (7.30) /, Это также верно для (/ -1): Дюйм x = os + p, * ,. , + P2d>, 2 + ut_v (7.32)
Поэтому существует систематическая связь с одним из объяснений. Людмила Фирмаль
Первый компонент переменной и случайный член в уравнении (7.31). Chet Оценка смещена, потому что четвертое условие Гаусса-Маркова не выполнено Даже для больших образцов (см. Разделы 3.3 и 3.4). Автокорреляционное обнаружение в модели запаздывания Зависимая переменная Как уже упоминалось в первой статье, J. Дурбин и Дж. Уотсон Дарбин — Уотсон rss содержит переменные, зависящие от задержки.
В этом случае вы можете использовать Используйте L-статистику Дурбина (Durbin, 1970). Это также рассчитывается на основе: Новые остатки. Определяется как * = PVl- / iVar (4) * (7 * 33) Где p — оценка p в автокорреляции первого порядка (7.21). Var (b) -Оценка Дисперсия коэффициентов зависимой от лага переменной. n это число Образец наблюдения.
Примерная оценка p берется из формулы (1-0.5rf), d — нормальная статистика Дурбина – Ватсона, Var (b) — квадрат 227 Стандартная ошибка б. Следовательно, A можно рассчитать на основе нормальных результатов. оценка регрессии ТАТ. В большой выборке A распределяется как N (0,1), то есть как нормальное распределение Переменная, равная единице со средним 0 и дисперсией ноль Гипотеза о том, что нет автокорреляции.
- В результате появилась гипотеза об отсутствии автомобилей. Корреляция может быть отклонена на уровне значимости 5% для абсолютных уровней. Если значение больше 1,96 и на уровне 1%, 2.58, при применении двухсторонних стандартов и больших выборок. Основная проблема с использованием этого теста n Если Var (b) больше 1, невозможно рассчитать A.
Альтернативная процедура применения тестов с использованием коэффициентов запаздывания Диапазоны перечислены в Приложении 7.2 и используют зависящие от лагов Переменные как пояснительные переменные не влияют на результаты.
Как приятно А-тест, эта процедура применима только к большим образцам. Людмила Фирмаль
Когда в число объясняющих переменных входит зависимость задержки Использование переменных, метод Кокрейна — Оркатта может привести к локали R. Betancourt и X. Kelejan (Betancourt, Kelejian, 1981) и L. Oxley и C. Roberts (Oxley, Roberts, 1982). Для этого В этом случае рекомендуется использовать сетку при построении модели.
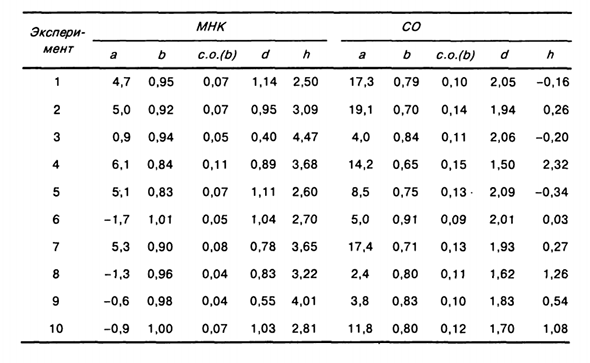
Хилдрет — Ищите Лу или похожие методы. упражнения 7,10. Эксперимент Монте-Карло, модель у, = а + р ^ , + и 1) Использование OLS; 2) Использование метода Кокра on — Orcatta (CO), в то время как истинные значения a и P равны 10 и 0,8. Подвергается случайным членам и начальной автокорреляции Заказ: И = rc, , + e „ Где р равно 0,7, а значение е равно 5 вместо 5.
Зависимые значения нормально распределенных случайных величин Ожидаемое значение и единица измерения слева. Этот эксперимент был проведен 10 раз с образцами из 30 наблюдений. снова Результаты приведены в таблице. Значение а представляет собой оценочное значение а. B- О степени P; (B) -Стандартная ошибка b \ d ^ / -Durbin — Статистика ватт Сон;
А — это статистика Дурбина. 1. Опишите метод, построенный с использованием регрессии Традиционные МНК указывают на наличие автокорреляции. 2. Теперь объясните результаты автокорреляции оценок OLS Модель. Результат оценки регрессии от 3. Ответьте на вопрос OLS (2) или дайте противоречивый Улучшение оценок, полученных с помощью Кокрановского метода Orukatta.
Смотрите также:
Если вам потребуется помощь по эконометрике вы всегда можете написать мне в whatsapp.

