Пример решения задачи №45.
Автодрезина ведет равноускоренно две платформы массами 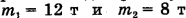 . Сила тяги, развиваемая дрезиной,
. Сила тяги, развиваемая дрезиной, 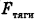 = 1,78 кН. Коэффициент сопротивления движению
= 1,78 кН. Коэффициент сопротивления движению 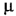 = 0,05. С какой силой
= 0,05. С какой силой 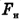 натянуто сцепление между платформами?
натянуто сцепление между платформами?

Решение:
Рассмотрим силы, приложенные к платформе массой 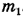 . На нее действует сила тяги дрезины
. На нее действует сила тяги дрезины 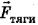 , сила тяжести
, сила тяжести 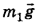 , сила реакции опоры
, сила реакции опоры 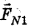 , сила сопротивления
, сила сопротивления 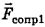 и сила натяжения
и сила натяжения 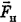 .
.
На вторую платформу действуют сила тяжести 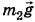 , сила реакции опоры
, сила реакции опоры 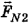 , сила натяжения сцепки
, сила натяжения сцепки 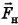 и сила сопротивления
и сила сопротивления 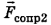 (Рис. 10-19).
(Рис. 10-19).
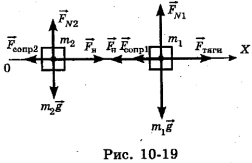
Подчеркнем, что силы реакции опоры и силы сопротивления, действующие на каждую платформу в отдельности, различны, потому что у платформ разные массы. А вот силы натяжения 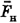 , действующие на обе платформы со стороны одной и той же сцепки, по модулю одинаковы, поэтому мы их обозначили одной и той же буквой
, действующие на обе платформы со стороны одной и той же сцепки, по модулю одинаковы, поэтому мы их обозначили одной и той же буквой 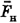 , хотя приложены они к разным телам и направлены противоположно друг к другу.
, хотя приложены они к разным телам и направлены противоположно друг к другу.
Согласно второму закону Ньютона, записанному в векторной форме для первой платформы,
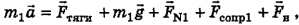
а по модулю с учетом того, что сила тяги 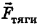 анти-направлена силам
анти-направлена силам 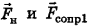 и численно превосходит их, так как вектор ускорения платформы сонаправлен с вектором силы тяги,
и численно превосходит их, так как вектор ускорения платформы сонаправлен с вектором силы тяги, 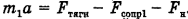
Для второй платформы второй закон Ньютона в векторном виде 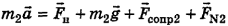 а по модулю, поскольку вектор силы натяжения
а по модулю, поскольку вектор силы натяжения 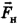 теперь сонаправлен с вектором ускорения второй платформы,
теперь сонаправлен с вектором ускорения второй платформы,
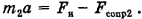
Мы получили два уравнения с двумя неизвестными: ускорением а и силой натяжения 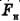 (силы сопротивления
(силы сопротивления 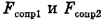 не будем считать неизвестными величинами, так как определить их достаточно просто). В этой задаче ускорение определять не требуется, поэтому исключим его из равенств (1) и (2). Для этого достаточно разделить равенство (1) на равенство (2) (напомним, что левые и правые части уравнений можно соответственно складывать, вычитать, делить и умножать, если это требуется по ходу решения задачи, и от этого равенство между левыми и правыми частями этих уравнений не нарушится). При делении не известное нам ускорение а сократится, и мы получим уравнение с одним неизвестным
не будем считать неизвестными величинами, так как определить их достаточно просто). В этой задаче ускорение определять не требуется, поэтому исключим его из равенств (1) и (2). Для этого достаточно разделить равенство (1) на равенство (2) (напомним, что левые и правые части уравнений можно соответственно складывать, вычитать, делить и умножать, если это требуется по ходу решения задачи, и от этого равенство между левыми и правыми частями этих уравнений не нарушится). При делении не известное нам ускорение а сократится, и мы получим уравнение с одним неизвестным 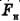 , которое нам требуется определить:
, которое нам требуется определить:
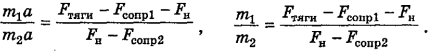
Выразим силу натяжения FK из последнего уравнения, проделав необходимые алгебраические преобразования:
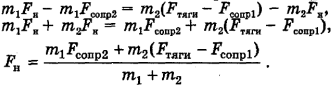
Теперь запишем формулы сил сопротивления 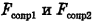 :
:
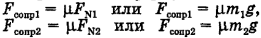
и подставим полученные выражения в формулу силы натяжения:
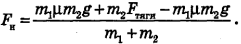
Выполнив приведение подобных членов, получим окончательно
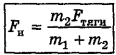
Мы видим, что величина силы натяжения сцепки не зависит от сил сопротивления движению платформ. А вот если бы нам требовалось определить ускорение, с которым движется эта система, то, выполнив необходимые действия и определив его из уравнений (1) и (2), мы убедились бы, что его величина от сил сопротивления, действующих на платформы, зависит (для определения ускорения а теперь следовало бы сложить попарно левые и правые части уравнений (1) и (2). При этом сила натяжения FK сократилась бы при приведении подобных членов и осталось бы одно уравнение с одним неизвестным ускорением а).
Переведем все единицы в СИ: 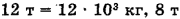
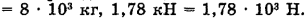
Подставим числа и произведем вычисления:
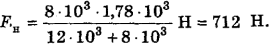
Ответ: 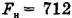 Н.
Н.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:

