Астатический гироскоп

Астатический гироскоп

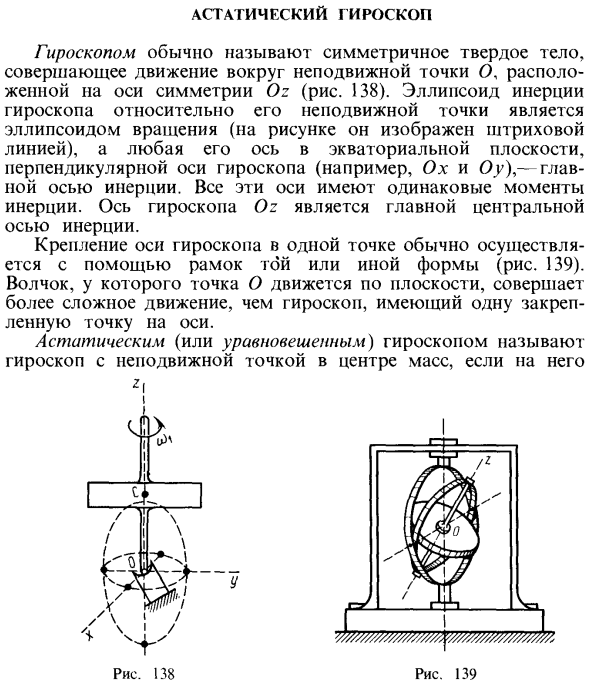
• Гироскоп обычно называют симметричным твердым телом, которое движется вокруг неподвижной точки O на оси симметрии Oz (рис. 138). Инерционный эллипсоид гироскопа относительно неподвижной точки является сфероидом (показано пунктирными линиями на рисунке), а оси экваториальной плоскости, перпендикулярные оси гироскопа (например, Ox и Oy), являются главными осями инерции. Все эти оси имеют одинаковый момент инерции. Ось гироскопа Oz является главной центральной осью инерции.

Ось гироскопа фиксируется в одной точке с помощью какой либо формы рамы (рис. 139). Верхняя часть, где точка O движется вдоль плоскости, движется сложнее, чем гироскоп с одной фиксированной точкой на оси. Астатический (или сбалансированный) гироскоп это гироскоп с фиксированной точкой в центре масс. Только реакция между гравитацией и фиксированной точкой будет работать. В астатическом гироскопе есть комбинация двух случаев: интеграция Эйлера и интеграция Лагранжа. Если Oz является осью симметрии гироскопа, если ось координат зафиксирована на гироскопе Oxyz, если Jx = Jr стационарный гироскоп, то главный момент внешней силы относительно неподвижной точки A O (n ) = 0, Рисунок 140 Без силы.

Для того чтобы система уравнений распалась на отдельные независимые уравнения, выражения потенциальной и кинетической энергий не должны содержать членов с произведениями переменных. Людмила Фирмаль

Это связано с тем, что реакция между гравитацией и неподвижной точкой проходит через эту точку трения в неподвижной точке (рис. 140). Из теоремы об изменении момента движения абсолютного движения гироскопа относительно фиксированной координаты Момент движения для неподвижной точки гироскопа равен Ko = const. В частности, постоянная величина является модулем момента движения Ko. Если одна из фиксированных координатных осей Ozx ориентирована вдоль вектора моментов движения Ко, направление которого не изменяется в пространстве координатных осей, Проекция Ko на ось O является главной осью инерции точки O и одновременно осью вращения самого гироскопа, AL = tfocos9, Где 9 угол между осью Ozx и соответствующей осью вращения Oz. Э

то указывается так же, как угол главы. В дальнейшем выясняется, что он есть. С другой стороны, ось Oz является главной инерционной осью гироскопа в фиксированной точке O, поэтому K. = J. A .. так J.o) j = ^ 0 cos9 и cos9 = J. (Оз k0. (20) Определить сбалансированное движение гироскопа. То есть при заданных начальных условиях устанавливается временная зависимость угла Эйлера , 9 p. Поскольку L = 0, L1X = L ^ = = ( = 0. Учитывая это и условие симметрии Jx = Jf, мы получаем следующее динамическое уравнение Эйлера: J ^ + (J Jx) мм = 0; x dz y ^ + (J y) (oo) = 0; Вам нужно приложить к ним уравнения движения Эйлера oh = sin 0 sin p + 6 cos p; 0j, = sin 0 cos q —Osin p; (22) CO2 = COS0 + p. Удобнее использовать первый интеграл этой системы вместо системы уравнений (21). Один получается умножением (21) на ooh, ay, o2 и сложение соответственно.

• После преобразования Jx (кокс + oJ) + J. s = const = 2h (23). Это соотношение первый интеграл системы (21) представлено константой 2L и представляет закон сохранения механической энергии T + IJ = h. Где P постоянная, равная потенциальной энергии минус ноль. Если вы добавите каждое из системных уравнений (21), умножив каждое на Jx (ox, Jy ny, Jzaz), вы получите еще одно начальное интегрирование после интегрирования. ^ ( Ооо + уу) + Jz 0; = const = K . (24) Соотношение (24) является законом сохранения момента движения для неподвижной точки. Другое первое интегрирование следует из третьего уравнения (21) системы. сотрудничество. = const = co (0), (25) Где o (2O) это значение o2, когда = 0. Первый интеграл (23) (25) системы уравнений (21) можно использовать вместо самой системы уравнений.

Если мы заменим o2 на ω 0 и рассмотрим Ko = const, мы увидим из (20), что угол раздела является постоянной. конечно cos 0 = Jz ( lKo = const = cos 0O, Где 0O это значение 0 при z = 0. Поскольку 0 = const, угловая скорость перемещения главы равна 0 = 0. С учетом этого система уравнений (22) принимает вид: yuh = f sin 0O sin p; (o = sin0Оcos р; а) о, = фСО50о + ф. (22 ) Добавьте первые два уравнения этой системы, возведя их в квадрат. получить o2 + co, = 2sin20О (sin2 р + cos2 ) = 2sin20О. (26) Когда мы определим величину o2 + u2 из (23), мы проверим, что она постоянна. co2 + o2 = (2h J2 a z012) Jx = const. (27) Учитывая (27), из (26) 2 = (ω + o2) sin20О = const, То есть угловая скорость прецессии = const = 0 и, следовательно, Ф = Фо + Фо.

Только в уравнение для системы вместо координаты х входит обобщенная координата д, вместо массы — коэффициент инерции а, а вместо жесткости с0 следует взять коэффициент жесткости с. Людмила Фирмаль

Где 0 и 0 угловая скорость прецессии и угол прецессии в первый момент. Из (22 ) видно, что угловая скорость его собственного вращения также постоянна, учитывая (25) и (28). = r010) 0cos0О = const = 0 (29) Таким образом, ф = фо + фо, (29 ) Где 0 и 0 постоянные значения. Движение гироскопа с собственной скоростью вращения f, постоянной скоростью прецессии f и постоянным углом нутации 0 называется нормальной прецессией. Таким образом, в общем случае сбалансированный гироскоп будет выполнять регулярную прецессию за счет инерции вокруг направления момента движения Ko.

Чтобы сбалансированный гироскоп регулярно прецессировал из за инерции, то есть без воздействия момента внешней силы на его фиксированную точку, должно быть выполнено условие LF = (Л Л) ФсО80. (30) Условие (30) получено в 3 этой главы. Продолжайте из (29). Если , и 0 не удовлетворяют этому условию, внешняя сила должна быть приложена к гироскопу для поддержания регулярной прецессии. Когда сбалансированный гироскоп информируется о начальной угловой скорости coo вокруг соответствующей оси вращения, момент движения гироскопического Ко всегда направлен вдоль этой оси без изменения направления.

В этом случае угол нутации равен нулю и соответствующая ось Вращение совпадает с осью прецессии, куда направлен момент движения и поддерживает постоянное направление в неподвижном пространстве. Эти оси гироскопа также не меняются в направлении этого пространства. Эта характеристика сбалансированного гироскопа широко используется в различных устройствах гироскопов, таких как гирокомпас и автопилот, потому что она не меняет направление, например, далекие звезды. Теория аппроксимации гироскопа учитывает, например, влияние кратковременных возмущений, действующих на гироскоп из за движения монтируемого объекта при кратковременном ускорении.

Смотрите также:

Задачи по теоретической механике

Кинематические уравнения Эйлера	Движение гироскопа под действием силы тяжести
Задача о вращении твердого тела вокруг неподвижной точки. Случаи интегрируемости	Приближенная теория гироскопа