Оглавление:
Асимптоты графика функции
Построение графика функции значительно облегчается, если знать его асимптоты. Понятие асимптоты рассматривалось при изучении формы гиперболы (см. с. 81).
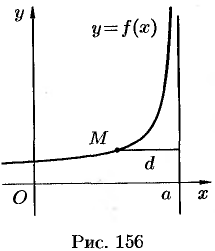
Напомним, что асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 156).
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят, что прямая 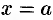 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если
, если 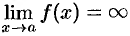 , или
, или 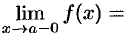
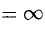 , или
, или 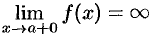 .
.
Действительно, в этом случае непосредственно из рисунка 156 видно, что расстояние точки 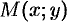 кривой от прямой
кривой от прямой 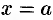 равно
равно 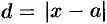 . Если
. Если 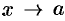 , то
, то 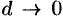 . Согласно определению асимптоты, прямая
. Согласно определению асимптоты, прямая 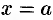 является асимптотой кривой
является асимптотой кривой  . Для отыскания вертикальных асимптот нужно найти те значения
. Для отыскания вертикальных асимптот нужно найти те значения  , вблизи которых функция
, вблизи которых функция  неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
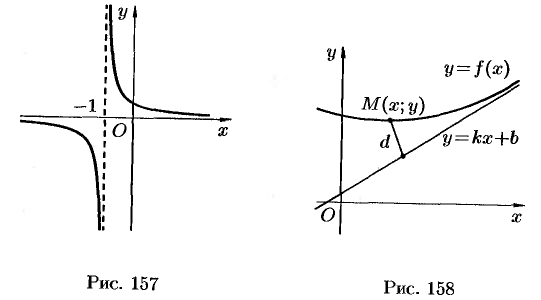
Например, кривая 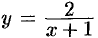 имеет вертикальную асимптоту (см. рис. 157)
имеет вертикальную асимптоту (см. рис. 157) 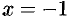 , так как
, так как 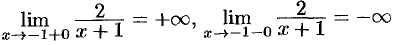 .
.
Уравнение наклонной асимптоты будем искать в виде

Найдем 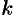 и
и  .
.
Пусть 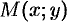 — произвольная точка кривой
— произвольная точка кривой  (см. рис. 158). По формуле расстояния от точки до прямой
(см. рис. 158). По формуле расстояния от точки до прямой  находим расстояние от точки
находим расстояние от точки  до прямой (25.5):
до прямой (25.5): 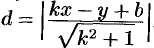 .
.
Условие 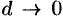 будет выполняться лишь тогда, когда числитель дроби стремится к нулю, т. е.
будет выполняться лишь тогда, когда числитель дроби стремится к нулю, т. е.

Отсюда следует, что 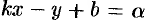 , где
, где 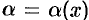 бесконечно малая:
бесконечно малая: 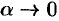 при
при 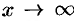 . Разделив обе части равенства
. Разделив обе части равенства 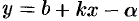 на
на  и перейдя к пределу при
и перейдя к пределу при 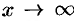 , получаем:
, получаем:
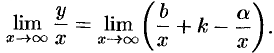
Так как 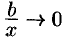 и
и  , то
, то

Из условия (25.6) находим  :
:

Итак, если существует наклонная асимптота 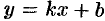 , то
, то 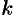 и
и  находятся по формулам (25.7) и (25.8).
находятся по формулам (25.7) и (25.8).
Верно и обратное утверждение: если существуют конечные пределы (25.7) и (25.8), то прямая (25.5) является наклонной асимптотой.
Если хота бы один из пределов (25.7) или (25.8) не существует или равен бесконечности, то кривая  наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
В частности, если 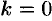 , то
, то 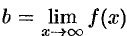 . Поэтому
. Поэтому 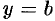 — уравнение горизонтальной асимптоты.
— уравнение горизонтальной асимптоты.
Замечание: Асимптоты графика функции  при
при  и
и 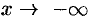 могут быть разными. Поэтому при нахождении пределов (25.7) и (25.8) следует отдельно рассматривать случай, когда
могут быть разными. Поэтому при нахождении пределов (25.7) и (25.8) следует отдельно рассматривать случай, когда  и когда
и когда 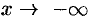 .
.
Пример №25.13.
Найти асимптоты графика функции 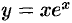 .
.
Решение:
Так как  , то график функции при
, то график функции при  наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
При 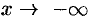 справедливы соотношения
справедливы соотношения
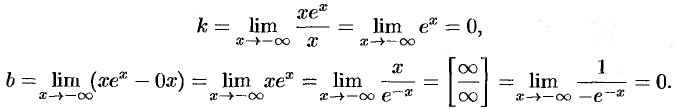
Следовательно, при 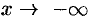 график имеет горизонтальную асимптоту
график имеет горизонтальную асимптоту 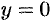 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Наибольшее и наименьшее значения функции на отрезке |
| Выпуклость графика функции. Точки перегиба |
| Общая схема исследования функции и построения графика |
| Функции двух переменных |

