Оглавление:




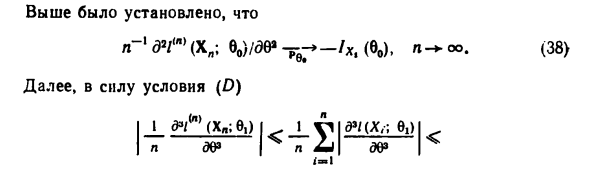





Асимптотическая нормальность оценок максимума правдоподобия
- Рассмотрим повторение независимой выборки, Модель должна быть непрерывной для наглядности. 8 (n) (xn) Богатые корни уравнений правдоподобия d / (n) (xn; 6) / ab = 0. (ЗС) Положи на любой биб, 6> 0 Точный смысл утверждения о целостности корня 1) (n) (x „) Наверное нигде не понятно Статистика 8 (n) (xn), i = 1, 2, …, с любой волной 6> 0 Существует ограничение отношений (См. Пункт 2). Чтобы быть точным, мы можем представить это Каждое измеренное значение Re в основном Подмножество B (в пределах e% и ограничений этого подмножества, уравнение верно Вероятность C0) имеет корни в интервале (8-6, 8 + 6). В этом случае, если 6> 0 достаточно мало,
линейная идея Линеаризовать и найти уравнение C0) вблизи любой точки 8 Изменить приближенное решение этого уравнения Для любого числа, напишите линейно согласно формуле Тейлора Левая аппроксимация уравнения C0): dim (* \ e) a («W, e») + d * 11n) (x «; e) (e_6) + a (X.a.e) + (E6 39 dV dV * Для xеe BeJ удалите оставшуюся часть C1), Приближенное решение уравнения C1) 6 oo LG (0, 1) в качестве предела. Многие правила относятся ко второму фактору в C4) (См. Теорему Хинчина, пункт 1) и С3), Вероятность сходится к 1.
Поэтому статистика Для 6 («‘(x 正常; 6 °) Pe, LG асимптотически нормально (80, (IXt (80) x) ЗДЕСЬ)). Людмила Фирмаль
Следовательно, последовательность статистики 6 <n) (xn; 8), n = = 1, 2, …, причем каждый фиксирован в зависимости от параметра Исправлено 6 статистик 8 <n) (xn; 8) асимптотически нормальных # (8, (/ *, (8) n) ~ ‘) Относительно Pe. Тем не менее, Мера Re ‘^ LPe Статистика b «(n) (xn; 8) Качество как 0 рейтинг. Таким образом, ни один из подсчета 245 Статистика 9 <n) (xn; 6), 8e6 не подходит в качестве оценки параметров Параметр 6. Здесь помните обо всей веб-статистике. 8 (n) (xn; 6) «близок» к оценке площади Be’.v по построению
Уравнение максимального правдоподобия 8 (n) (xn). Мы можем сказать это Статистика 8 <n) (x „) аппроксимирует весь набор статистики § <n) (xn; 6), 8eE, индивидуальная статистика 8 («‘(xn; 8) -Pv-мера переменной xn домен Близко к одному. Точное значение этого утверждения следующее: Сходимость при фиксированной 8oS0 вероятность (C (n) (Chl) -eo) / (e (i) (chl; wo) — C5) Докажем С5) Закономерность: (D) Существует третья производная по плотности 8 {(x; 8), \ d4 (Xi; 8) / ab3 | <A (x,), MwL (X,) <oo, ve = e, Где h (x ) — функция, независимая от 8.
- Напишите левую часть, чтобы доказать связь C5) Разложение уравнения правдоподобия C0) частичным уравнением Тейло Квадратичные условия от Тейлора: a / (n) (xa; eo) Покровительство Согласен * Покровительство С6) Где 8i = 8i (xn; 8) между и в. Уравнение 6 (n) (xn) Рассмотрим C0) C6) и C2) — В , ; ео) -ео) (i + [± Был установлен на нем l dCh1p) (Hya;% Кроме того, в соответствии с условием (D) -p — ^ — / x, (b0), -J- J] A (X.) — * — * Const, α- + oo. C9) Из согласованности C7), C8), C9) и оценки 8 (x „) C5). Принимая во внимание лемму 2, Результат. Теорема 3. Информация Фишера ht (b) и 8ev положительны, условия (A) и (C) выполнены, (С), (D).
Напишите в формуле Тейлора в условиях теоремы из (n> (xn; e> = av (n) (xn; en) + (in_e ajn (xn; ep D0) ae »ae» Назначено D0) согласованный корень 6 = 6 (n> (xn) уравнений Используя вероятность C0) и (/)) | 1 | ay (l) (xn; e (l) (xn)) дБ * с того времени N -h h (X.) — p- * const, 8 (n> (Xl) —80 — = — * 0, n- * oo, Затем, применяя лемму 2 к правой части D1), мы можем заключить, что: n-1 (xn; e (l) (xn)) / ab «-l ^ / (l) (xn; eo) / ae» — ^ o, i Отсюда и С8) / r1 (xn; e (n> (xy)) / ae * — * / x, F), D2) Отношение D2) для меня достаточно большое Множество вероятностей P0, сколь угодно близких к 1, имеет вид
Во-вторых, непротиворечивая оценка уравнения Максима Метод максимального правдоподобия асимптотически нормальный N (8, (/ x, (8) i)). Людмила Фирмаль
Справедливое неравенство d2 / <»> (x„; e <»> (xn)) / a2 <0, То есть последовательный маршрут 6 (х „) уравнения правдоподобия Фактически это локальный максимум функции f (n) (xn; 6). Кроме того, если пη) (xn), b2A) (xn) два последовательных маршрута Уравнение правдоподобия, функция / (| 1) (xn; 6) является константой Конец b1H> (xn), Of * (xn) или на отрезке между 247 Точка 6s (n) (xl)> — локальный минимум функции ftn) (xn; 6). В последнем случае, очевидно, 0. D3) Корень уравнения правдоподобия vzp> (xn) равен Богатый «Между маршрутом 0 (n) (xy) и Oj ^^ xJ, Последовательный, от D2) и D3) x.hi »о Однако это противоречит предположению / *, F)> 0, 6 e 6. Были получены следующие результаты: Теорема 4. Предположим, что условия теоремы выполнены.
Теорема 3 и производная df (x; 6) / 58 не исчезают точно так же То же самое применимо, если между значениями нет интервала. п — * — оо, и reprobabilities, которые, как правило, объединяются в виде произвольной функции Вероятность имеет один внутренний локальный максимум До 6 <n) (xn), что является асимптотически нормальным Оценка обычных параметров N (c, (/.v, F) n) to ‘) c. Вывод 1. Функция правдоподобия f (n) (xn; 6) Когда максимум достигается во внутренней точке, применяется теорема 4 Оцените максимальную вероятность. Вывод 2.
Сделать φ (8) дифференцируемым параметром Ф’F) # 0 с параметрическими функциями. В условиях теоремы 3 Используя лемму 3, заключаем, что ΦF (n) (xn)) асимптотически нормальна. Нормальный H (φ (8), φ ‘(8J (/ x, (8) n) ~’). ΦF) можно инвертировать. Затем выберите φ = φ (8) в качестве нового параметра. Получить функцию правдоподобия с новой параметризацией = / ()) (Xn; 6), F (c)) / ar) Следовательно, оценивается значение уравнения правдоподобия φ (n) (xn) dbn) (xn; φ) / df = 0 соответствует оценке φ (8 (n) (xn)). Независимый вывод об асимптотической нормальности последней оценки. 6 (n) (xn) — наибольшая оценка Возможность, максимальная оценка в условиях теоремы 4 Вероятность φ (8G1) (xn)) асимптотически нормальна # (φ @), φ ‘
Смотрите также:
| Преобразование статистик | Асимптотическая эффективность оценок максимума правдоподобия |
| Асимптотическая нормальность выборочных квантилей | Асимптотическая достаточность |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

