Оглавление:
Арктангенс
а) Арктангенс числа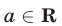 
(обозначается 
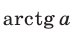) — это такое число 
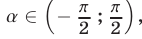тангенс которого равен а, т. е.
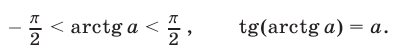
б) Для любого 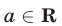справедливо равенство
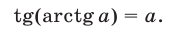
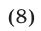
в) Равенство
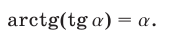
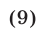
является верным только при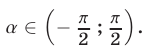 
г) Для любого 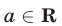справедливо равенство
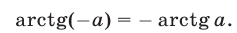
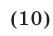
д) Таблица значений арктангенса:
Примеры с решениями
Пример №51.
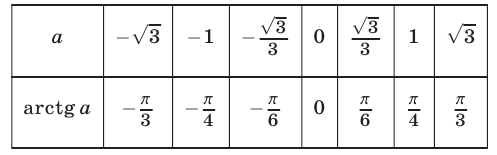
Вычислить:
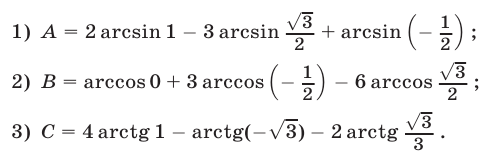
Решение:
1) Используя таблицу значений арксинуса, получаем
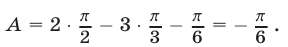
2) С помощью таблицы значений арккосинуса находим
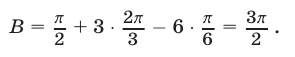
3) Используя таблицу значений арктангенса, получаем
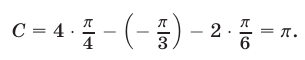
Ответ.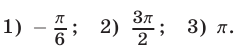
Пример №55.
Вычислить:
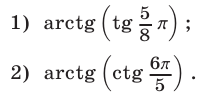
Решение:
1) Так как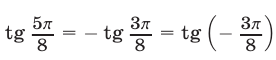 
и 
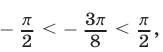то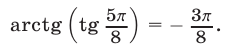 
2) Используя равенства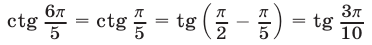 
и учитывая, что 
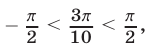получаем.
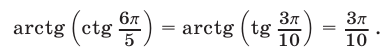
Ответ.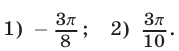 
Пример №56.
Вычислить:
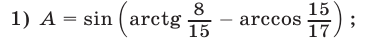
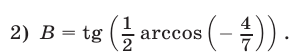
Решение:
1) Пусть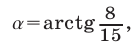 
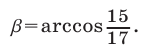Тогда 
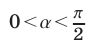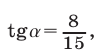
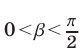и 
и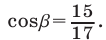 
Воспользуемся формулой
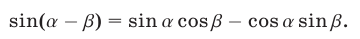
Так как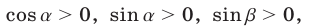 
то
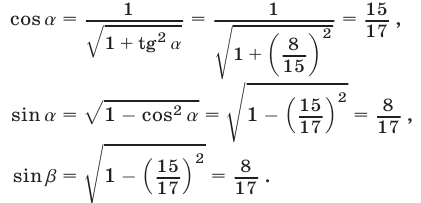
Следовательно,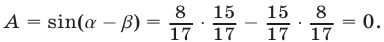
2) Пусть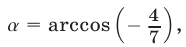 
тогда 
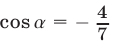и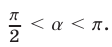 
Используя формулу 
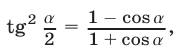получаем
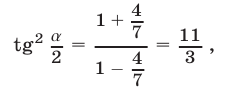
откуда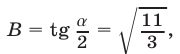 
так как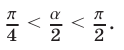 
Ответ.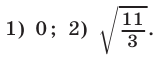 
Пример №57.
Доказать, что
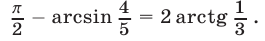
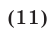
Доказательство. Пусть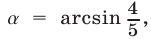 
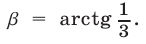Заметим, что 
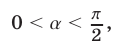откуда 
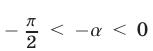и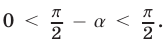 
Далее, так как 
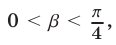то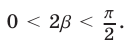 
Итак, углы 
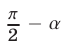и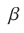 
заключены между 
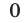и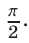 
Поэтому для доказательства равенства 
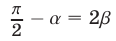достаточно показать, что какая-нибудь тригонометрическая функция (например, тангенс) каждого из этих углов имеет одно и то же значение. Докажем, что
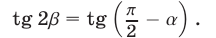
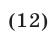
Так как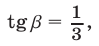 
то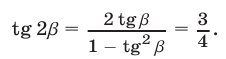 
Пользуясь формулой 
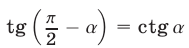и учитывая, что 
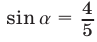и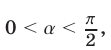 
находим 
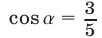и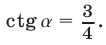 
Итак, равенство (12) является верным и, в силу сделанных выше замечаний, справедливо равенство (11).
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Арксинус с примером решения |
| Арккосинус с примерами решения |
| Числовые неравенства примеры с решением |
| Уравнение и его корни. Преобразование уравнений |
