Арифметические и алгебраические корни n-й степени
Определим понятия арифметического и алгебраического корней n -й степени. Пусть 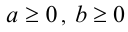 — действительные числа, n — натуральное число, большее или равное 2. Число b называется арифметическим корнем n -й степени из числа а , если
— действительные числа, n — натуральное число, большее или равное 2. Число b называется арифметическим корнем n -й степени из числа а , если
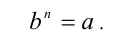
Обозначение: 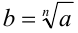 . Например, арифметический корень 2-й степени из числа 4 равен 2:
. Например, арифметический корень 2-й степени из числа 4 равен 2: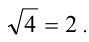 Заметим, что некоторые авторы допускают в определении корня n -й степени значение n=1, т.е. полагают
Заметим, что некоторые авторы допускают в определении корня n -й степени значение n=1, т.е. полагают 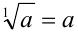 . Однако на практике корни 1-й степени обычно не используются, поэтому в данном пособии мы будем придерживаться ограничения
. Однако на практике корни 1-й степени обычно не используются, поэтому в данном пособии мы будем придерживаться ограничения 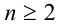 (так же, как, например, в [1,2]).
(так же, как, например, в [1,2]).
Расширим понятие арифметического корня до понятия алгебраического корня. Снимем ограничения на неотрицательность а и b . Пусть теперь 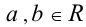 . Число b называется алгебраическим корнем n-й степени из числа а , если
. Число b называется алгебраическим корнем n-й степени из числа а , если 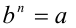 . Таким образом, алгебраический корень нечётной степени n оказывается определён и для отрицательного а .
. Таким образом, алгебраический корень нечётной степени n оказывается определён и для отрицательного а .
Например, 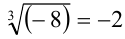 , так как
, так как 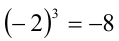 . Приведём без доказательства две теоремы.
. Приведём без доказательства две теоремы.
Теорема 1. Для каждого неотрицательного числа а существует единственный арифметический корень n-й степени (совпадающий при этом с алгебраическим корнем n -й степени).
Теорема 2. Для каждого отрицательного числа а существует единственный алгебраический корень нечётной степени (который также отрицателен).
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

