Оглавление:














Аналогия между переносом импульса и тепла
- Осборн Рейнольдс указал на сходство процессов передачи тепла и импульса в 1874 году. Его работа приводит к удобным, простым отношениям. Свяжите коэффициент теплопередачи, коэффициент сопротивления и коэффициент массопередачи. Улучшения в этих отношениях были получены Прандтлем(1910) и Тейлором(1916).У нас есть Рассмотрим выводы, которые приводят к отношениям Прандтля-Тейлора. Мерфи(1932) и Кармэн (1939) развили это исследование дальше.1 в соотношении — это имя карман. Недавно За эти годы были сделаны дальнейшие модификации, в том числе работы Рейхардта (1940), Коултера, Мартинелли и Йонассена (1941), Мартинелли(1947), Лиона (1951) и Деслера. (1954) x.
В этой книге мы не будем подробно рассматривать вывод отношений более сложных, чем уравнение Прапптля — Тейлора. Уравнение теплопередачи можно легко обобщить на случай Массоперенос; это делается в ребята. 35, массоперенос в турбулентном движении. Аналогия Рейнольдса. Рейнольдс сказал, что в обмене тепла или импульса между жидкостью и жидкостью、 Процесс переноса твердой стенки определяется 2 механизмами.1 эти уравнения рассматриваются Якобом [74] и Кнудсеном и Кацем[85]. 2) вихрь, вызванный видимыми движениями, которые перемешивают жидкость и постоянно приводят новые частицы в контакт с поверхностью.
Поэтому в рассмотренном случае можно применять тот же закон, что и для сопротивлении, включенных последовательно, в электротехнике. Людмила Фирмаль
Первый взнос Рейнольдс считал жидкость зависимой от природы, а вторая была функцией скорости жидкости вдоль поверхности. Эти дополнительные комбинированные эффекты приводят к уравнению теплопередачи. Он написал в форме I разность температур между поверхностью и жидкостью. p-это плотность. V-средняя скорость. А и в-константы. I-количество тепла, передаваемого на единицу измерения Время, проходящее через единицу площади поверхности. Рейнольдс записал сопротивление движению I, вызванное трением жидкости, в виде I = A’NJ. Где A ’ и B также постоянны.
Соображения, которые Рейнольдс не назвал, привели к предположению, что A-A и B пропорциональны A ’и B’.Значение Рейнольдса, записанных в Яр Обозначение системы с развитым турбулентным потоком эквивалентно коэффициенту теплопередачи a, а величина B ’пропорциональна коэффициенту сопротивления/.Рейнольдс. а претендует на соразмерность. Идеи Рейнольдса были развиты другими исследователями и выражены в математической форме в виде уравнений, связывающих а и/. 2 для рассмотрения. Основной способ получить это уравнение.
Метод основан на пропорциональности передачи тепла и импульса, а 2-й метод основан на уравнении теплового и импульсного потока (количества Движение.)Пропорциональная зависимость между теплопередачей и передачей импульса может быть представлена 4 переменными, которые мы определяем в случае движения жидкости в трубе. Средняя температура составляет 1b, труба нагревается при температуре 1L.
Эти 4 величины делятся на (а) тепловой поток от жидкости к стенке трубы и(1b- / 8) ккал г м-ч * е ’ кг-м / ч (б) — импульсный расход стенки трубы, у; (в) емкость накопителя энергии, которая может передаваться в единицу времени, если тепло передается параллельно стенке Труба, (g) _ число перемещений в единицу времени, параллельных стенке трубы, кг. Тогда мы предполагаем, что между этими величинами существует следующий процент: (a)_© (*) *из этого можно найти формулу a = ^коэффициента теплопередачи. (25.17) 13 было показано, что напряжение сдвига стенки t связано с коэффициентом Сопротивление / уравнение (25.18) поэтому уравнение (25. 17) .
Объедините и получите формулу, известную как аналогия Рейнольдса Выведенный Рейнольдсом: __ / ioCp 2(25: 19)2-й метод для получения этого уравнения имеет полутеоретическую основу и изучается после рассмотрения в следующем разделе Применение теории путей смешения. Турбулентная теплопроводность и путь перемешивания. Ваш 13, следующее уравнение, посвященное турбулентному движению(13. 37). Полное напряжение сдвига m * x с богатой скоростью gradients. In это уравнение кинематической вязкости V зависит только от молекулярной структуры жидкости, но Uv является турбулентным Вязкость, которая определяется движением fluid. As показано, что сумма зависит от соотношения.
За счет перемешивания растений Левски I и связан с градиентом скорости. Аналогичное значение известно как турбулентная теплопроводность. Рассмотрим движение жидкости, показанное на рисунке. 25. 3.Вот 2 скорости и температуры Плоскость разделена на расстоянии, равном пути смешивания. Предположим, что движение жидкости между этими плоскостями происходит со скоростью, равной среднему значению времени / / Соблюдать абсолютное значение пульсационной составляющей скорости.
Энергия переносится частицами жидкости, и ее расход через область Эдди Пэлла равен массовому расходу× В произведении удельной теплоемкости определено, что абсолютные значения Uy и xx пульсирующих компонент скорости в какой-то момент времени имеют одинаковое среднее значение. Формула (13. 40) дается для этих величин через смешанный проход: / ı1= 1Н/§/.Разница температур / Uy \ pCp [I ( _ ^ «)] * * hl-обозначено _ * * * — » — Y * 14%I (1 (1\ r) g тепловой поток, обусловленный турбулентным движением жидкости. / а рис. 25.3. Роль пути путается§CP12 принимает форму 1 — ^ — I. знание теплопередачи Прантля I ay I \ aU / TurbuLeitz 0M Поток. Эта формула включает в себя формулу.
Если такая же сумма попадает в уравнение турбулентности Теплопередача, opa, называется турбулентной теплопроводностью и обозначается ai. Поэтому тепловой поток, обусловленный турбулентностью, может быть описан в следующем виде: Теплопроводность Фурье(19. 1) может быть описана с использованием молекулярной теплопроводности. ч(25. 20) запишите уравнение, которое представляет собой количество тепла, передаваемого Жидкость в процессе одновременного возникновения теплопроводности и турбулентного перемешивания приобретает a = _bCp (a + ae)^, (25.21), аналогичное приведенному выше уравнению.
На основании полученных выводов Кинематическая вязкость турбулентного потока и теплопроводность турбулентного потока равны. Хотя экспериментальные дапны показывают, что это единственная истина Приблизительно, предположение о равенстве часто проводится в теоретических исследованиях. Вывод формулы обеих величин основан на предположении, что частицы жидкости проходят через Отдайте X компонент смешивания на расстояние и равное расстояние, а также их избыток тепла и импульсов. Это, вероятно, на самом деле не реализовано, но это не лишено смысла. Предположение о том, что истинное количество передаваемого тепла и импульса отличается в той же степени, что и идеальное выражение.
Мы имеем дело с проблемой переноса массы. В дальнейшем будет уместно описать уравнение массопереноса компонента а при движении двойной смеси. А =-(^ в + /> лвв)^ — (25.22) эта формула содержит коэффициент молекулярной диффузии IIA и BAVE ниже коэффициента диффузии турбулентности, мы показываем, что BAVE является P | ^и/^|, с выводом, аналогичным тому, который был описан выше для AB. И так оно и есть.、 В теории смешивающего пути Awe, ae и\равны. Вывод аналогии Рейнольдса из теории турбулентного переноса. уравнения, связанные с a и/(25.19), были получены на основе пропорций Для интуитивного considerations.
Можно также оценить из уравнений турбулентного переноса тепла и импульса, и этот вывод, вероятно, более информативен. Необходимо определить окончательный дефект выражения. Опишите уравнение (25.21) для жидкости, охлаждаемой радиальным теплопередачей в трубе. Расстояние Формула (25.21) имеет вид A = ecr («+a. It принимает форму -^. (25.23) все величины, содержащиеся в этой формуле, относятся к среднему значению времени.
Аналогичное уравнение, содержащее только среднее по времени, описывается для потока импульса. Полное напряжение сдвига действующее в осевом направлении поверхности па Жидкий элемент в виде цилиндра будет равен: m = p^ -/ -^)^. (25.24) когда коэффициенты молекулярной миграции a и V считаются незначительными, но сравниваются с коэффициентами турбулентности、 Выражения (25.23)и (25.24) могут быть записаны с выделением E / y в виде YY ^ CpLs cn_A Oye X.
Изменение m как в ламинарном, так и в турбулентном радиусах равно 1.Турбулентная теплопередача генерируется таким же образом, как и передача импульса、 Тогда мы предполагаем, что плотность теплового потока следует той же зависимости. o_A y(25.26) из этих 2 формул видно, что на всех расстояниях от оси отношение X является постоянным(l). Удобнее всего использовать его значение на стене. Следовательно,-может быть представлен, но (P. In большинство уравнений теплопередачи, значение которых-непосредственно понимается Плотность теплового потока стены.
Поскольку это отношение является постоянным, уравнение (25.25) может быть интегрировано, принимая yy *-за Интеграл интеграла. Интеграция(ПЯ Измените значение стенки на значение той точки жидкости, где усредненное по времени значение скорости равно средней скорости. Кроме того, температура жидкости в это время Она совпадает со средней температурой (температурой смешивания).Затем предположим равномерное распределение давления по поперечному сечению 1. {Примечание Под Ред. Знайте, что скорость стенки ила равна ) Обнулить. Далее (а), есть -.Таким образом, получаем уравнение (25.19)/ÜeCpaa-уравнение, которое сводится к 2. 25.
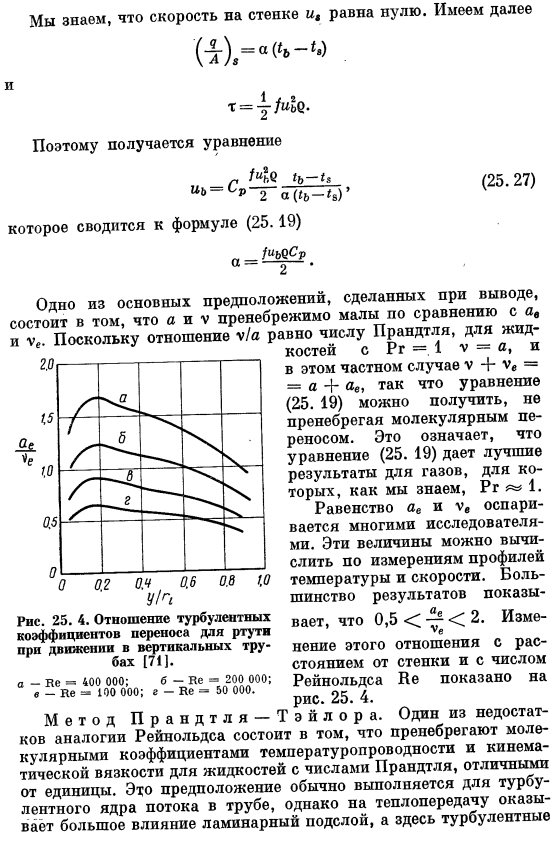
Одно из основных допущений, сделанных в заключении、 что a и V ничтожно малы по сравнению с a и V. Так как отношение 1a равно числу Прандтля, то для жидкости r T = 1 V-a, P 25. 4.Коэффициент коэффициента турбулентности Перенос ртути при движении по вертикальной трубе[71]. А-бэ = 400,000; б-Ке = 200,000; в _ Кэ =■100,000; Р-Ке = » 50000.В данном конкретном случае это V + В= а + ае. Что?! Формула (25.19)может быть получена без пренебрежения молекулярным переносом. Это означает, что уравнение (25.19) дает наилучший результат для газа в Pr l * 1, Как известно. Равенство АЭ и УФ обсуждается многими исследователями.
Эти значения могут быть рассчитаны на основе измерений профиля температуры и скорости. Большинство результатов показывают, что это 0,5 2. Изменение этого соотношения из-за расстояния и числа Рейнольдса от шага не показано на рисунке 25.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Расчёт найти определения | Учебник |
- Пренебрегая молекулярными коэффициентами температуропроводности и кинематической вязкости жидкостей с числами Прандтля, отличными от 1. Обычно это предположение выполняется. Однако в случае турбулентного ядра потока в трубе ламинарный подслой оказывает существенное влияние на теплообмен, при котором коэффициент турбулентности снижается до нуля, а молекулярный Коэффициенты A и V не могут быть исключены из рассмотрения. Метод Прандтля-Тейлора является попыткой преодолеть этот недостаток. В основном, используются следующие методы Напишите уравнения Рейнольдса аналогия для ламинарного подслоя и турбулентного ядра теплового уравнения.
Затем, обычным способом расчета последовательного сопротивления из этих Уравнение получает единственное выражение импеданса. Схема течения в кольцевой трубе показана на рисунке. 25. 5.Предположим, что поток жидкости нарушен, как показано ниже. Рисунок, 2 вида движения. направление теплового потока b7 a 25. 5. Прандтль-блок-схема для получения уравнений Тейлора. а-турбулентное ядро; б-слоистый подслой. е- Труба wall.
Твердое вещество таких материалов не позволяет воздуху приходить в состояние движения ют разности температур, а тем самым и предотвращает передачу дополнительного количества тепла конвективными токами. Людмила Фирмаль
Ламинарный подслой, мы предполагаем, что все тепло, поступающее из зоны турбулентности, проводит к стенке, потому что скорость очень мала. Следовательно, тепловой поток в ламинарном потоке Подслои равны (» -*»). (25.28) поток импульса этого слоя равен (25. 29).Распределение тангенциального напряжения круговой трубы определяется стратифицированным подслоем m = m *(1-n»)、 Очень тонкий,1 и t t8.Следовательно, формула(25. 29) переписывается в виде интегрирования этого отношения к толщине B стратифицированного подслоя и берется оттуда, где толщина A определяется как (25.30).
Вместо tvT_ _ 2ЧЧ введите / используя формулу (25.18).Подставляя эту формулу в Формулу (25.28), получим формулу теплового потока ламинарного подслоя:(25. Тридцать одна) Предположим, что передача тепла и импульса в турбулентном ядре следует аналогии Рейнольдса. Импульс, передаваемый в единицу времени параллельно оси трубы、 Зона турбулентности простирается до стенки трубы, как и ожидалось при выводе уравнения (25.19).Однако если турбулентное ядро окружено слоистым подслоем, то избыток Движение, которое перемещается каждую единицу времени параллельно границе ламинарного подслоя, называется RG (ui и.
Поскольку в ламинарном пограничном слое очень мало жидкости, среднее значение Скорость турбулентного ядра и массовый расход IV приблизительно равны средней скорости массового потока и общего потока. Формула (2E.1U) коэффициент теплопередачи a、 Коэффициент теплопередачи только для турбулентного ядра, обозначаемый a. So, процент, который получает выражение a, является отношением a ’ (b-M ’Cp (b — * 0 ((b**)) ’(25.32) где ’ = — — получаем b— u и подставляем формулу (25.18) в ТВ, hb-и {) (25.33) таким образом, тепловой поток равен отношению7 а / из ui & p 2 (ui-u {) (25.34) формулы (25.31) и (25.34) отделить температурную головку I на 2 часа.
Склад если вы добавите эти выражения, вы получите: Форма I A(25. 35), понятно, что можно написать формулу 2. 2 (u—» 1)*#1 $ ’/ u ^ ^ P(25.36) если умножить числитель и знаменатель в правой части этого уравнения на pa / uCp / 2 get / koCp 2 qw’b x x b(25. 37) для жидкости с Pr = 1 используется эта формула(25. 19). Если вы хотите рассмотреть универсальный профиль скорости в разделе 13 US Как видно из рисунка, Мы обнаружили, что в ламинарном подслое безразмерная скорость и+и расстояние от стенки y +равны. 13. 6.It сохраняется до+ + y + = 5 и предоставляет следующий метод. Определите скорость, которая входит в Формулу(25. Как показано, u и+имеют отношение.
Значение u* — это коэффициент сопротивления/ Ниже приводится ссылочная формула(13. 68)] таким образом, вы можете записать η на границу слоистого подслоя. Где u * = 5, и подставляя это выражение в Формулу (25.37),/uOCp1 + 5 v 4 (1) (25) 39)(25.Если вы ставите обе части на Р/Х, это соотношение также можно записать в терминах числа нуссельта: (25. 40) вместо вышеуказанных значений、 Другое выражение. Разница обусловлена наличием переходной зоны между ламинарным подслоем и турбулентным ядром, как показано на рисунке.
Уравнение распределения скорости Экстраполяция турбулентного ядра и ламинарного подслоя совпадает в переходной зоне, где y = 11.6.Поэтому некоторые авторы предложили ввести это значение вместо 5 Знаменатель формулы(25. 40).Другие коэффициенты. Основные усовершенствования в Формуле Прандтля-Тейлора принадлежали карману и предлагали рассмотреть сопротивление теплопередаче. Он состоит из 3 частей. Эти части соответствуют ламинарным подслоям, переходным зонам и турбулентным ядрам. Они показаны на графике универсального профиля скорости на рисунке. 13. 6.Вывод Формула кармана аналогична методу Прандтля-Тейлора.
Для слоистого подслоя(y * 5) уравнения выписываются с учетом температуропроводности молекулы, но они игнорируются Участники турбулентности. Это дает формулу для разности температур ламинарного подслоя. Рассматривая переходный слой (5 30), молекула и Турбулентность transfer. To получаем уравнение кинематической вязкости, вместо термодиффузии оно подставляется в уравнение теплового потока. Эмпирическая формула для распределения скоростей в переходном слое= 5 + 5 1n Интеграл уравнения теплового потока, учитывающий как молекулярную вязкость, так и турбулентную вязкость, вычисляется по формуле Падение температуры переходного слоя.
Наконец, аналогия Рейнольдса используется для получения падения температуры турбулентного ядра (y + ^> 30).Тогда все 3 перепада температур Суммируя, как и в методе Прандтля-Тейлора, получаем формулу для общей разности температур. После деления плотности теплового потока на общее падение температуры、 Следующее уравнение коэффициента теплопередачи:____________2 1 + 5(pg-1 + W tg (25.41) аналогично уравнению Прандтля-Тейлора, это уравнение является уравнением Рейнольдса (25. 19) в случае жидкости c, Pr = 1, большинство результатов можно выразить в общем виде, а в случае молекулы справа-формулой(25. 39) и (25. 41).
Правая часть формулы Рейнольдса (25.19) справедлива, и знаменатель состоит из нескольких членов, которые служат в качестве поправок. Некоторые версии включают элементы, которые учитывают следующие различия Средняя скорость и скорость на оси, и другие учитывают изменение вдоль радиуса T. Исследование Дайслера рассматривает изменения вязкости, обусловленные температурой. Я больше так не делаю. Рассмотрим теоретическое соотношение. Литература, упомянутая в этой главе, содержит информацию о большинстве наиболее важных отношений и других отношений.
Конечное соотношение Но стоит упомянуть эмпирическую формулу, которую Колборн предложил в» / — факторе » [25].Формула — это формула (25. 39) заменить весь знаменатель или (25. 41) формула Pr * 7 * преобразует формулу в обычную форму.(25. 42) величина / называется коэффициентом теплопередачи. Как и другие, это уравнение становится выражением ПР = 1 жидкость Reynolds. It видно, что аналогичная формула существует и для коэффициента массопереноса. Формула Рейнольдса массопереноса изменяется так же, как и Формула В теплопередаче число Шмидта появляется только вместо числа Прандтля number. In в случае массопереноса коэффициент/ — обозначается через / m.
Экспериментально показано, что выражение с коэффициентом /имеет Важное преимущество в описании тепломассообмена. Они использовались не только для труб и плоских пластин, но и для других целей. systems. In в общем, получилось/ я] м. Но Ни/, ни мм не равны, но они все равно равны, когда жидкость обтекает сферическое препятствие или другой тупой предмет obstacle. In эти случаи, полная потеря давления обычно Коэффициент сопротивления чаще всего определяется не сопротивлением трению, а сопротивлением давлению. Если нет сопротивления давлению, то есть Соотношение π=mm = » 2 сохраняется при обтекании плоской пластины и протекании в трубе.
Уравнение коэффициента теплопередачи основано на подобии теплопередачи и передачи импульса. Формула этой аналогии может быть объединена с формулой определения коэффициента сопротивления, которая обеспечивает прямой способ определения коэффициента теплопередачи. Например Аналогию Рейнольдса приводит формула (25.19) / bCp a-2-9.It может быть представлен в виде II = yBePr. (25.43) в гл. 13, удобная формула опыта Определение коэффициента сопротивления при движении в трубе требует использования формулы(13. 72) / = 0.046 существует форма be-0 ′ 8.Комбинация формул (25.43) и (13.72) дает Ui = 0.023 Sun°8Pr.
Эта формула выведена на основе формулы (25.19) и подходит только для Pr = 1, поэтому запишите формулу (25.44) в виде II = 0.023 Be0’8 (25.45). Известная формула Диттуса-Бултера при использовании для жидкости с Pr = 1.To получить выражение числа нуссельта как функцию Be и Pr, можно с помощью следующего выражения: Прандре Тейлор и Калман. Вы также можете использовать эмпирическую формулу в Colborn / — factor. Если вы пишете уравнение Колборна (25.42) в безразмерной переменной、 ’n-2′ Be Pr (25.46) / формула (13. 72), и выражение (25. 46) будет 0.023 быть».1-Быть Pr0 ’83 или N» 1 = 0.023 быть «8 Pr» 38. (25. 47) эта формула Самые распространенные. Задача 25.
Воздух нагревается, который последовательно проходит через ряд прямых стальных труб с наружным диаметром 33 мм и внутренним диаметром 26 мм. Пройдите через прямоугольную емкость с горячей водой. Длина погружной трубы составляет 0,6 м. Средняя скорость газа-15 м! С абсолютное давление Можно считать постоянной величиной и равной 1 Ат.
Если воздух поступает при температуре 16°С, а температура внутренней поверхности трубки считается постоянной и равна температуре воды、 Найти выходную температуру воздуха 99°c 25. 2.Местное выражение(25. 15) на основе формулы нуссельта для среднего числа пластин длины b (25. 16). Число нуссельта турбулентных движений. 25. 3.При температуре 16°C воздух движется по плоской пластине с постоянной температурой поверхности 93°C. Свободный поток 30 м! Вторая пластина имеет ширину 0,6 м и длину 1,2 г.
Рассчитайте суммарный тепловой поток от участка пластины, покрытого ламинарным пограничным слоем, и его части Пластина, покрытая турбулентным пограничным слоем. 25. 4. в случае ae » a мы получаем зависимость между коэффициентом теплопередачи a и коэффициентом сопротивления / потока в трубе. И V. 25. 5.Поток (25. 23) и 25.
Смотрите также:
| Теплообмен при развитом профиле скорости в трубе | Применение анализа размерностей к теплообмену |
| Теплообмен при турбулентном движении. Входные эффекты | Конвективная теплоотдача в трубах круглого сечения |

