Оглавление:








Аналогия между количеством движения и теплообменом
- В предыдущей главе была рассмотрена передача тепла от твердой поверхности к движущемуся потоку за счет совместного действия проводимости и теплопроводности. Convection. In в непосредственной близости от поверхности, он фактически находится в состоянии «единственный способ для покоя и проводимости для передачи тепла» с поверхности t. as расстояние от стенки увеличивается, поток увеличивается, так что поток «переносит тепло» (конвективное) в область x, далее «далек от охлаждения; — — — — становится основным методом теплопередачи»? «Что касается турбулентности, то непрерывное перемешивание жидких частиц связано с колебаниями турбулентной скорости.
Это смешивание приводит к теплопередаче при наличии градиента температуры в stream. So, помимо теплопроводности Т, 3-й тип теплообмена наблюдается еще больше на Туре с несуществующим потоком! Конвекция, связанная с объемным движением 1gyoy7zh1schostost7’p турбулентность Смешивание мало изучено, поэтому никому не удалось предсказать картину теплопередачи турбулентности на основе некоторых расчетов. ■С другой стороны, путь, указанный Рейнольдсом, Прандтлем, Тейлором и фон карманом, может быть использован для получения формулы теплопередачи из гидродинамических измерений и глубокого проникновения в турбулентный механизм теплопередачи.
Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела {\displaystyle Y}Y и способа теплообмена между телами. Людмила Фирмаль
Основные положения этого раздела будут разработаны на основе идей прандкара по аналогии Рейнольдса и ламинарных подслоев. В следующих разделах описываются последние достижения в области расчета турбулентного теплообмена. Только слой жидкости в непосредственной близости от стенки оказывает существенное влияние на теплообмен. Вектор скорости этих слоев параллелен стенке, а тепловой поток перпендикулярен стенке. Wall. So, учитывается закон теплопередачи в потоке, параллельном стенке (в направлении оси x). Предполагается, что скорость изменяется практически только в направлении y direction. In в этом направлении также происходит теплообмен.
Поэтому существенное изменение температуры происходит только в направлении у. Согласно Прандтлю, ламинарный ламинарный поток без турбулентного перемешивания существует в непосредственной близости от стенки, и фактические условия упрощаются, предполагая, что теплопроводность и трение оставшегося ламинарного потока в потоке малы и незначительны по сравнению с турбулентным теплопередачей. В любой плоскости, параллельной поверхности стенки и, следовательно, параллельной оси x, возникает напряжение сдвига в подслое ламинарного течения. Дю.
Согласно формуле (2-2), тепловой поток на единицу площади плоскости определяется следующим образом: Далее рассмотрим плоскость, параллельную стенке в условиях турбулентности. Из-за смешанного otic и движения, жидкие частицы постоянно проходят через эту плоскость. На рис. 8-1 показана плоскость aa, в единицу времени, в единицу времени, от плоскости 1-1, с взвешенным количеством жидкости m, проходящей вверх, скоростью и температурой/. Это количество жидкости переносится на плоскость 2-2. (В стационарном режиме такое же количество жидкости m движется от плоскости 2-2, скорость равна u, а температура сдвигается в плоскости/ -/.
Частицы жидкости несут количество тепла, равное m’cₚt, и частицы движутся вниз. M’cpt ’. Для/>/’, тепло передается через единицу площади за единицу времени (/- Д) (8-1/: Рис. 8-1. Упрощенная схема турбулентного обмена* •Однако, частицы жидкости обладают кинетической энергией. Если скорость и скорость больше u’, то частицы жидкости выше плоскости aa получают ускорение от частиц, движущихся вверх, а частицы ниже этой плоскости замедляются. Из-за такого турбулентного обмена, разница между скоростями и И И и небольшое. Турбулентное перемешивание действует аналогично напряжению трения b в плоскости aa.
Это является основанием для введения понятия «виртуальное турбулентное напряжение сдвига». В соответствии с законом импульса, который сформулирован в разделе 6-2, это виртуальное напряжение сдвига. Общее турбулентное напряжение трения равно увеличению или уменьшению импульса за счет обмена массы т жидкости за единицу времени. Таким образом, в случае турбулентного напряжения трения уравнение = (И-и ’). (8-2) Если неизвестная величина m ’исключается из уравнений (8-1) и (8-2), то получается следующая зависимость между турбулентным тепловым потоком и напряжением сдвига: т-В.
- Это выражение также может быть записано в дифференциальной форме. = (8-3) Потому что положения плоскостей 1-1 и 2-2 являются необязательными. Это соотношение было впервые получено Рейнольдсом в 1874 году, поэтому его назвали аналогией Рейнольдса. Если соответствующее отношение получено для плоскости ламинарной путем деления 2-го отношения, приведенного в начале этого раздела, на первое отношение, то: dt. 7 = — т Дю. ’ (8-4) Отношение теплового потока к напряжению трения Тот же закон применяется для турбулентных или ламинарных течений Мистер поток. Л (8-5) Или x _; _rg_1. Л а (8-6).
В жидкостях или газах с критерием Прандтля 1 теплопередача в ламинарном или турбулентном потоке связана с напряжением трения по тому же уравнению. * В потоке пограничного слоя желательно получить зависимость между объемом стенки (tw, u = 0) и внешним краевым потоком пограничного слоя (/ₛ, uₛ). Это соотношение для жидкости y. Pr = 1 получается интегрированием уравнения (8-3) в пределах границы (слоя**) поскольку толщина пограничного слоя тонкая, 8-за qfx и соотношение постоянно рядом, интеграция приведет к следующим: Для полной стабилизации потока в трубе необходимо использовать среднюю скорость um и объемную температуру tb. In в этом случае для трубы получаются следующие зависимости: л. ля. = т ы. ———• / о) ш р он Если умножить обе стороны этого уравнения на площадь поверхности стенки трубы a, то получим: т. Где r-сопротивление (r = xw / 4). (8-7).
Это простое соотношение между величиной теплопередачи qw и сопротивлением r справедливо только для среды с критерием Прандтля, равным 1. Людмила Фирмаль
Для всех газов значение критерия Прандтля несколько отличается от единицы с известным значением сопротивления, поэтому формула (8-7) всегда дает правильное представление о силе теплопередачи. Сопротивление может быть заменено энергией, которая должна быть потреблена для прохождения газа через трубу. Значение сопротивления трубы r при перепадах давления определяется dr равным dr (lsr / 4), а объемная скорость газа v =uₘ (nd2! 4). Следовательно, требуемая энергия необходима для течения、 Вт = ВБП =ruₘ. Теперь мы находим отношение количества тепла, переданного этой энергии (8-8) ■>э Эта важная зависимость указывает на то, что при уменьшении скорости уменьшается энергия, необходимая для обеспечения скорости и удельной теплопередачи. Эта ситуация используется в самолетах охлаждения или теплообменников.
Система охлаждения окружена каналом, который замедляет поток воздуха перед входом в охладитель, а увеличение давления за счет замедления движения воздуха снова ускоряет движение. Такой канал Кулер показан схематично. 8-2. Канал охлаждения-рисунок 8-2. Конструкция воздуховода, сплиттер авиадвигателя-в настоящее время разрабатывается широко. Применяемый в авиационной промышленности, он также используется в высокоскоростных локомотивах и вагонах, но мощность, необходимая для обеспечения движения охлаждающего оборудования в воздухе, может быть очень мала. Однако это увеличение не является бесплатным, поскольку чем медленнее воздух проходит через систему охлаждения, тем больше площадь поверхности для обеспечения отвода предписанного количества тепла.
Те же отношения. При проектировании парового котла необходимо учитывать размеры поверхности и необходимую мощность. Если необходимо уменьшить массу и габариты котла за счет облегчения прохождения горячих газов в котел, то этого следует добиваться с помощью более дешевых источников энергии. В котлах velox эта проблема решается с помощью газовой турбины. Газовая турбина приводит в действие воздуходувку для подачи воздуха в печь. Пример 8-1. Воздух течет со скоростью 1 м в длину и 20 мм в диаметре 30 м / с. Температура воздуха на входе в трубу составляет 20°С, давление-1, 0 кг / см2. Перепад давления в трубе составляет 81, 2 мм воды. Искусство. Или 80 кг / см2. Количество тепла, отдаваемого трубе воздухом, если стенка трубы нагревается до температуры/ w = 100°c; В первом приближении значение критерия Прандтля для воздуха составляет 0, 72, но можно использовать результаты расчетов по формуле (8-7).
Сопротивление труб движению воздуха Количество тепла, передаваемого в воздух, определяется из уравнения 9. 81 и 0, 24. Qw = 0. 025-ed — — — — — — — (tw — = 0. 002 (tw-tb) ккал / с-град- = 0. 002-3 600 (/ᵤ, — fb) ккал / ч-г рад—ТБ) ккал / ч-г рад Температура стенки трубы / tsu = 100°c средняя температура ТБ неизвестна. Количество тепла, передаваемого в воздух, также можно рассчитать по формуле Где Р-удельный вес воздуха (Р = 1, 29 кг / м * при 20°С и 1, 0 кг / см2). Tₜ-температура на входе в трубу. Fₑ-средняя интегральная температура при выходе из трубы. Если вы установите число в последнее выражение, вы получите следующий результат: 0. 0004 л. : Кя = 1, 29. 0, 24. 30-hj — — — — — (fₑ -/.) = = 0. 003 (/e-ккал / сек-град. Средняя температура головки d / w = — выше tb Случай 1-4 — это d / w = d (d ^ — f-d / e) / 2. Температура стенки считается постоянной.
Отсюда Выровняв правую часть последних 2 уравнений, вы можете увидеть, что 0. 002 a [tw—————— = 0. 003(tₑ-tj. Коэффициент a не может быть определен с помощью таблицы. 1-2, соотношение неизвестно. Предположим, что a = 1. Тогда из последнего уравнения получить f = 60°c чтобы найти значение a, можно воспользоваться равенством От 100 до 20. Тг » 100-60′ И Следовательно, со стола. Найти 1-2 l = 0, 96. Весь расчет обеспечивает только первое приближение, поэтому вам не нужно повторять его, чтобы найти новое значение a. Затем определите количество тепла, которое будет передано В. = 0. 003(60-20)■3 600 = 430 ккал} ч * °c; Точный расчет по формуле, описанной в следующем параграфе, дает результат, превышающий результат, найденный в 15u.
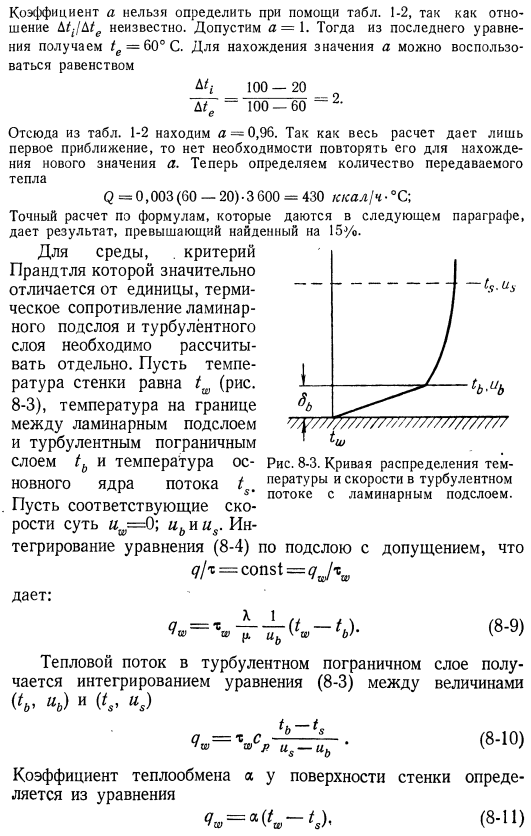
Что касается окружающей среды. Тепловое сопротивление ламинарного и турбулентного слоев должно рассчитываться отдельно. Сделайте температуру стенки равной tw (рис. 8-3), температуру границы между ламинарным и турбулентным пограничными слоями tb и температуру основного потока core/ be. W = = 0; вы и you. So. .Рисунок 8-3 .Турбулентные кривые распределения температуры и скорости с ламинарными подслоями . q ^ = Интеграл уравнения (8-4) на подслое с предположением, что const = qjtw Дай.
Тепловой поток в турбулентном пограничном слое определяется величиной (» .Он получается путем интегрирования уравнения (8-3) между «B) и (*, «₅) .^ = ^ ^ 7 — (8-10) Коэффициент теплопередачи у стенки а выражается формулой (8-ч) Если уравнение (8-9) — (8-11) решается относительно Вытяните напорную головку, а 3-й-1-й и 2-й, и так далее .1+( «&/» $)(Пр-1) Откуда ?(8-12) Эта формула выражена в терминах л .Прандтля (1910 и 1928) [L .98] и Дж .Тейлора (1916) .
Смотрите также:
| Точные решения уравнения энергии ламинарного пограничного слоя | Движение жидкости в трубе |
| Движение жидкости в трубе | Продольное обтекание плиты |

