Оглавление:


Предмет теория автоматического управления тау
| Условия устойчивости линейных систем автоматического управления | Устойчивость нестационарных систем |
| Алгебраические критерии устойчивости | Методы оценки качества регулирования линейных систем |
Анализ устойчивости по логарифмическим частотным характеристикам
- Анализ стабильности логарифмической частотной характеристики В инженерной практике широко используется анализ устойчивости систем автоматического управления, основанный на использовании логарифмических характеристик открытых систем. Это в основном связано с тем, что построение логарифмических частотных характеристик открытых систем, особенно асимптотических логарифмических частотных характеристик, значительно проще, чем построение годографов амплитудных и фазовых характеристик.
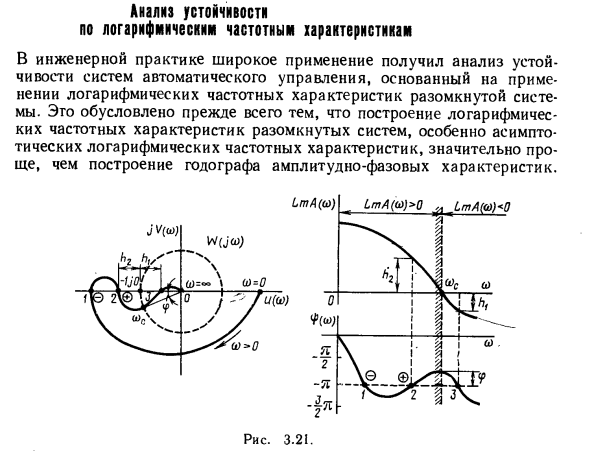
Рисунок 3.21. Покажем требования, которые должны соответствовать логарифмическим амплитудно-частотным характеристикам (LFH) и логарифмическим фазово-частотным характеристикам (LFH) открытой системы, которая стабильна, когда система закрыта. Как показано выше, стабильность связана с числом переходов в амплитудно-фазовой характеристике W (Jm) отрицательного действительного сегмента полуоси (–∞, –1).
Когда амплитудно-фазовая характеристика (Schi) пересекает отрицательную вещественную половину оси, LFK пересекает одну из линий ± 1 (2/1/1). Где i = 0, 1, 2, 3, … (рис. 3.21). Людмила Фирмаль
Если переход через эти линии происходит с правой стороны оттока (-1 / 0), то есть модуль амплитудно-фазовой характеристики равен единице | U7 (/ € o> | <1 и, следовательно, ордината LAH отрицательна Другими словами, LhL (ω) = 20Ig | UP (/ d>) | <0, поэтому отрицательная область LAH не имеет отношения к исследованиям стабильности. Положительный переход (сверху вниз) через интервал (-∞, -1) характеристики W (Ju) находится на пересечении LPC от LhL (ω)> 0 по прямой ± ((2 * + 1) снизу вверх) Соответствующий (точка 2 на рисунке 3.21) отрицательный переход — сверху вниз (точка 1 на рисунке 3.21). Критерий устойчивости Найквиста, применяемый к характеристике логарифмической частоты, может быть сформулирован следующим образом:
Для устойчивости системы автоматического управления разница между числом положительных и отрицательных переходов и характеристикой логарифмической частоты фазы линии ± i (2H-1) требуется. O, 1, 2, … … Lm (co)> 0 во всех областях, где логарифмическая амплитудно-частотная характеристика положительна, равна // 2, где I — число правых корней характеристического уравнения разомкнутого контура система. На рисунке 3.21 показаны, например, амплитудные и фазовые характеристики L AX и LFH, соответствующие разомкнутой системе W (ja>). Эти анализы LAA и LFH показывают, что разница между числом линейных положительных и отрицательных LFH-переходов — Lm / 1 (G))> 0 равна нулю. Таким образом, если открытая система стабильна (/ = 0), закрытая система устойчива, но запас устойчивости по амплитуде равен h {и h2, а запас устойчивости по фазе равен <p.

