Оглавление:
Анализ устойчивости оптимального решения задачи линейного программирования
Важно знать, как изменится решение задачи линейного программирования в процессе изменения ее параметров: коэффициентов целевой функции, элементов матрицы и правой части условий-ограничений. Но особенно важно знать, при каких изменениях параметров задачи ее оптимальное решение остается неизменным.
Изменение параметров задачи линейного программирования может происходить за счет изменения условий функционирования описываемых объектов (например, цены на комплектующие изделия и трудовые ресурсы, стоимости продукции на рынке и т.д.). Эти изменения порождают неопределенность параметров задачи и являются в данном случае детерминированными величинами.
В ряде других случаев параметры задачи линейного программирования являются случайными величинами. И тогда важно знать, как может изменяться решение задачи от реализации к реализации. При этом необходимо иметь, по крайней мере, сведения о математическом ожидании и дисперсии этих случайных величин, если нет возможности оценить их функции распределения. В таком случае для неопределенных значений параметров надо указать соответствующую им доверительную вероятность.
Как правило, в подобных ситуациях для получения ответа решают серию прямых близких задач, изменяя значения параметров.
Особенность задач линейного программирования состоит в том, что полученное оптимальное решение может не меняться при изменении значений параметров в целевой функции и условиях-ограничениях в достаточно широких пределах. Более привычным является «непрерывный» вариант: при небольших изменениях параметров задачи обязательно изменяется и решение — координаты точки оптимума. В этом смысле можно использовать параметрическое программирование, когда определяется поведение решения задачи линейного программирования в зависимости от параметра включенного в выражения коэффициентов целевой функции, элементы матрицы и правой части условий-ограничений. Но эти процедуры даже для одного параметра t громоздки; и его введением не удается описать все возможные изменения параметров задачи. Рассмотрим алгоритм, который позволят определить допустимые множества значений параметров задачи линейного программирования, не приводящих к изменению найденного оптимального решения, и, таким образом указать диапазон изменения каждого параметра.
Имеем следующую задачу линейного программирования (с одним критерием):
найти максимум целевой функции
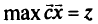
при ограничениях
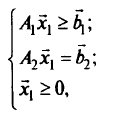
где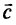 
— вектор, коэффициентами которого являются коэффициенты (параметры) целевой функции; 
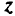— значение целевой функции; 
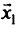— вектор исходных (структурных) переменных; 
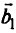и 
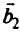— векторы правых часте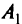й; 
и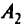 
— матрицы системы ограничений неравенств и равенств.
Для аналитического решения эта задача записывается в канонической форме:
найти целевую функцию
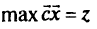
при ограничениях
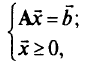
где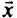 
— вектор, включающий в себя исходные и дополнительные (слабые) переменные; 
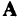— прямоугольная матрица размерности 
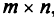, расширенная за счет столбцов дополнительных переменных, превращающих неравенства (2.10) в равенства; 
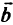— вектор правых частей (объединяет векторы 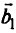и ).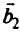
Будем исследовать устойчивость точки оптимального решения задачи (2.9), (2.10), (2.11) в следующих вариантах:
- неопределенность или погрешность содержится только в координатах вектора 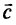целевой функции;
- неопределенность или погрешность содержится только в элементах вектора ;
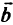- неопределенность или погрешность содержится только в элементах матриц 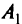и 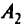(т.е. в элементах матрицы 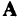, исключая элементы, относящиеся к дополнительным переменным).
Алгоритмы учета других комбинаций неопределенностей основываются на этих случаях.
В дальнейшем будем полагать, что задача линейного программирования решается с помощью симплекс-метода.
Неопределенность в коэффициентах целевой функции. Точка оптимума в симплекс-методе определяется условием
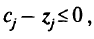
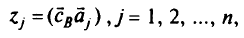
где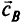 
— вектор из элементов 
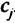относящихся к базисным переменным; 
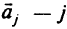-й столбец матрицы .
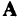Значение целевой функции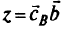 
.
Пусть вместо 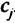имеем значение
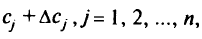
тогда условие оптимума будет определяться величиной
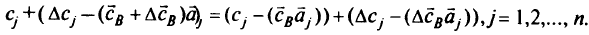
Нарушение условия оптимальности зависит от конкретных зна-чений последнего слагаемого в выражении (2.13): если все
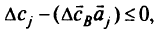
то оптимальное решение не изменяется; при наличии хотя бы одного
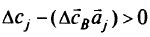
возможно изменение оптимального решения.
Система неравенств
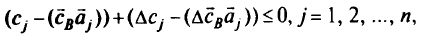
определяет то множество значений элементов
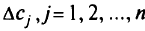
(куда входят и элементы вектора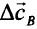 
), которые не нарушают условия оптимума в данной точке.
Пример:
Рассмотрим задачу линейного программирования о выпуске продукции предприятием (см. разд. 2.4). Математическая модель этой задачи имеет следующий вид:
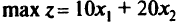
при ограничениях
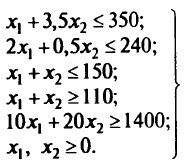
Оптимальное решение задачи приведено в симплекс-таблице:
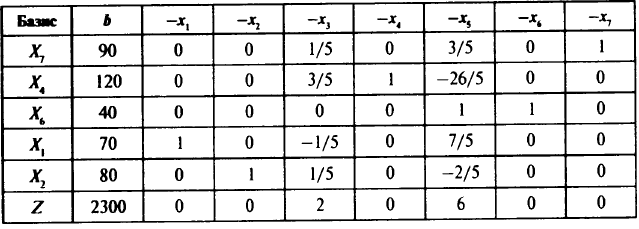
Элементы строки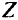 
переменных 
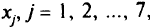взятые с противоположным знаком, и есть значения 
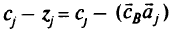, по которым судят об оптимальности решения. Различие в знаках обусловлено правилами заполнения симплекс-таблиц.
Неопределенность имеют коэффициенты исходной целевой функции. Поэтому неопределенность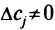 
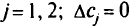для 
для
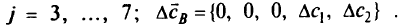
Рассчитаем значения
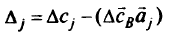
для различных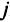 
:
Таким образом, на выбор оптимальной точки в данном случае оказывают влияние только коэффициенты при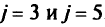 
. Точка оптимума не изменится для тех значений 
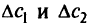, при которых, согласно (2.14),
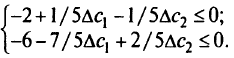
Множество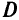 
таких значений представляет собой часть плоскости 
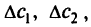заключенную между двумя лучами, выходящими из точки (-10,-20) в направлениях
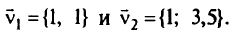
Проблему устойчивости точки оптимума в задаче линейного программирования при неопределенности только коэффициентов целевой функции можно свести к геометрическому аналогу. Плоскость, вектор нормали которой определен коэффициентами целевой функции, в точке оптимума может быть повернута таким образом, чтобы она касалась граней выпуклого многогранника, содержащих точку оптимума.
Диапазон изменения углов поворота плоскости и будет определять допустимый разброс значений коэффициентов целевой функции.
Для удобства все уравнения линейных поверхностей запишем в нормальном (нормированном) виде. Таким образом, мы будем иметь дело с направляющими косинусами плоскостей; в трехмерном пространстве это
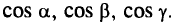
Чтобы определить грани многогранника, содержащие точку оптимума, подставим координаты точки оптимума в ограничения (2.10) и (2.11). Те ограничения, которые выполняются в виде равенств, и определяют искомые грани.
Пусть некоторая гран ь в трех мерном пространстве описывается уравнением
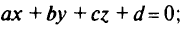
нормальное уравнение этой плоскости имеет вид
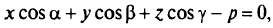
где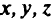 
— текущие координаты; 
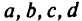— параметры уравнения плоскости; 
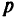— параметр, определяющий расстояние до плоскости от начала координат;
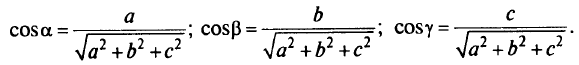
Для плоскости, соответствующей целевой функции с параметрами
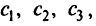
получим
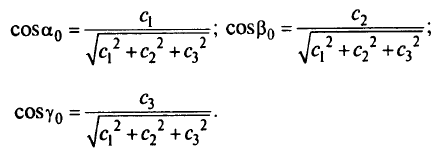
Здесь важны не сами значения 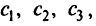, а их отношения:
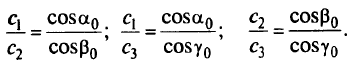
Если некоторая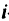 
-я грань многогранника имеет направляющие косинусы
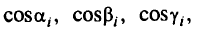
то всякая плоскость, направляющие косинусы которой будут иметь значения между
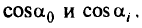
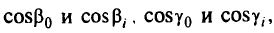
не изменит положение оптимальной точки. Проанализировав таким путем все грани, которым принадлежит оптимальная точка, найдем диапазоны отношений параметров (коэффициентов) плоскости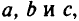 
, которым должны удовлетворять плоскости, проходящие через оптимальную точку и не изменяющие оптимальное решение задачи. Отсюда легко получить возможный диапазон неопределенностей значений коэффициентов целевой функции, не влияющих на решение задачи.
Пример:
Продолжим рассмотрение описанного выше примера.
Определим грани многоугольника, которым принадлежит точка оптимума. Подставим оптимальное решение задачи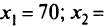 
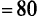в исходную модель (2.15) и найдем, что оптимальная точка есть точка пересечения прямых
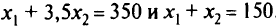
Вектор нормали целевой функции имеет координаты <10; 20}; вектор нормали первой прямой — {1; 3,5}; вектор нормали второй прямой — {1; 1}. С одной стороны, вектор нормали целевой функции может быть повернут до вектора нормали первой прямой, с другой стороны — до второй, т.е. согласно (2.16)
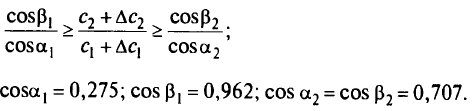
Окончательно условие (2.16) имеет вид
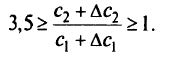
Таким образом, если отношение коэффициентов целевой функции лежит в пределах от 1 до 3,5, то координаты оптимальной точки не изменятся. Полученный результат полезно сравнить с приведенным выше аналитическим расчетом.
Неопределенность только в координатах вектора правой части. При изменении значений правой части исходной системы (2.10), (2.11) в процессе решения изменяются только столбец свободных членов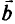 
и значение целевой функции 
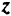. В точке оптимума столбец свободных членов не содержит отрицательных элементов. Таким образом, неопределенность в координатах вектора правой части до тех пор не влияет на оптимальное решение, пока не появятся отрицательные элементы в столбце свободных членов.
Представим матрицу полного ранга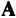 
из (2.12) в виде двух блоков 
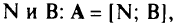, где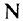 
состоит из небазисных столбцов 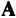, а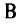 
— из базисных. Аналогично векторы 
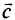и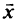 
состоят из базисных и небазисных координат:
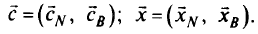
Следовательно, имеем
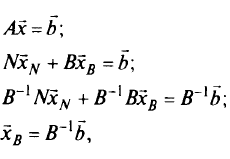
так как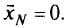 
. Отсюда столбец свободных членов 
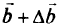на любой итерации может быть получен умножением матрицы 
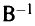на вектор 
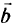в исходной постановке (2.12). Сам же вектор 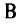формируется из тех столбцов исходной матрицы 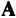(см. 2.12), номера которых на данной итерации определяют базисные переменные. С другой стороны, 
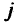-й столбец в матрице 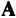, которая после преобразований становится матрицей 
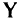, для данной итерации 
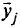имеет вид
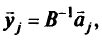
где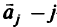 
-й столбец в исходной матрице 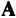из (2.12).
Столбцы матрицы 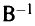— это столбцы тех переменных текущей матрицы 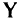, которые были базисными в исходной таблице (как правило, это последние 
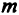столбцов), так как 
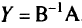, а столбцы 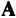, относящиеся к базису исходной таблицы, образуют единичную матрицу, т.е. матрицу 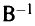мы всегда имеем в процессе решения.
Исходный вектор 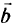и неопределенность его значения 
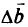задаются. Таким образом, получают новый столбец свободных членов. Если исходный вектор равен 
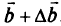, то новый столбец свободных членов
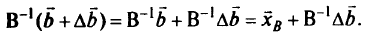
Поскольку в столбце свободных членов оптимального решения не должно быть отрицательных элементов, то условие стабильности примет вид
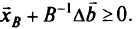
Пример:
Рассмотрим описанный пример в предположении, что исходный вектор правой части
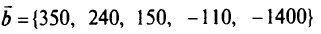
имеет неопределенность
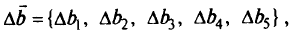
т.е. надо рассматривать вектор
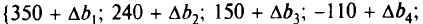
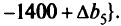
Матрица 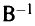занимает пять последних столбцов симплекс-таблицы оптимального решения:
Условие стабильности оптимального решения данной задачи имеет вид:
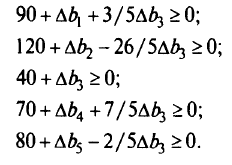
Отсюда находятся те комбинации
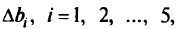
при которых оптимальное решение не изменится.
Неопределенность в элементах матриц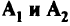 
. Если неопределенность имеет место в отдельных элементах матриц 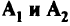, то можно воспользоваться тем, что элементы матрицы 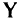оптимального решения определяются через матрицу 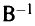и исходную матрицу 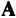из (2.12):
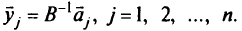
Пусть только один элемент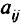 
имеет неопределенность 
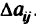. В матрице 
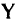оптимального решения получим элемент, имеющий вид
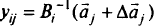
По знаку рассматриваемого элемента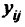 
принимается соответствующее решение.
Этот подход приемлем для небольшого числа элементов матриц, имеющих неопределенность.
Рассмотрим более общий подход. Пусть все элементы матриц 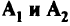имеют неопределенности
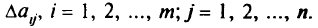
«Перенесем» неопределенности 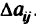в неопределенности правой части. В таком случае надо вычислить неопределенность 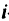-й линейной комбинации
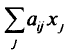
и добавить ее к неопределенности правой части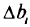 
. Теперь возникает вопрос, каким образом (на основании какой гипотезы) вычислить неопределенность линейной комбинации, и согласно какой гипотезе присоединить ее к неопределенности правой части. От выбора этих гипотез зависит конкретный алгоритм выполнения названных операций.
Рассмотрим два случая. В первом — неопределенность 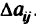является детерминированной величиной (например, показывает изменение цены некоторого ресурса); во втором (в задачах линейного программирования с другим физическим содержанием) — случайной величиной, для которой известны математическое ожидание и дисперсия. Тогда в первом случае неопределенность 
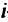-й линейной комбинации 
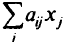будет равна 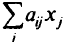а полная неопределенность 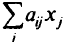-й координаты вектора правой части
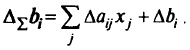
Во втором случае мы будем исходить из того, что все участвующие в расчете неопределенности носят случайный характер и мы можем вычислить дисперсию линейной комбинации, считая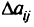 
.
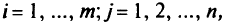
независимыми случайными величинами с известными дисперсиями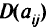 
, а затем суммировать дисперсию линейной комбинации и неопределенности правой части полагая 
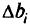равной дисперсии 
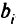т.е.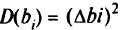 
. Таким образом, дисперсия линейной комбинации
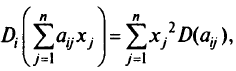
а полная неопределенность (погрешность) 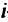-й координаты вектора правой части
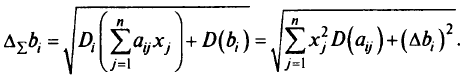
В формулах (2.17) и (2.18) значения
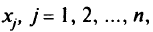
берутся из таблицы оптимального решения. Далее анализируем ситуацию так же, как в случае наличия неопределенности только в правой части. Очевидно, что исследование может проводиться подобным образом и при
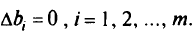
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Задачи о покрытии множества |
| Дробно-линейное программирование |
| Основные направления развития методов решения задач математического программирования |
| Понятие о параметрическом программировании |
