Анализ уравнения Ван-дер-Ваальса.

Анализ уравнения Ван-дер-Ваальса.

• Анализ уравнения ван-дер-Ваальса Для уравнения ван-дер-Ваальса (р + а / V*) (в-б)= РТ ’ «Если вы откроете скобку и расположите полученное значение так, чтобы порядок v был меньше, вы получите уравнение 3-го порядка для определенного объема газа. Пирог? — (ВР + РТ) ый ав-ав-0. Как известно из математики, такое уравнение для заданного значения p и T должно иметь 3 roots. In в данном случае

рассматриваются следующие 3 случая:.1) все 3 маршрута понятны и эффективны. 2) все 3 маршрута реальны и равны друг другу, 3) 1 маршрут реален и 2 воображаемы(сложны). в последнем случае воображаемый маршрут b имеет реальный смысл. • — если вы создадите изотермическую линию, соответствующую уравнению ван-дер-

имеет физический смысл, поэтому только 1 фактический маршрут Людмила Фирмаль

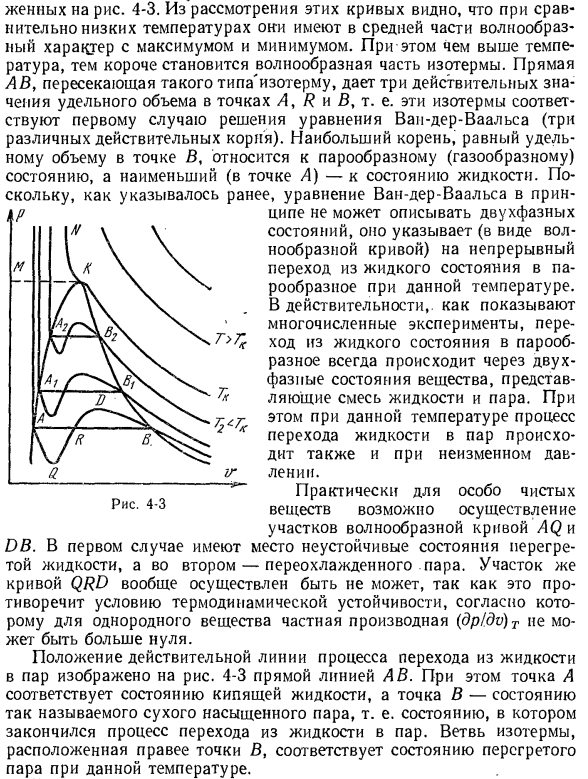
Ваальса в RY-диаграмме, то она будет иметь вид кривой, показанной на рисунке. 4-3.Если изучить эти кривые, то можно увидеть, что при относительно низких температурах центральная часть имеет волнообразные характеристики с максимумом и минимумом values. In кроме того, чем выше температура, тем короче волнистая часть Изотерм. Прямая AB, пересекающая изотермы этого типа, дает 3 вещественных значения определенного объема в точках A,

R и B. То есть эти изотермы соответствуют первому случаю решения уравнения ван-дер-Ваальса (3 различных вещественных корня).Крупнейший маршрут, который равен удельный объем в точке B, обращается в пар (газообразное) состояние и обращается в жидкое состояние минимального (точка а).Как указывалось ранее, ван-дер-Ваальса уравнение, как правило, не может описать 2-фазовые

• состояния, поэтому он указывает на непрерывный переход (в виде волнистой кривой) из жидкого состояния в газообразное состояние при определенной температуре. что переход из жидкого в парообразное состояние всегда происходит через 2-фазовое состояние вещества, которое представляет собой смесь жидкости и пара. Кроме того, при данной температуре, процесс перехода из жидкости в пар происходит

при определенном давлении. На практике волнистые кривые секций AQ и DB высокочистых материалов могут быть realized. In в первом случае происходит неустойчивое состояние перегретой жидкости, а во втором-переохлажденный пар. Часть кривой QRD вообще не может быть реализована. Это объясняется тем, что она противоречит условиям термодинамической устойчивости. Таким образом, для однородного вещества частичная производная (dp / dv)

В самом деле, как многие эксперименты показывают Людмила Фирмаль

m не может быть больше нуля. На рисунке показано расположение фактической линии перехода процесса из жидкого состояния в жидкое. vapor. In в этом случае точка А соответствует состоянию кипящей жидкости, а точка в соответствует состоянию так называемого сухого насыщенного пара, то есть когда переход из жидкости в пар завершен. Ветвь изотермы справа от точки в соответствует состоянию перегретого пара при определенной

температуре. При определенной температуре, называемой критической, изотермы уравнения ван-дер-Ваальса не имеют волнистого сечения. Эта изотерма имеет точку перегиба, а касательная должна быть горизонтальной. Это соответствует 2-му случаю решения уравнения ван-дер-Ваальса, когда все 3 корня вещественны и p ^взаимосвязано (рис. 4-3, точка fC> r). При температуре выше критической (T> 7) изотерма равна 。 ’/Обладает

монотонно убывающим свойством и приближается к кривой в виде гиперболы как температура rises. In эти температуры/, есть 3-й случай решения уравнения ван-дер-Ваальса. Это когда L-корневое действительное число и 2 мнимых числа. Если соединить все точки A, например Alt A 2, то получится кривая, в которой жидкость находится в состоянии кипения. Кривая AK называется граничной жидкостью

curve. So, кривая VC, называемая кривой граничного пара, представляет собой ряд сухих насыщенных паров states. So, для реальных веществ, ro-dnagram можно разделить на 3 характерные области.1) область жидкого состояния слева от граничной кривой жидкости. 2) область 2-фазового состояния (влажный пар), расположенная между жидкостью и кривой границы пара, и 3)

область перегретого пара, расположенная выше критической точки в правой части кривой границы пара. Условно область жидкости была ограничена сверху линией км. Линия км-это критическая Изобара (линия с постоянным давлением, равным критическому). В 1869 году Эндрюс построил настоящую диаграмму Ра, которая впервые была основана на экспериментах с изотермическим сжатием

углекислого газа, и показал характерные линии и области в ней. .- .Поэтому часто реальные цифры называют диаграммами Эндрюса. Остановимся далее на понятии критического состояния материи. Критическое состояние проблемы было диагностировано в 1861 году. И. Он был впервые обнаружен Менделеева. Д. И. Менделеев назвал ее критической температурой. Абсолютная температура кипения, то есть разница между жидким состоянием и состоянием пара, где поверхностное натяжение/натяжение жидкости равно нулю. В. ;Д. И.

Менделеев дал следующее определение: «абсолютная температура кипения означает температуру, при которой частицы жидкости теряют свою когезионную силу (в капилляре они становятся равными нулю, а скрытая теплота равна нулю), независимо от давления жидкость исчезает.»Из анализа уравнения ван-дер-Ваальса, примененного к критическому состоянию, можно получить представление критических параметров относительно констант

уравнений a и b или определить константы a и b известных критических параметров. Если учесть, что уравнения Ван-дер-Ваальса только качественно и правильно описывают поведение реальной материи, то константа awb обычно вычисляется на основе экспериментальных данных. Отправной точкой для получения соотношения между критическим параметром и константой

уравнения ван-дер-Ваальса является то, что в критической точке имеется перегиб к изотермической линии, а касательная в точке перегиба является горизонтальной. Из этого состояния、 Первая частичная производная давления по объему при постоянной температуре (、 ПК = а / 2762,(4-4） Где P / < — давление в критической точке. Если вы получите значения TK и PK из эксперимента, можно найти коэффициенты A и B. 9 Н ^ .. 27 * 2_G? С Рк ЗВТ^»’.К а = =- (4-5） 1-

1 3 8 РК Уравнение ван-дер-Ваальса может быть представлено заданным параметром состояния. Введение относительной величины в уравнение ван-дер-Ваальса вместо переменных p, v и T в / вк =Φ, п / ПК = I и Т / ТК = Т、 Получаем новое уравнение в виде следующего: давление и температура, а также величина а, 6, выраженная в важных параметрах-называется вакуумным объемом. •(i-3 / f2) (3p-1)= 8 м. Полученное уравнение называется уравнением редукции. Эта

формула эффективна для веществ, подпадающих под формулу Ван-де-Ваальса, поскольку она не содержит количества, характеризующего данное вещество. Состояние вещества, находящегося в одном и том же l, f, t, называется соответствующим состоянием. В критической точке все 3 указанных параметра имеют одинаковое значение, равное 1,и критическое состояние всех веществ

соответствует. Если 2 вещества имеют те же 2 параметра, что и 3 указанных вещества, то 3-й параметр этих веществ будет иметь то же значение и вещество будет находиться в соответствующем состоянии. Это явление называется законом каждого государства. Этот закон помогает определить свойства вещества, если известны свойства другого вещества в соответствующем состоянии. Такое

определение свойств вещества называется методом термодинамического подобия. Из соотношения критических точек, полученного из уравнения ван-дер-Ваальса、 РТ ^ Пкпк = 8/3 = 2.67. Это отношение, обозначаемое через / ( * , называется критическим коэффициентом. Уравнение ван-дер-Ваальса должно иметь постоянное значение для всех термодинамически сходных веществ,

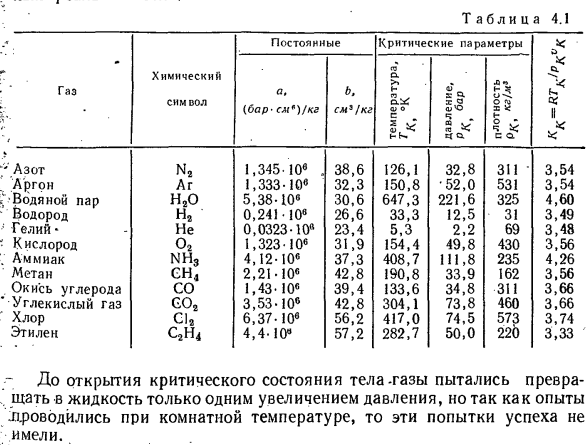
но экспериментальные данные показывают, что величина Кк различных реальных газов является постоянной величиной (табл.4-1).Это еще раз подтверждает, что уравнение ван-дер-Ваальса корректно описывает только качественные характеристики свойств реального тела газа. Таблица 4.1 Постоянные критические параметры* в Химический Р5 О.>, Л•> * О. ГАЗ А, Б. Б га. £о-т ф-、

Знак{бар-см) / кг см3 / кг О.^ О О С; Б 1 их<з£* Часса. N2 азота 1.345 10Э,38.6 126.1 32.8 311•3.54 Аргон АГ 1.333-10Э 32.3 150.8•52.0 531 3.54 Паровая Н20 5.38.10 е 30.6 647.3 221.6 325 4.60 Водород Н2 * 0.24110 е 26.6 33.3 12.5 31 3.49 Гелий * 0.0323-10y не 23.4 5.3 2.2 69 3.48 Кислород O2 1.323-10 * 31.9 154.4 49.8 430 3.56 Аммиак NH3 4.12-Yub 37.3 408.7

111.8 235 4.26 Метан СН4 2.21-10Э 42.8 190.8 33.9 162 3.56 Окись углерода s 1.43-10e 39.4 133.6 34.8 311 3.66 Углекислый газ C02 3.53-106 42.8 304.1 73.8 460 3.66 Хлор с)2 6.37.10 e 56.2 417.0 74.5 573 3.74 Этилен s2n4 4.4.10 e 57.2 282.7 50.0 220 3.33 ′ До того, как было обнаружено критическое состояние, тело пыталось превратить газ в жидкость,

просто увеличив давление в 1 раз, но эксперименты проводились при комнатной температуре, поэтому эти попытки не увенчались успехом. Эксперименты показали, что для того, чтобы преобразовать газ в жидкость, газ сначала должен быть охлажден ниже критической температуры, а затем газ может быть сжижен путем сжатия его вдоль Изотерм. ＃

Смотрите также:

Решение задач по термодинамике

Свойства реальных газов.	Уравнение состояния для реальных газов М. П. Вукаловича и И. И. Новикова.
Уравнение состояния Ван-дер-Ваальса.	Закон сохранения и превращения энергии.