Анализ и моделирование случайной компоненты

Анализ и моделирование случайной компоненты

Целью исследования является выяснение вопроса: подчинены ли ряды некоторому закону или любая их часть случайна? Наиболее простым критерием проверки случайности исследуемого ряда является определение местонахождения максимумов и минимумов. Для применения такого критерия подсчитывают «пики» и «ямы» динамического ряда:

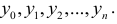
«Пиком» называют значение, которое больше двух соседних. Два или более равных значения, которые больше предшествующих и последующих. Рассматриваются как один пик. «Ямой» называется значение, меньшее двух соседних. Пики и ямы называются экстремальными точками динамического ряда. Число экстремальных точек на единицу меньше числа интервалов монотонности. Интервал между двумя экстремальными точками называется «фазой».

Вычислив число экстремальных точек исследуемого динамического ряда, сравниваем с математическим ожиданием

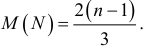
Если их больше, то ряд является быстро колеблющимся. Если их меньше, то последовательные значения положительно коррелированны.

Для оценки существенности разности между подсчитанным числом экстремальных точек и их ожидаемым числом, вычисляем стандартное отклонение (среднее статистическое квадратическое отклонение)

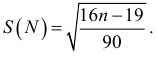
В случайном ряду экстремальная точка приходится примерно на каждые полтора (1,5) наблюдения.

Кроме вычисления числа экстремальных точек, изучают еще и распределение интервалов («фаз») между ними. Для установления наличия фазы длиной 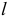рассматривается 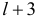уровня динамического ряда, где (для случая роста) первый больше второго, второй меньше третьего, третий меньше четвертого,…, 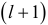-й меньше 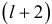-го, а 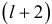-й больше (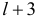)-го. Проверка случайности состоит в сравнении математического ожидания числа фаз различной длины 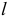и математического ожидания полного числа фаз, вычисленных по формулам

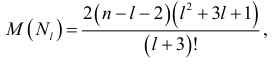
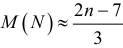
с числом рассчитанных фаз.

Для выявления случайной компоненты динамического ряда применяется также метод конечных разностей, который состоит в вычислении первых, вторых, третьих, …, 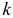разностей, делении на 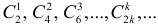и определение момента когда отношение

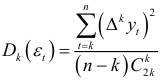
становится постоянным, т.е.

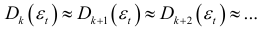
Достоверность равенства

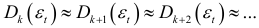
определяется при помощи контрольной величины

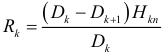
при 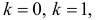… При этом нужно найти такое 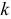, что 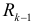, будет надежным, a 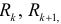— нет. Тогда можно предположить, что 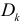будет оценкой для неизвестного рассеяния 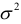случайной компоненты.

Пример 7.6.

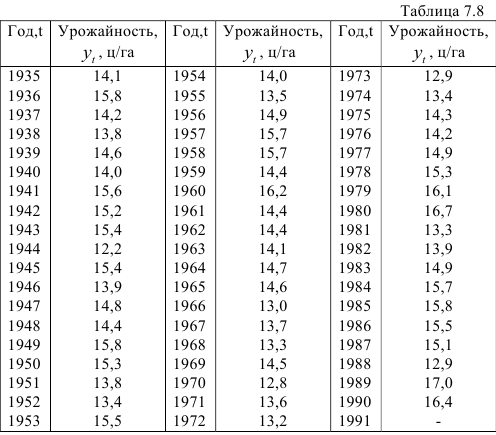
В табл. 7.8 приведены данные об урожайности озимой ржи. Рассматриваемый динамический ряд содержит 56 уровней. Так как дважды встречаются одинаковые уровни (в 1957 и 1958 гг., в 1961 и 1962 гг.), уменьшим число уровней до 54. Анализ динамического ряда показывает, что число экстремальных точек равно 35. Вычисляем математическое ожидание числа экстремальных точек для случайного ряда, состоящего из 54 наблюдений:

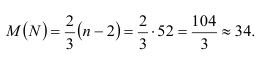
Число экстремальных точек исследуемого динамического ряда и математическое ожидание ожидаемого числа экстремальных точек хорошо согласуются, так как стандартное отклонение

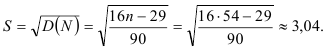
больше, чем разность 35 — 34 = 1. Следовательно, динамический ряд представляет случайную выборку.

Пример 7.7.

Рассмотрим динамический ряд, характеризующий доходы фирмы, производящей детские игрушки:

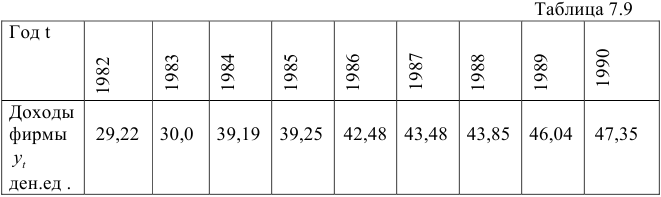
Оценим неизвестное рассеяние случайного элемента 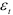, предполагая, что рассматриваемый динамический ряд состоит из гладкой и случайной компонент. Для этого найдем разности 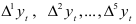. Далее вычислим рассеяние разностей:

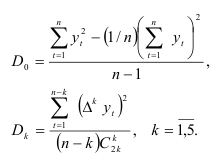
Значения биномиальных коэффициентов приведены в табл. 7.9.

Тогда

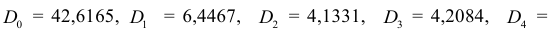
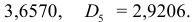
Для необходимых проверок вычисляем

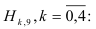
Затем находим контрольные величины:

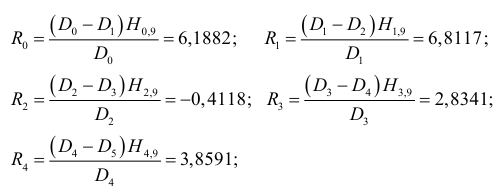
При нормальном распределении с вероятностью ошибки 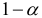, т. е. с уровнем доверия 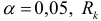. должно быть равно 1,96. Анализируя значения 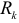, можно предположить, что путем образования разностей второго порядка более или менее исключена систематическая компонента исследуемого динамического ряда. В качестве оценки неизвестного рассеяния случайной компоненты возьмем 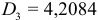, так как .

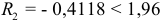Метод конечных (последовательных) разностей прост в реализации, но применять его следует осторожно, так как последовательные значения не являются независимыми и часто убывают (или возрастают), т. е. не сходятся к постоянному значению. Кроме того, сходимость не доказывает, что ряд первоначально состоял из полинома и случайной компоненты. Сходимость лишь подтверждает, что динамический ряд может быть приближенно представлен в виде полинома плюс случайная компонента. Тем не менее этот метод ценен тем, что дает верхний предел порядка полинома 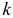, который целесообразно использовать для элиминирования тренда.

Авторсгрессионные модели

Анализируя динамические ряды, можно выявить, что при объяснении поведения переменной величины в течение некоторого периода используются значения той же величины в предыдущие периоды. Например, потребление в течение года изменяется не только в соответствии с наличными доходами в течение данного года, но также в зависимости от уровня потребления, уже достигнутого в предыдущем году. Поэтому модели, кроме текущих значений эндогенных переменных, часто содержат значения некоторых из этих переменных, которые они принимали в предыдущие периоды. Такие модели будем называть авторегрессиоными моделями. Они имеют следующий вид:

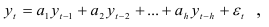
Число 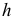определяющее количество периодов, от которых зависит текущее значение процесса 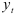, называется порядком авторегрессии. Если процесс 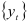может быть представлен в виде разностного уравнения

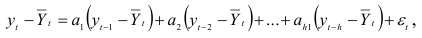
где 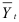— скользящая средняя динамического ряда, то он называется процессом скользящей средней.

Таким образом, модель авторегрессии является моделью стационарного процесса, выражающей значение уровня 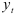динамического ряда в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей.

Авторегрессионое представление процесса особенно полезно для прогноза эволюции динамического ряда. Следовательно, авторегрессионые модели применяются, когда известно, что изучаемый процесс зависит от развития в прошлом. Авторегрессионые модели применяются также при определении преобразования, приводящего к процессу, близкому к последовательности независимых случайных величин. Речь идет о том, что, желая рассматривать случайный процесс, используют статистические методы, задуманные для применения к авторегрессионому представлению. Поэтому существуют методы формирования стационарных процессов из временных рядов. Рассмотрим их.

• Если уровни динамического ряда содержат линейный тренд

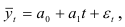
где 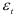— нормально распределенная случайная составляющая с нулевой средней и постоянной дисперсией, то разности первого порядка

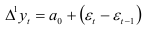
уже не содержат тренда. Поэтому 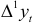— случайная величина, распределение которой полностью определяется распределением величины 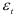Математическое ожидание разностей первого порядка 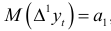так как 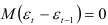, т.е. оно не зависит от 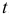. Если тренд динамического ряда характеризуется многочленом порядка 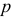и нормально распределенной случайной составляющей с нулевой средней и постоянной дисперсией 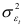: 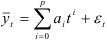, то разности прядка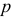

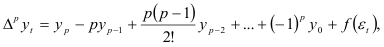
являясь случайной величиной с постоянным математическим ожиданием, также не зависят от 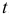. В этом случае .

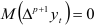Таким образом, динамический ряд, уровни которого характеризуются полиномиальным трендом и случайной компонентой с нормальным законом распределения 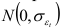, приводится к стационарному процессу образованием разностей, порядок которых определяется порядком полиномиального тренда.

• Пусть тренд динамического ряда представим в виде

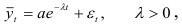
где 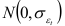— закон распределения случайной компоненты 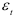. Тогда динамический ряд 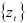, где 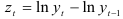, имеет постоянную среднюю — 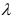, и может быть приведен к стационарному процессу.

• Рассмотрим аддитивную модель динамического ряда

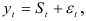
где 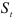— сезонная составляющая (постоянная пропорциональности, не меняющаяся от года к году); 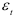— случайная компонента с законом распределения 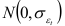, Тогда его уровни 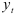колеблются около среднего значения с некоторым периодом 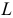, т.е. 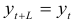, с точностью до случайной компоненты .

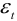Вычислим разности через 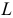шагов, т.е. 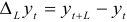. Случайная величина 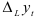, будет характеризоваться составляющей 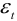. Следовательно, процесс 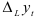— это стационарный процесс, среднее значение которого совпадает со средним значением исходного ряда.

Рассмотренные случаи сведения динамических рядов к стационарным процессам могут быть описаны с помощью символического оператора сдвига 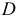, который преобразует 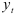в 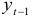, так что 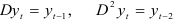и т.д.

Используя оператор сдвига, соотношение (7.8) можно записать так:

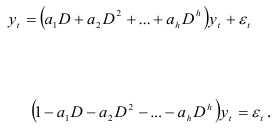
Определив оператор

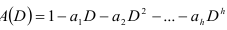
как полином степени 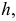получим уравнение в виде

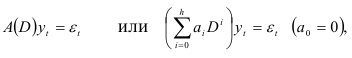
Уравнение (7.9) содержит 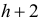неизвестных параметров: 1) 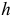коэффициентов 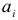среднее значение динамического ряда 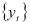; 3) дисперсию 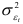случайной составляющей.

Можно показать, что уравнение (7.9) можно рассматривать как разностное неоднородное уравнение относительно 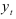. Для нахождения решения этого уравнения решим вначале соответствующее однородное разностное уравнение 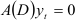. Его решение задается функцией

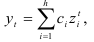
где 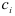— постоянные, определяемые из начальных условий; 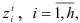-корни характеристического уравнения

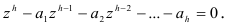
Уравнение (7.11) является уравнением степени 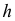и имеет ровно 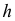корней. Предположим, что все корни уравнения (7.11) различны и 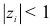для всех 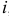, т.е. что все корни этого уравнения попадают внутрь круга единичного радиуса. Тогда с ростом 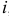решение (7.10) стремится к нулю.

Ряд (7.9) рассматривается как ряд, отражающий процесс, начавшийся далеко в прошлом. Тогда вклад решения (7.9) становится пренебрежимо мал и полное решение фактически совпадает с частным решением

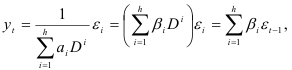
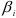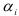где постоянные и определяются из тождества по :

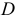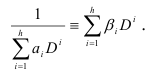
На практике корни уравнения (7.11) ищут редко. Тем не менее Уайз показал, что условия, налагаемые на эти корни, могут быть выражены в форме алгебраических связей постоянных .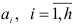

Если все корни уравнения (7.11) по модулю меньше единицы (условие устойчивости) и процесс 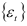стационарен, то процесс авторегрессии также стационарен.

Для построения авторегрессионых моделей необходимо:

1) исключить тренд и сезонную компоненту из динамических рядов;

2) проверить процесс на стационарность;

3) определить порядок модели авторегрессии;

4) оценить параметры авторегрессионой модели.

Эти действия могут повторяться в процессе уточнения модели, так как анализ авторегрессии не ограничивается построением только одной модели, а строится несколько моделей, после чего определяется порядок правильной модели.

Оценка параметров авторегрессионных моделей. Оценка параметров 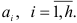авторегресспоной модели производится при следующих предположениях:

1) все корни характеристического уравнения (7.11) по модулю меньше единицы (условие устойчивости);

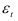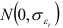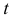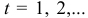2) случайная величина подчиняется нормальному закону распределения и не зависит от и , Значения 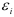и 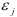статистически независимы при .

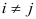Оценка параметров авторегрессионой модели осуществляется методом наименьших квадратов, методом максимального правдоподобия и методом коэффициентов автокорреляции.

Метод наименьших квадратов основывается на требовании минимизации остаточной дисперсии

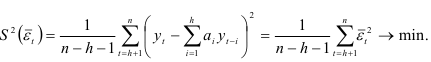
Применив процедуру метода, получим систему нормальных уравнений

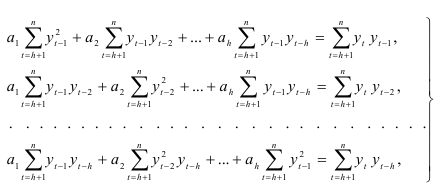
Корни системы (7.12) являются коэффициентами авторегрессии.

Метод коэффициентов автокорреляции предполагает построение системы уравнений с коэффициентами автокорреляции. Предположим, что процесс 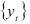имеет нулевое среднее значение, и умножим обе части равенства (7.8) на 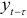. Будем иметь

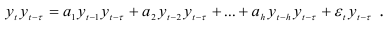
Просуммировав слагаемые уравнения (7.13) по 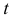, получим

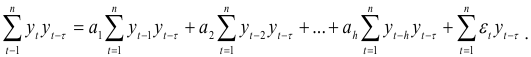
Так как 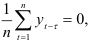, то 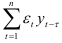является эмпирической ковариацией, а она равна нулю в силу статистической независимост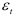и и 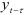. Умножив обе части равенства (7.14) на 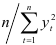заменим полученные суммы парных произведений

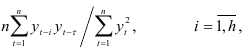
коэффициентами автокорреляций 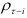, получим

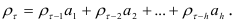
Уравнение (7.15) связывает коэффициенты автокорреляции процесса авторегрессии порядка 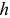. Подставляя в уравнение (7.15) значения 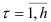и учитывая, что 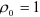и 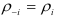, для любого 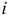, получаем систему уравнений Юла — Уокера для определения параметров 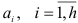, авторегрессионой модели:

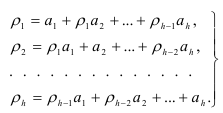
Решение системы (7.16) сводится к рекуррентным соотношениям:

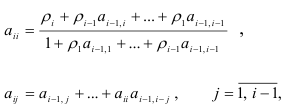
В качестве начального значения используется 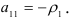Так как 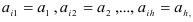то, применив формулы (7.17) и (7.18), получим оценки коэффициентов авторегрессионой модели порядка .

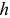Отметим, что, за исключением малых значений 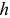, система (7.16) решается легче, чем система (7.12), так как ее матрица имеет более симметричную форму. В то же время при неограниченном увеличении числа наблюдений результаты оценок параметров 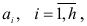по методу наименьших квадратов и с помощью коэффициентов автокорреляции совпадают.

Метод максимального правдоподобия состоит в построении функции правдоподобия и определении максимума этой функции. Координаты точки 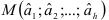являющейся точкой максимума функции правдоподобия, и будут оценками правдоподобия коэффициентов авторегрессионого процесса (7.8).

Проиллюстрируем определение оценок параметров авторегрессионых моделей первого и второго порядков.

Процесс авторегрессии первого порядка, называемый марковским процессом, описывается уравнением

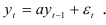
Из системы (7.16) следует, что единственный коэффициент модели (7.19) равен коэффициенту автокорреляции первого порядка 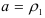Условие стандартности процесса авторегрессии первого порядка определяется неравенством 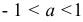. Итак, процесс (7.19) может быть записан в виде

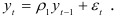
Процесс авторегрессии второго порядка, называемый авторегрессионым процессом Юла, описывается уравнением

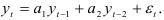
система (7.16) для случая 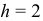имеет вид

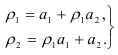
Решив ее методом Гаусса, получим:

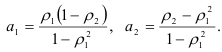
Для стационарности процесса авторегрессии второго порядка нужно, чтобы выполнялись неравенства

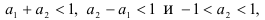
что следует из условия стационарности процесса.

Коэффициенты авторегрессии третьего порядка

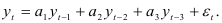
вычисляются по формулам:

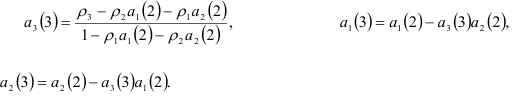
Так как с помощью рекуррентных формул мы находим оценки параметров регрессионных моделей, то их многократное использование при повышении порядка модели приводит к снижению точности описания исходного процесса. Поэтому повышение порядка модели при условии применения рекуррентных формул возможно лишь на 1-2 порядка. Дальнейшее повышение порядка модели авторегрессии должно сопровождаться решением системы (7.12) или (7.16).

Определение порядка авторегрессионых моделей. Одним из этапов построения авторегрессионой модели является определение ее порядка. Предварительная оценка порядка модели проводится на основе экономического анализа. Он позволяет выделять те уровни динамического ряда, которые оказали значительное влияние на его изменения в последующие периоды. Затем исследуется автокорреляционная функция

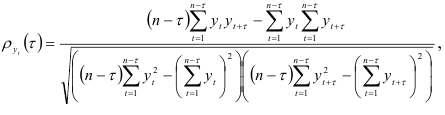
которая характеризует внутреннюю структуру динамического ряда. Функция (7.22) является нормированной, так как 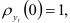и четной относительно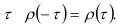

Так как автокорреляционная функция авторегриссионного процесса представляется в виде затухающих колебаний, то при ее анализе выясняют:

1) период колебаний, т.е. промежуток времени между двумя соседними максимальными значениями;

2) амплитуде/ колебаний;

3) фазу — угловую величину отклонения автокорреляционной функции от нулевого состояния (см. рис. 3.15, на котором приведен график автокорреляционной функции и указаны ее характеристики). По скорости затухания амплитуды можно сделать вывод о порядке модели авторегрессии.

Изменение автокорреляционной функции тесно связано со свойствами корней характеристического уравнения (7.11) и, следовательно, свойствами его коэффициентов. Если корни характеристического уравнения действительны, то автокорреляционная функция состоит из двух затухающих экспонент. Если больший по модулю корень положительный, то автокорреляционная функция убывает, оставаясь положительной. Если же больший по модулю корень отрицательный, то автокорреляционная функция убывает с изменением знака. Если корни комплексно-сопряженные, то автокорреляционная функция является затухающей с амплитудой 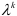, частотой 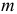и фазой 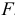, причем:

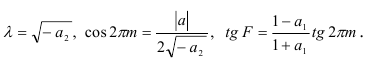
Далее исследуется частная автокорреляционная функция

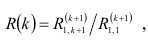
где 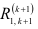— алгебраическое дополнение элемента первой строки и 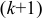-го столбца матрицы 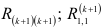— алгебраическое дополнение элемента первой строки и первого столбца матрицы 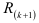. Матрица 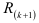состоит из коэффициентов автокорреляции динамического ряда:

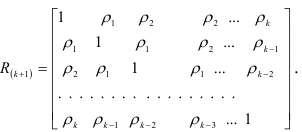
Элементы матрицы 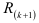— это коэффициенты автокорреляции разностного ряда 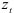с рядом, сдвинутым на 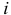временных промежутков 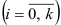. Значения частной автокорреляционной функции 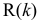для 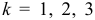могут быть выражены в явном виде через значения коэффициентов автокорреляции:

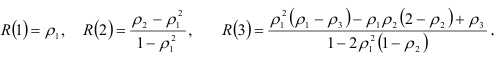
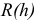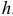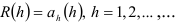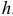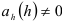Из формулы (7.23) и системы (7.16) следует, что значение частной автокорреляционной функции совпадает с коэффициентом при последнем члене авторегрессионой модели порядка , т.е. Отсюда получаем, что если исследуемый процесс является авторегрессионым порядком , то но 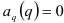для всех 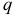>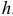. Используя этот признак, можно установить, описывается ли исследуемый процесс моделью авторегрессии порядка h или же требуется повысить порядок модели.

Отметим, что значения частной автокорреляционной функции при 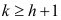имеют асимптотически нормальное распределение с нулевым математическим ожиданием и дисперсией 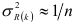, где 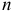— число уравнений динамического ряда.

Порядок авторегрессионой модели определяют, используя критерий Барлетта, состоящий в проверке гипотезы 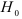о том, что исследуемый процесс представляет авторегрессию заданного порядка .

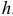Чтобы проверить гипотезу 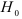, т.е. чтобы определить, достаточно ли высокая степень приближения получена в результате аппроксимации моделью (7.8) порядка 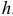, вычисляют отклонения, возникающие при повышении порядка авторегрессии. Для этого строят авторегрессионые модели порядка 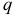, где 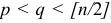, и находят суммы квадратов отклонений для тех уровней, для которых величину 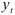можно вычислить с помощью модели как порядка 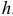, так и порядка 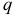. Тогда величина

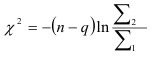
имеет распределение 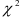с 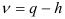степенями свободы. В формуле (7.24) 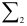сумма квадратов остатков для модели порядка 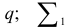— сумма квадратов остатков для модели порядка 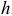, причем рассматриваются остатки, для которых определена модель порядка 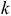. Если при уровне доверия 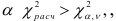то модель порядка 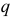даст существенно лучшую аппроксимацию остатков 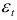по сравнению с моделью порядка 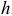. В противном случае, т.е. при 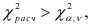гипотеза 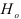о том, что авторегрессионая модель порядка 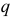даст лучшие результаты, отвергается, следовательно, авторегрессионая модель порядка 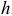является лучшей.

Рассмотренный критерий Барлетта является асимптотическим, поэтому для небольших выборок, содержащих менее 20 наблюдений, вычисляется финальная ошибка прогноза (ФОП). Процедура определения порядка авторегрессионой модели состоит в переборе авторегрессий различных порядков и выборе той из них, для которой финальная ошибка прогнозирования минимальна, т.е.

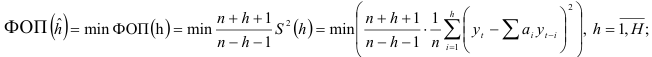
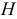— верхний предел порядка рассматриваемых моделей авторегрессии.

Построение авторегрессионых моделей для коротких динамических рядов. Динамические ряды экономических показателей предприятий и отраслей в основном содержат менее 20 наблюдений. Поэтому в оценке коэффициентов авторегрессий необходимо учитывать отклонения, возникающие вследствие несоответствия между объемом информации для данного динамического ряда и требуемой оценкой параметров модели. Продемонстрируем сказанное для авторегрессии первого порядка:

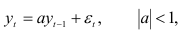
Метод наименьших квадратов приводит к оценке

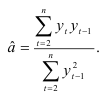
Л. Гурвиц изучил распределение 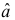и показал существование систематической ошибки в малых выборках. Когда процесс 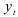рассматривается как стационарный и начальное значение 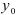— как случайное, когда 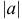мало, а 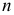велико, тогда математическое ожидание оценки а определяется формулой

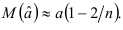
При неограниченном возрастании 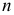систематическая ошибка 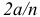бесконечно мала относительно средней квадратичной ошибки, равной 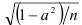. Для динамических рядов, содержащих около 20 уровней, она достигает примерно 10 % истинной величины.

Чтобы хорошо оценить свойства обычных методов (например, метода наименьших квадратов), когда аналитический подход затруднителен, приходится прибегать к изучению экспериментальных результатов. Исходя из известной авторегрессионой модели, достаточно сформировать некоторое число искусственных динамических рядов с одними и темы же вероятностными характеристиками и найти оценки для каждого из них, предполагая, что в действительности мы имеем дело лишь с различными реализациями одного динамического ряда. Тогда для каждой оценки мы будем располагать столькими значениями, сколько имеется динамических рядов. Эмпирическое распределение этих значений дает приближение к теоретическому закону, который мы хотели установить. Этот метод называется методом Монте — Карло, он был применен для изучения распределения оценки .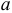

Изучение искусственных динамических рядов допускает также оценку статистических методов, связанных с методом наименьших квадратов. Асимптотическая теория обосновывает применение обычных формул для вычисления дисперсий оценок и установления критериев и доверительных интервалов. Но эти формулы применимы строго лишь для больших выборок. Поэтому важно установить, ведут ли они к заметным ошибкам для выборок, которые обычно изучаются в эконометрии. Установлено, что для малых выборок 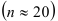дисперсия 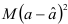дает в среднем достаточно точную оценку дисперсии 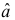. Этот вывод говорит о том, что применение методов обычной регрессии к авторегрессионым моделям не влечет за собой серьезной ошибки, если ошибки 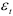неавтокоррелированы.

Некоторые другие методы построения авторегрессионых моделей. Оценивать параметры авторегрессионой модели, как отмечалось выше, можно методом наименьших квадратов. Точность модели повышается, если коэффициенты определены на основе минимизации выражения

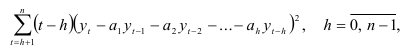
в котором уровням динамического ряда придают веса, причем больший вес соответствует последним наблюдениям, в наибольшей мере влияющим на последующие значения показателя.

Коэффициенты авторегрессионой модели можно находить путем минимизации коэффициентов автокорреляции случайных величин 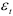, т.е. минимизируя функцию

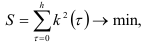
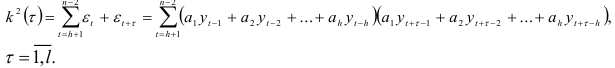
Приравнивая нулю частные производные по каждому коэффициенту 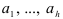функции 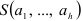получаем систему уравнений второй степени, которая даже при небольшом числе неизвестных решается со значительными трудностями.

Построение авторегрессионых моделей можно осуществить с помощью робастных методов. Робастной оценкой считается такая оценка, статистические свойства которой остаются достаточно хорошими при несоответствии наблюдений динамического ряда некоторым теоретическим предположениям. Согласно такому подходу, коэффициенты авторегрессионой модели определяют, минимизируя выражение

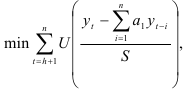
где 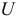— общая функция потерь. Эта функция вводится вследствие отклонения уровней динамического ряда от теоретических значений. Параметр 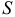вводится для масштабирования этих отклонений. Если параметры авторегрессионой модели определяются по методу наименьших квадратов, то 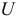— квадратичная функция.

Дифференцируя выражение (7.25) по параметрам 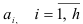, получаем систему нелинейных уравнений

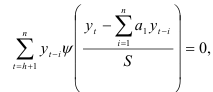
где 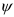— производная функции потерь.

Параметр масштабирования определяется из уравнения

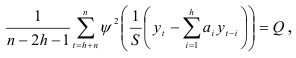
где 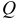— константа, которой придаются различные значения в зависимости от вида функции потерь. Решение системы (7.26) осуществляется методом последовательных приближений.

Авторегрессионые модели строят также методом адаптивной фильтрации. Суть его состоит в непрерывном пошаговом уточнении параметров модели, т.е. в поиске такого набора весов для корректировки параметров, который бы минимизировал квадрат ошибки прогноза. Поэтому авторегрессионую модель представляют в виде

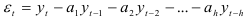
и параметры для начального приближения определяют, решая систему Юла-Уокера (7.16). Корректировку параметров в модели (7.27) осуществляют методом наискорейшего спуска, который определяет величину шага вдоль градиента в сторону убывания минимизируемой функции — квадрата ошибки прогноза, т.е. вдоль

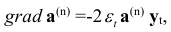
Где 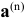— вектор коэффициентов модели (7.27); 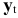— вектор уровней динамического ряда. Шаг в сторону убывания квадрата ошибки прогноза состоит в измерении вектора 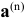по формуле

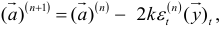
где индекс 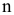показывает итерацию, для которой имеются прогнозируемое и фактическое значения показателя. Следовательно, может быть определена ошибк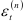а , а 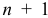— следующая итерация. Величина 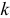— вес, с которым учитывается поправка к вектору коэффициентов метода. Теоретически необходимое и достаточное условие сходимости метода наискорейшего спуска — это условие 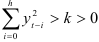, которое является слишком общим.

Поэтому чрезмерное увеличение 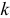может привести к тому, что какое-либо из значений весов пересечет свой минимум и вынуждено будет к нему возвращаться. А это способствует увеличению ошибки при недостаточном числе итераций. Из практического применения этого метода следует, что для каждого значения 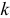существует оптимальное число итераций, и наоборот. Это значит, что величина 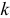тесно связана с числом уровней динамического ряда и числом итераций.

Пример 7.7.

Рассмотрим динамический ряд, характеризующий поквартальный объем продаж фирмы с 1980 по 1990 г. Данные, из которых исключена сезонная компонента, приведены в табл. 7.10.

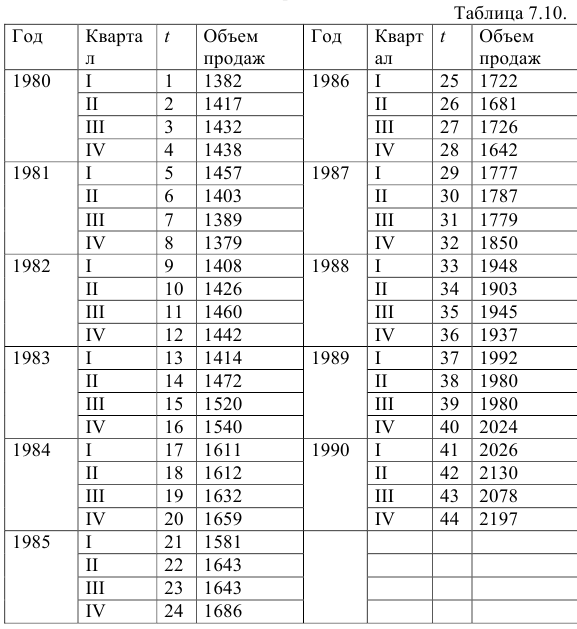
Построим авторегрессионую модель. На первом этапе определим ее порядок. Из исходных данных следует, что нужно рассмотреть авторегрессию 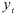на 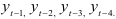. Для проверки этого вывода вычислим автокорреляционную функцию (7.22):

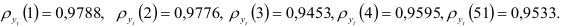
Значения автокорреляционной функции сначала затухают: 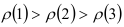затем возрастают: 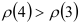снова начинают убывать: 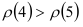. Следовательно, автокорреляционная функция состоит из двух затухающих экспонент.

Порядок авторегрессионой модели попытаемся определить, используя критерий Барлетта. Для этого построим авторегрессионые модели первого, второго, третьего и четвертого порядков и рассмотрим, как изменяются суммы квадратов отклонений для этих моделей. Параметры авторегрессионой модели четвертого порядка определим из системы Юла-Уокера (7.16):

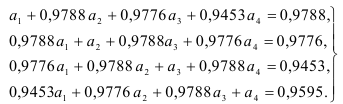
Решая систему, находим

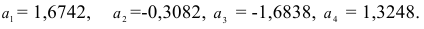
Следовательно, авторегрессионая модель четвертого порядка имеет вид

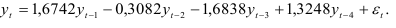
Коэффициенты авторегрессии второго порядка вычислим по формулам:

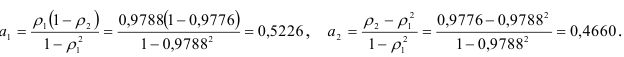
Тогда авторегрессионая модель второго порядка запишется уравнением

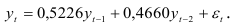
Коэффициенты авторегрессии третьего порядка определим из рекуррентных формул:

подставив которые в равенство (7.21), получим

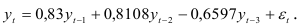
Марковский процесс авторегрессии первого порядка, как следует из равенства (3.89), имеет вид

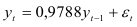
Вычислим далее для всех моделей суммы квадратов отклонений 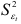тех уровней, для которых 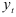можно вычислять с помощью модели четвертого порядка. Первое значение будет соответствовать первому кварталу 1981 г.

Сравнение моделей для простоты проведем для уровней 1990 г. (хотя нужно учитывать все уровни). Результаты приведены в табл. 7.11.

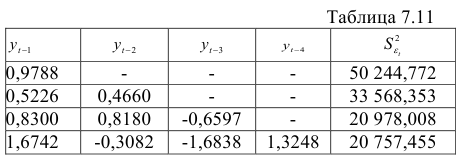
Суммы квадратов отклонений значительно уменьшаются при добавлении 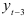. Поэтому сравним авторегрессионые модели третьего и четвертого порядков. Вычислим:

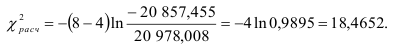
Квантиль 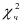распределения для уровня значимост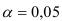и и 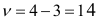степени свободы равен 3,841. Следовательно, 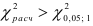что означает, что авторегрессионая модель четвертого порядка даст лучшую аппроксимацию остатков 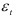чем модель третьего порядка.

Таким образом, продемонстрирован процесс построения авторегрессионых моделей.

Эта лекция взята со страницы предмета «Эконометрика»

Предмет эконометрика: полный курс лекций

Эти страницы возможно вам будут полезны:

Выбор функции тренда

Методы определения сезонных колебаний

Моделирование связных рядов динамики

Прогнозирование с помощью временных рядов