Оглавление:









Аналитическое решение для быстрых необратимых реакций
- В литературе по массообмену существует множество аналитических решений проблемы одновременной диффузии и химических реакций. Подход к этим решениям был изложен в предыдущей главе, посвященной Массоперенос.1. один из подходов основан на теории кино. Согласно этой теории, сопротивление массопереносу считается сосредоточенным в тонкой неподвижной пленке. Содержание Растворенного вещества мала. Другой подход заключается в рассмотрении процесса массопереноса как нестационарной диффузии в периодически возникающем обновленном жидком элементе. В интерфейсе. В качестве 3-го подхода рассмотрим расчет химических реакций на ламинарной границе.
Решение различных типов реакций известно, но рассмотрим только следующие очень быстрые и осуществимые необратимые реакции. А + Б = + АБ. Компонент а представляет собой диффузионное вещество, которое поглощается жидкостью из газа. Жидкая фаза содержит Нелетучий реагент в, который растворен в нелетучем абсорбенте С. Он также применим при массопереносе из жидкой фазы в газ с реакцией в газовой фазе, и когда происходит 2 массопереноса. Жидкость. Поскольку реакция протекает очень быстро и до конца, молекулы а и в существуют отдельно в любой плоскости, перпендикулярной направлению диффузии、 Невозможно.
Теплообмен конвекцией имеет место на внешних поверхностях бруска, при этом коэффициент теплообмена си может быть повсюду постоянным или равным на противоположных сторонах. Людмила Фирмаль
Когда диффузионный процесс в пленке жидкости достигает стационарного состояния, реагент а, имеющий постоянную концентрацию pL₈ на границе раздела пар-жидкость, проникает Концентрация па равна нулю в жидкой пленке до плоскости, где будет происходить реакция proceed. At в то же время концентрация потока жидкости равна B0.、 Реакция протекает, и пленка движется в противоположном направлении к плоскости, где концентрация pv также равна нулю. Это показано на рисунке. 43.1. Положение плоскости, в которой протекает реакция, зависит от концентрации pDa и pBo, а также от относительной скорости диффузии компонентов A и B.
Если коэффициент диффузии Vls чистого компонента B или жидкофазного компонента A очень мал, то реакция происходит на границе раздела газ-жидкость между компонентами A Она становится жидкой фазой только в составе соединения АВ. С другой стороны, если средняя концентрация компонента в в жидкой фазе очень мала, или если коэффициент диффузии L » если весь компонент B в жидкости очень мал, то плоскость, в которой будет протекать реакция, значительно сдвинется. Расстояние до глубины жидкости.
Наконец, если реакция не прогрессирует с высокой скоростью или не достигает конца, то вместо плоскости реакции имеется конечная зона реакции Толщина, при которой компоненты а и в становятся конечной концентрацией След. Диффузионный поток компонента а вблизи границы Устойчивые состояния равны Раздел (43.1) Жидкая фаза не возникает, и присутствие соединения AB не влияет на скорость диффузии компонента A. аналогичное предположение сделано в отношении диффузионного потока компонента B. (43.2) Так как количество молей компонентов А и в, входящих в реакцию, одинаково, то поток и-АВ в установившемся состоянии равны.
Заменить формулу (43.2) bv на 6t-6L. Объединив эту формулу с формулой (43.1), можно решить для толщины зоны, содержащей компонент A. с.—°ас-⁸a ..• лсСл » + ° вссво Подставляя эту формулу в Формулу (43.1), получим диффузный поток компонента А. (43.5) Сопоставьте формулу с формулой для коэффициентов Скорость массопереноса жидкой фазы этой системы ^ г = * ’(eA₈-0) дает следующее выражение для K $- Ч. Как показано в материале коэффициент передачи k₀ в отсутствие химической реакции. 33 на основе теории пленок,■в результате воздействия химических реакций на массоперенос Оно может быть выражено по отношению к » чему?».
Низкий коэффициент плотности потока p 27 диффузия уменьшает преимущества химических реакций и приближает процесс к чисто физическому поглощению. С другой стороны, более высокие значения этих величин являются、 Большое значение коэффициента массопереноса k’. Формула (43. 7) является результатом чрезмерного упрощения модели. Тем не менее, эта модель явно качественно корректна и отражает влияние химических реакций в простой форме. Но… Уравнение (43. 7) коэффициент массопереноса зависит от 2 концентраций: dDv irBo, и при расчете абсорбционной колонки необходимо знать эти значения каждого поперечного сечения. K’, чтобы решить.
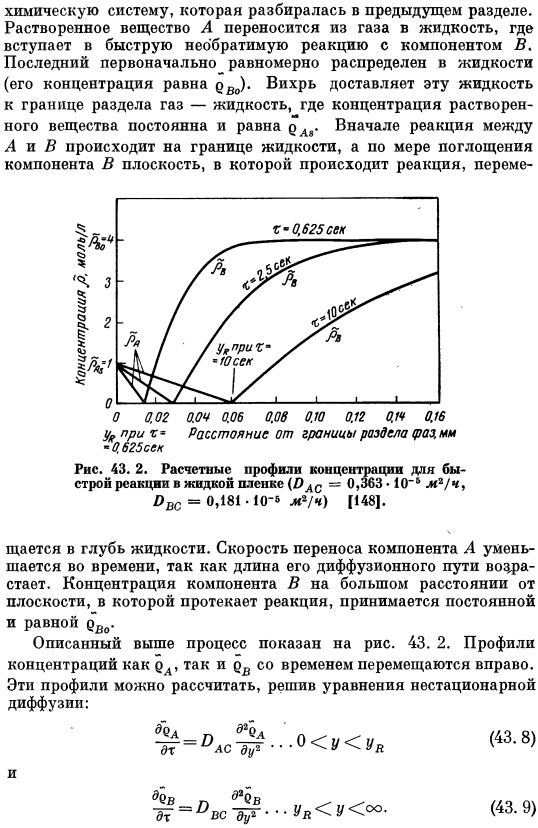
- Концентрация на интерфейсе pAa, с другой стороны, является Ch. As мы видели, что это зависит от соотношения коэффициента массопереноса двух фаз. 33.И так оно и есть. Для определения тяги массопереноса в каждом поперечном сечении колонны необходим метод ее решения с использованием метода последовательного приближения. ТС и я. Теория осмоса. 35 также служит основой для модели расчета массопереноса при химических реакциях[33, 1481. Химическая система описана в предыдущем разделе. Растворенный материал а переходит из газа в жидкость, где происходит быстрая необратимая реакция с компонентом В.
Последний, в первую очередь, равномерно распределяется по жидкости(его концентрация равна ео).Вихрь доставляет эту жидкость. К границе раздела газ-жидкость, где концентрация растворенного вещества постоянна и равна pAe. Первый、 Войдите в глубину liquid. As длина диффузионного пути увеличивается, скорость движения компонента а уменьшается со временем. Концентрация компонента B далеко от Предполагается, что плоскость, на которой будет протекать реакция, постоянна и равна pBo.
Метод для двухмерных задач может быть легко использован при решении трехмерной задачи и заключается в следующем. Людмила Фирмаль
Вышеописанный процесс показан на рисунке. 43. 2.Как pA, так и профили плотности цвета перемещаются вправо с течением времени. Эти профили могут быть вычислены путем решения нестационарного уравнения. Диффузия: ■ ■ ■ 0 Я. (43.8) Граничные условия жидкой фазы следующие: ёЛ =atatу= 0; эВ = эВ PR Т =°; — °Во ^» Пу г = гг- Эта задача аналогична обычной задаче нестационарной диффузии и лежит в основе теории осмоса Sec. 35.Но в этом вопросе есть дополнительная переменная UVs. Расстояние от границы раздела газ-жидкость до плоскости, в которой происходит реакция в любой момент времени. Дифференциальные уравнения (43. 8) и (43. 9) при совместном решении уравнения 35.
Частный случай 2EVS = решение OSA Существует относительно форма 0л» + ’ 0С. 2а°ЛСТ Мгновенный массовый расход при поглощении (43.10)) (43.11) Уравнение (43. 11) согласно уравнению (43. 10) при дифференцировании、 (43.12) Средний массовый расход при поглощении при контакте с поверхностью те равен (43.13) Формула (43. 12) и интегральное уравнение (43. 13) замена на: ^ л = 2(0А,+ ев «) Формула для определения среднего массового расхода через коэффициент массопереноса cd — (43. 5) и можно сравнить. Уравнение (43. 14) и (43. 5) уравнение дает следующее уравнение для k’. (43.15)) Эта формула называется формулой(35. 35) по сравнению с формулой 35.
Представляет собой коэффициент массопереноса чистого физического поглощения, основанный на теории осмоса. Соотношение: (43.16)) Поэтому в частном случае 2) А₀= OVS теория кино и теория осмоса дают одинаковые результаты. Если коэффициенты диффузии не равны, то соотношение〜 На основе теории осмоса она не равна соотношению, полученному с помощью теории пленок, а усложняется. Подробное решение этой проблемы было найдено в Шервуде и Пигфорд[148]. Химические реакции в ламинарных пограничных слоях. Последние исследования Фридлендера и Лиета [49]дают аналитическое решение проблемы диффузии и включают быстрые химические вещества. Реакция в ламинарном пограничном слое на плоской пластине.
Их решение ограничено случаями, когда скорость массопереноса мала, а обычными составляющими скорости на пластине являются Это было так ignored. In в этом случае профиль скорости пограничного слоя описывается решением Блазиуса, которое рассматривается в разделе 2. 12. Модель распространения практически идентична описанной в предыдущем разделе. Компонент а растворяет растворимые вещества или появляется на поверхности пластины、 Питание через поры плиты. Концентрация компонента а в жидкости на поверхности пластины постоянна и равна па>.Компонент B равномерно распределяется в свободном потоке、 он имеет концентрацию pBO и диффундирует через пограничный слой концентрации к плите.
Реагент расположен в нескольких плоскостях в пограничном слое. Реакция будет происходить. Реакция последовала незамедлительно. Когда он достигнет конца, концентрация обоих компонентов в этой плоскости будет равна нулю. Упрощенной формой дифференциального уравнения, описывающего диффузию в пограничном слое между пластиной и плоскостью, на которой протекает реакция, является: «Х DX » Последнее уравнение — t| = / | / «-^-и / (μ)=уменьшить концентрацию до безразмерной формы, а затем дифференцировать Уравнение (43.17) принимает вид: (43.17) (43.18) PDE, аналогичное уравнению (43.17), может описывать компонент B области между плоскостями, в которой происходит реакция.
Край концентрационного пограничного слоя. Формула (43. 18) Если вы хотите выполнить то же преобразование, которое привело к: — (с) Уравнение (43. 18) и граничные условия (43.19) являются: Формула (43. 18) и (43. 19) решается относительно u и ev, а уравнение массового расхода 43.
Определяется градиентом концентрации y = 0.Встань на этот путь Вы можете сравнить уравнение массового расхода с уравнением (43.5), чтобы получить уравнение k».Если умножить последнее на q—, то образуется локальное число Шервуда, которое будет: Связь между безразмерными группами: (43.20 )) Это локальное число Шервуда равно множителю* ——— Рассмотрим влияние химических реакций на системы, где чисто физическое поглощение occurs. In в некоторых случаях, как показано, 8sL = 8si; ————- 4 —-、то есть, фактор СКБ 9а Он идентичен поправочному коэффициенту, найденному на основе теории пленки и теории передачи.
В пределах предела 2vo 1 9vo (sy\ Если-больше, то коэффициент——— = я =- 9А, » — ^ ЛН е.\ & С8 / В среднем случае коэффициенты, учитывающие эффекты химических реакций, могут быть рассчитаны с использованием методов, описанных в исходном материале. В более поздней статье из Akrivos 11 мы покажем, что факторы, которые Фридлендер и Литт ввели с учетом химической реакции, могут быть применены не только к пластине, но и к другим элементам Форма поверхности. Распределения для других геометрических фигур наиболее точны для чисел Шмида больше 1, но 8-секундный»= » 1 ″ также считается очень точным. Поттер [127]применил интегральный метод Калмана к задаче, описанной в этом разделе.
Смотрите также:
| Азеотропная и экстрактивная ректификация | Термические параметры |
| Массопередача, сопровождающаяся химической реакцией | Термическое уравнение состояния идеального газа |

