Аналитическое доказательство теоремы о сложении скоростей

Аналитическое доказательство теоремы о сложении скоростей

Рассмотрим движение материальной точки М в системе 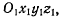совершающей некоторое движение относительно системы Oxyz (рис. 40). В каждый момент времени можно определить положение точки М как в системе 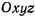так и в системе 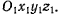Обозначим координаты точки 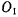в неподвижной системе координат через 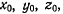координаты точки М в неподвижной системе координат через х, у, z, а координаты точки М в подвижной системе координат через 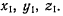Формулы преобразования дадут зависимость между координатами в неподвижной и подвижной системах

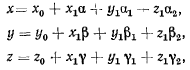
где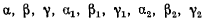

косинусы углов между соответствующими осями, определяемые из таблицы

Дифференцируя величины х, у, z, получим проекции абсолютной
скорости 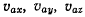на неподвижные оси координат. Из формул
преобразования будем иметь

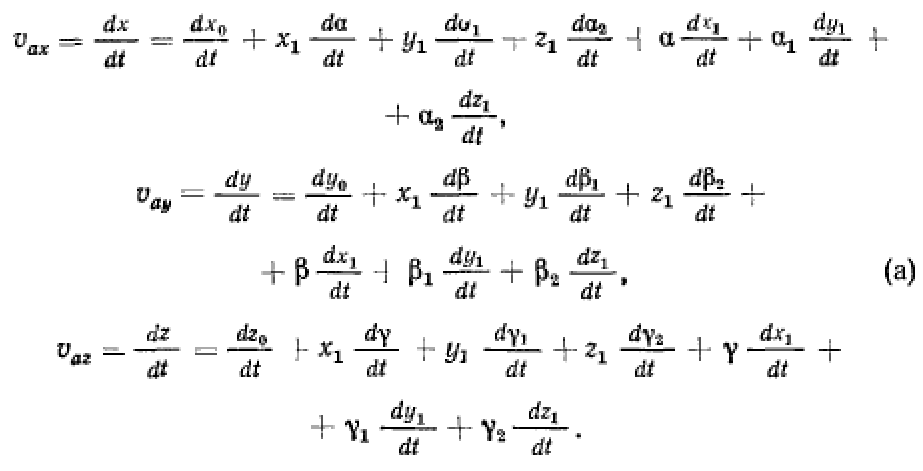
Для определения переносной скорости рассмотрим движение точки вместе с подвижной системой координат. В этом движении координаты 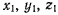остаются неизменными, а потому

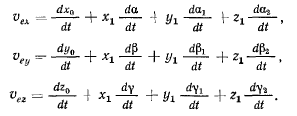
Положение точки относительно подвижной системы координат задается ее координатами 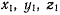поэтому проекции ее скорости в относительном движении на подвижные оси 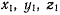будут равны
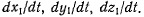Проекции же вектора относительной скорости на неподвижные оси координат найдем при помощи формул преобразования

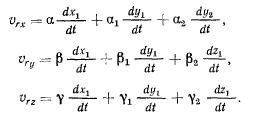
Сравнивая формулы (а), (b) и (с), получим выражения для проекций абсолютной скорости точки

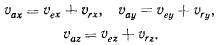
Откуда сразу же следует векторное равенство

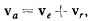
т. е. абсолютная скорость точки равна сумме ее переносной и относительной скоростей.

Сложение скоростей в общем случае сложного движения
точки. Рассмотрим сложное движение точки, движущейся относительно системы 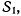которая, в свою очередь, совершает некоторое движение относительно системы 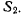Пусть, кроме того, система 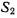совершает некоторое движение относительно системы 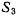и т. д. и, наконец, некоторая система 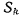совершает движение относительно системы S. Для определения скорости точки М относительно системы S воспользуемся теоремой о сложении скоростей. Обозначим скорость точки относительно системы 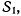через 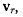, а через 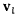— скорость относительно системы 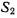той точки системы 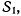с которой в данный момент совпадает точка М. По теореме о сложении скоростей находим скорость точки М относительно системы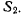

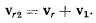
Обозначая далее через 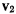скорость относительно системы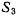
точки системы 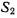с которой в данный момент совпадает точка М,
по теореме о сложении скоростей получим значение скорости
точки М относительно системы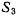

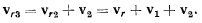
Продолжая процесс, определим значение скорости точки М относительно системы S

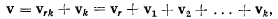
где 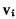— скорость относительно системы 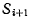точки системы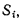
совпадающей в данный момент с точкой М.

Пример:

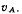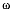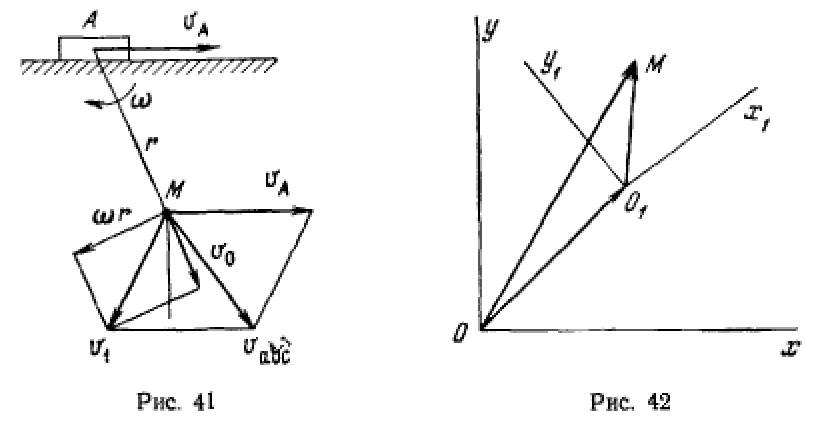
Ползун А скользит по прямолинейному рельсу со скоростью Вокруг точки А ползуна вращается со скоростью в вертикальной плоскости стержень АВ, по которому движется материальная точка М с относительной скоростью 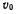(рис. 41). Определить абсолютную скорость точки М.

Решение:

Рассмотрим сначала систему, связанную со стержнем. Эта
система вращается относительно поступательно движущейся системы, связанной с ползуном. Переносная скорость точки М равна мг и направлена ортогонально к стержню. Складывая эту скорость 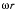скоростью 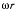получим скорость 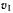движения точки М относительно системы, жестко связанной с ползуном. Для определения абсолютной скорости точки М сложим скорость 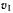со скоростью поступательного движения системы вместе с ползуном.

Замечания. 1. Положение точки М относительно неподвижной системы отсчета Оху можно определить радиус-вектором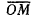
(рис. 42). Определяя положение начала подвижной системы
координат радиус-вектором 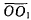и положение точки М в подвижной с
системе координат радиус-вектором 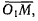составим векторное равенство

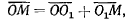
справедливое для любого момента времени. Дифференцируя это
соотношение, получим

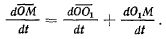
Здесь дифференцирование левой и правой частей равенства должно
быть выполнено в одной и той же системе координат, поэтому
производная 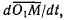рассматриваемая в неподвижной системе координат не будет совпадать с относительной скоростью точки так же, как и 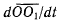не совпадает с переносной скоростью точки.

Относительное движение точки рассматривается относительно движущейся системы отсчета. Если же остановить подвижную систему, то изменится и характер относительного движения точки.

Пример:

Пусть подвижная система отсчета 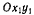вращается вокруг начала неподвижной системы с угловой скоростью (о. Определить относительную 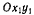скорость точки М, покоящуюся в неподвижной системе отсчета.

Решение:

Рассмотрим точку М, неподвижную относительно неподвижной системы отсчета. Для определенности будем предполагать, что точка М находится на неподвижной оси Ох. Тогда абсолютная скорость точки М равна нулю. Ее переносная скорость и скорость относительно подвижной системы координат по величине равны произведению 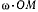и направлены в противоположные стороны. Если же остановить подвижную систему, то скорость точки М относительно этой покоящейся системы координат будет равна нулю и не будет равна относительной скорости по отношению к системе, движущейся относительно неподвижной.

Переносная скорость точки не зависит от характера относительного движения точки, но зависит от ее положения в подвижной системе отсчета и от движения подвижной системы координат.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Теорема о сложении скоростей в сложном движении точки

Метод Роберваля построения касательных к плоским кривым

Элементарные движения твердого тела

Скорость поступательного движения