Оглавление:






Аналитический расчет многопролетных статически определимых балок
- Аналитический расчет многошпиндельной статически определяемой балки аналитический расчет многошпиндельных шарнирных балок заключается в определении коэффициента внутренней силы от заданного удара. 309epure изгибающего момента и поперечной силы. В любом многопролетном шарнире балки опорного стержня всегда три и более. Эти опорные соотношения от внешних воздействий имеют ту опору, что уравнение статического равновесия не является хорошо известным и поэтому уравнение статического равновесия не существует в достаточной степени. Как известно, любой
цилиндрический шарнир, который можно вращать, можно противопоставить любому другому (или иначе, такое вращение возможно). Поэтому изгибающий момент шарнира равен нулю. По определению изгибающий момент в сечении любой системы, доказанный в ходе сопротивления материала, все расположен слева или справа от рассматриваемого сечения, то для каждого промежуточного шарнира балки составляется дополнительное уравнение из условия, что изгибающий момент от всех сил расположен слева или справа от рассматриваемого сечения.: 2M l e при 2A4p p=0. Тсс. Это уравнение является статическим
уравнением, так как оно записывается из состояния равновесия определенной Людмила Фирмаль
части системы. Такое дополнительное уравнение может быть записано в том же числе, что и промежуточное соединение в балке. Необходимое количество промежуточных соединений в балке определено выше и равно W=S0P-3. Таким образом, система из трех уравнений статического равновесия наряду с дополнительным уравнением 2l1lev=2L1^p=0, полная система уравнений разрешения, в которой определяются все опорные реакции многошарнирного пучка, является системой уравнений статического равновесия, поэтому вычисленные пучки могут быть определены статически. Расчет многопролетной совместной балки с использованием полной системы уравнений разрешения не всегда оправдан, но он решает систему одновременных уравнений со многими неизвестными в
реальных расчетах, полная система уравнений может быть разделена на ряд подсистем, каждая из которых содержит.- 310x j [t часть неизвестного. Разделение на подсистемы осуществляется на основе анализа взаимодействия отдельных элементов многопролетной шарнирной балки. Характер передачи силового взаимодействия от одного элемента к другому отражен в схеме балочного перекрытия. Таким образом, схема перекрытия балки указывает порядок ее расчета. Расчет начинается с верхнего вторичного луча, за которым следует переход к нижнему вторичному лучу и главному лучу. Верхняя вторичная балка рассчитывается на основе нагрузки,
- приложенной непосредственно к этим балкам. Нижележащие вторичные и главные балки рассчитываются с учетом нагрузки, которая непосредственно приложена к этим балкам, и опорного давления, которое передается от соседних верхних вторичных балок. Опорное давление равно опорной реакции луча, который находится сверху, но имеет противоположное направление. Конечная эпюра изгибающего момента и поперечной силы многопролетной шарнирной балки представляет собой сумму соответствующих эпюр отдельных элементов. М и Q при строительстве участка соблюдают те же правила знаков, которые используются в процессе сопротивления материала. Изгибающий момент считается положительным, если в рассматриваемом поперечном сечении балка изогнута вниз выпуклой формой (волокна дна растянуты). Если его направление
совпадает с вращением остальной части луча по часовой стрелке, то боковая сила считается положительной. Участок M на вертикальной оси откладывается со стороны растянутого волокна балки,а положительный участок y-Q откладывается от его оси. Детали расчета объясняются на примере. Например. Для многошпиндельных шарнирных балочных участков M и Q(рис. 28.3, а). Решение. Во-первых, давайте сделаем кинематический анализ. В этой колонке D=4, W=3 и SOP=6. Степени свободы 1^^3 » 4-2-3-6=0. Балка имеет необходимое количество соединений. Перейдем к анализу геометрических структур. Пара балок крепится к Земле на b, поддерживаемый жесткой муфтой. Этот неподвижный диск (Земля), два стержня в шарнире C, диск CDE установлен опорным стержнем в точке D. полученная система из двух дисков BC и CDE
неизменна и неподвижна. Балка eqh крепится к Земле двумя вертикальными Людмила Фирмаль
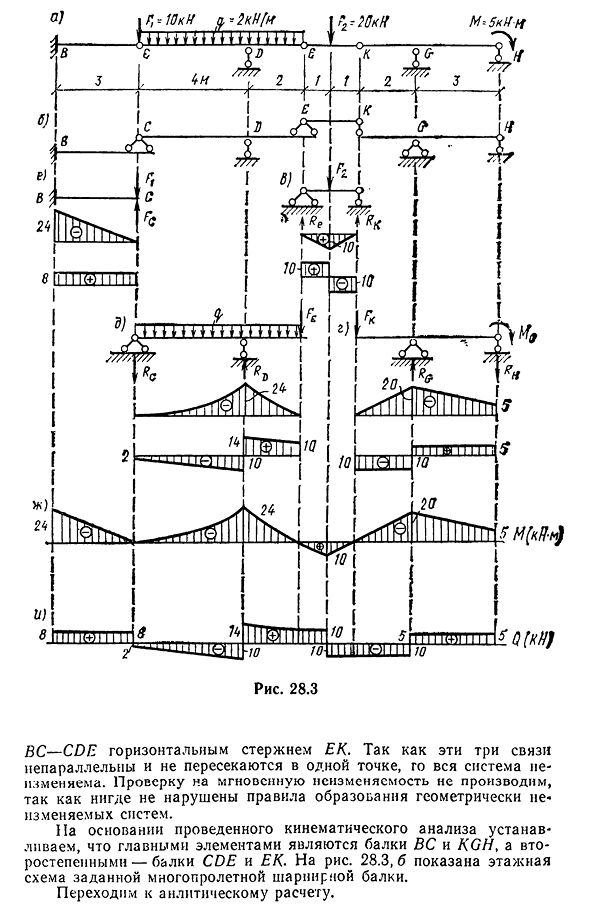
опорными стержнями, g и//, и крепится к системе крепления 311o/ д — °тонна—» М 5 I ле Г, С г с п- [ В) 1ngngn1n1£Ni[Внпниигф£G%. Я Два. 1кв [ I1 я, я, я … Я ф Один. 20р& ^shwpppp1 Десять. Пять. ) £4 ‘ GP^TGG» U) Восемь. Двадцать. ^thtt^P! b lK^rfT^I GPPTGTTT/m(Sch ГТ & ‘JAxtr Рис 28.3 До н. э. — турник ЕК по ЦДО. Поскольку эти три соединения непараллельны и не пересекаются в одной точке, вся система неизменна. Поскольку нигде не нарушаются правила формирования геометрически инвариантных систем, проверки на сиюминутную неизменность не производятся. На основе кинематического анализа было выяснено, что основными элементами являются балки BC и KGH, а двумерными элементами-балки CD и EC. Для риса. 28.3, b показана схема перекрытия данной многопролетной шарнирной балки. Переходим к аналитическому расчету. 312º давали пучок
начинается от верхней части второстепенной балки ЕК. Балка ЭЦ представляет собой однопролетную балку с шарнирной опорой, фокусирующей F2(рис. 28.3, б). Находим опорную реакцию Re и Rk по формуле:? SM£=F2-l-R k-2=0, RK=10kN; = re-2-F2-1=0,re=10kN. Для построения графиков M и Q рассчитываются изгибающий момент и боковая сила в характерном поперечном сечении балки EC. Раздел E. ME=Q\Qe=re = Q1 kN. Средняя часть пролета. МС^=РЕ’1=10кн-см;<2slrv= = ю кн;<е£ = ре-Ф2= — ю кн. Постройте графики M и q в соответствии с полученными данными. Второстепенной балки ЕЦ передает давление на главный идеальной отправной точкой для экскурсий балки и второстепенной балки ЦДО. Во-первых, рассчитайте дальний луч KGH, который является левой консолью и однопролетной балкой.
Балка нагружена собственным изгибающим моментом нагрузки. Для этой нагрузки, если опорное давление FK от балки выше приложено к точке K, опорное давление равно опорной реакции/+=/?К=10кн, а вниз направлены в обратном направлении (рис. 28.3, г). Мы находим реакцию поддержки из уравнения:10-2 + 5 + 7?h-3=0/?h=5kN; SMH=-10-5+ РГ-3+5=0рг=15кн. Для того, чтобы построить участок M и Q, изгибающего момента и поперечной силы в характерных сечения идеальной отправной точкой для экскурсий луча рассчитываются. Секция K. AfK=O; Qk= — FK=\0kN. Раздел G. П10= — ФК-2= — 20кн-м;м ФБ — ФС — — — — — СКН; QqP—Fk+Rg=5kN. Раздел Н. МН= — МО-5кн-м;Qх=РЗ=5кн. Согласно этим данным, мы строим эпюры м и Q. Теперь перейдем к расчету второго вторичного пучка CDE(рис. 28.3, г). CDE балка имеет
свою собственную равномерно распределенную силу нагрузки q=2кн / м. нагружена. Его опорное давление равно опорной реакции Re и направлено вниз, Le=10kN. Мы находим реакцию поддержки из уравнения: % MS=Fe-b+d-6-3 — РД-4=0,7?d=24kN; SMD=F= — 2-g-6-1 — /?C-4=0, Rc=2kN. Рассчитайте изгибающий момент и боковые силы в характерной части балки CDE. Секция C. MS=0′, Qc=R c= — 2kN. Раздел D. L4R= — 4—^-4-2 = -24 кН-м;<?ov= — Rc-q-i= — 10kN;<?Или= — I C-9-4 + /?Д=14кн. Секция E. ME=0; Q=FE=10kN. 313 участок М и q по этим данным. Наконец вычислите главный луч солнца(рис. 28.3, e), это консоль с жесткой опорой в сечении B. балка нагружена точками с собственной концентрацией F|. Опорное давление вторичного луча равно Fc=^2kN и передается вверх в ту же точку. Равнодействующие силы Fi и Fc направлены вниз, равны их разности F / — Fq^s kN. Для
консольных салазок можно рассчитать изгибающий момент и боковые силы характеристического сечения непосредственно от рабочей нагрузки, а не определять опорную реакцию. Раздел V. мя=-(М-ФК) -3= — 24kN-М;ку=Фи-ФК=8kN. Раздел C. L1C=0 » Qc=Ft-Fc=8kN. По этим данным строятся графики M и Q, а конечные графики M и Q в заданной многопролетной шарнирной балке составляют 28,3, W, и) отдельно для каждого элемента. Рассмотрим рациональное расположение промежуточных соединений многопролетных шарнирных балок для создания наиболее экономичной конструкции. С позиции минимального расхода материала средний шарнир
должен быть устроен так, чтобы максимальный изгибающий момент в пролетном строении был равен по абсолютной величине моменту на опоре, такие балки называются равноудаленными. Например, в балке, имеющей равные три пролета, нагруженной равномерно распределенными нагрузками,для создания импульсной структуры, равной промежуточному пролету на расстоянии 0,15/от опоры 28.4, а).
Смотрите также:
Решение задач по технической механике
| Мгновенная изменяемость системы | Трехшарнирные арки. Общие сведения |
| Виды многопролетных балок. Условия неизменяемости | Аналитический расчет трехшарнирной арки |
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

