Оглавление:
Аналитические условия равновесия произвольной пространственной системы сил. Случай параллельных сил
Как уже было установлено, для равновесия пространственной системы сил необходимо и достаточно, чтобы равнялись нулю главный вектор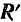 
и главный момент 
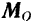этой системы относительно произвольно выбранного центра приведения.
Этим условиям можно придать и более удобную для практических целей аналитическую форму. Из формул (8) и (37) для модулей главного вектора и главного момента пространственной системы сил следует, что они обращаются в нуль при соблюдении следующих шести условий:
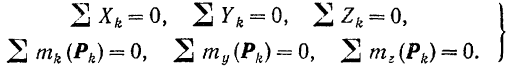
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из трех произвольно выбранных, но не лежащих в одной плоскости координатных осей, и суммы моментов всех сил относительно каждой из трех координатных осей.
Заметим, что при составлении уравнений моментов нет необходимости в том, чтобы оси, относительно которых берутся моменты сил, совпадали с осями проекций. Для простоты решения уравнений рекомендуется оси проекций располагать перпендикулярно к линии действия одной из неизвестных сил, вследствие чего проекции этой силы исключаются из соответствующего уравнения проекций. Ось моментов рекомендуется выбирать в плоскости одной из неизвестных сил. Тогда момент этой силы относительно данной оси будет равен нулю.
Одним словом, оси всегда нужно выбирать так, чтобы в каждое из шести уравнений равновесия вошло возможно меньшее число неизвестных.
Рассмотрим теперь частный случай — условия равновесия пространственной системы параллельных сил.
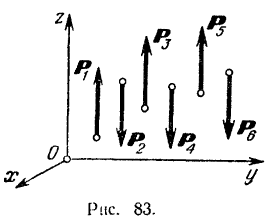
Пусть мы имеем систему параллельных сил
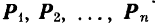
Так как выбор координатных осей произволен, то возьмем ось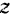 
параллельной данным силам и составим шесть уравнений равновесия произвольной пространственной системы сил. Так как оси 
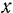и 
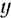перпендикулярны к данным параллельным силам, то проекции на эти оси каждой из сил системы будут равны .нулю. Следовательно, при таком выборе координатных осей уравнения
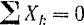
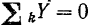
удовлетворяются независимо от того, находится ли система в равновесии или нет, а потому перестают быть условиями равновесия. Так как все данные силы параллельны оси г, то проекции их на эту ось равны модулям этих сил, взятым со знаком плюс или минус, в зависимости от того, в какую сторону они направлены. Следовательно, уравнение
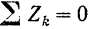
можно заменить уравнением
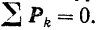
Отпадает также и условие
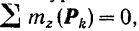
так как моменты всех сил относительно параллельной им оси 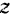будут всегда порознь равны нулю, при любом значении сил и любом их расстоянии от оси .
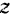Таким образом, для системы параллельных сил остаются только три уравнения равновесия
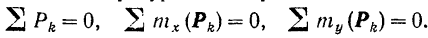
Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю алгебраическая сумма всех сил и сумма моментов всех сил относительно каждой из двух осей, лежащих в плоскости, перпендикулярной к данным параллельным силам.
Нужно сказать, что все выведенные ранее уравнения равновесия для частных случаев расположения сил можно было бы получить из шести уравнений (38) равновесия произвольной пространственной системы сил, подобно тому как это было сделано выше для пространственной системы параллельных сил.
Для каждого случая расположения сил достаточным является вполне определенное число условий равновесия, и потому для каждого из них можно написать только определенное число независимых уравнений равновесия. Это важно помнить, так как при числе неизвестных, превышающем то число независимых уравнений, которое возможно составить для данного случая расположения сил, задача становится статически неопределенной.
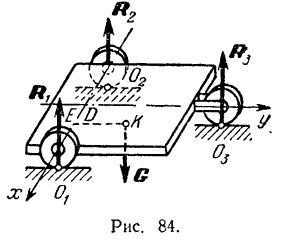
Пример задачи:
На платформе трехколесной тележки в точке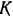 
лежит груз 
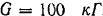. Найти давление каждого колеса тележки на пол, пренебрегая ее собственным весом, если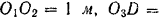 
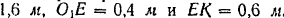. Точка 
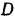лежит в середине отрезка 
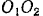(рис. 84).
Решение:
Тележка находится в равновесии под действием пространственной системы параллельных сил: веса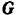 
груза и реакци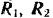и 
и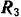 
пола. Имеем три неизвестных и возможно составить три независимых уравнения равновесия.
Возьмем в плоскости, перпендикулярной к линиям действия данных сил, ос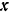и 
и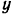 
так, как показано на рис. 84, и найдем моменты всех данных сил относительно этих осей:
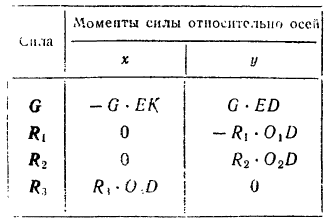
Уравнение равновесия имеют вид
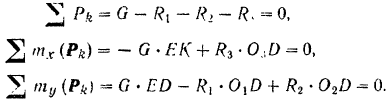
Решая систему уравнений и подставляя числовые данные, получим:
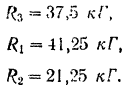
Искомые давления колес па пол, очевидно, равны по модулю найденным реакциям.
Пример задачи:
На валу трансмиссии насажены два шкива ременной передачи (рис. 85, а). Диаметры шкивов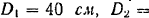 
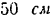от подшипника 
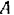эти шкивы находятся на расстоянии 
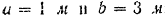; расстояние между подшипниками 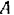и 
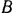равно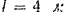 
. Ветви ремня, надетого на первый шкив, образуют с вертикалью угол 
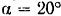; ветви ремня, надетого на второй шкив, горизонтальны. Даны натяжения 
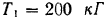и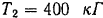 
ветвей первого ремня и натяжение 
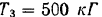верхней ветви второго ремня. Найти, при каком натяжении 
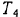нижней ветви второго ремня вал, находясь под действием приложенных к нему сил, будет в равновесии, а также определить реакции подшипников, вызываемые натяжением ремней.
Решение:
Так как все силы расположены в плоскостях, перпендикулярных к оси вала, то реакции подшипников не будут иметь составляющих, направленных вдоль оси вала (т. е. по оси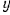 
). Составляюще
реакций подшипников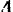 
и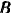 
по осям 
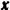и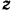 
обозначим соответственно через 
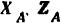и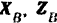 
. Для их определения спроектируем
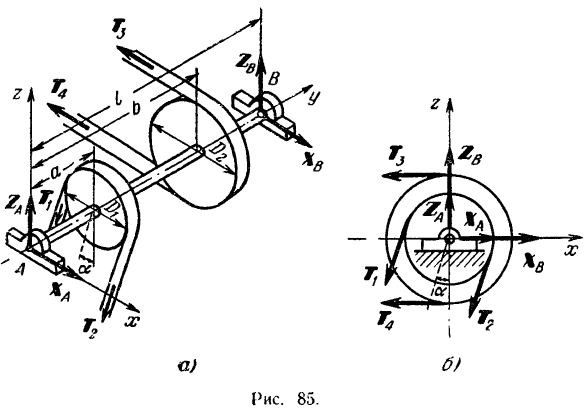
все силы приложенные к валу на ос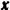и и 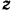и найдем моменты их относительно осе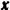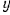й , и 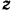(см. таблицу):
Составляя соответствующие уравнения равновесия, получим:
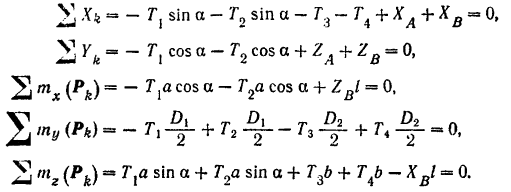
Решая эту систему уравнений и подставляя числовые данные, находим:
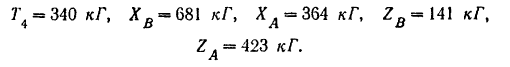
Пример задачи:
Прямоугольная дверь, вращающаяся около вертикально оси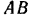 
открыта на угол 
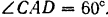Она
удерживается в этом положении грузом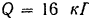 
, подвешенным на веревке 
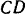, перекинутой через блок и концом 
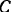прикрепленной к двери, и некоторой силой 
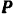, приложенной в точке 
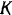двери и направленной перпендикулярно к ее плоскости. Вес двери 
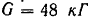, ее ширина 
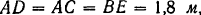, высота 
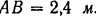. Определить модуль силы 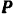, а также реакции шарнира в точке 
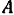и подпятника в точке 
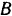, если 
.
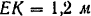Решение:
Дверь находится в равновесии под действием активных сил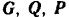 
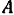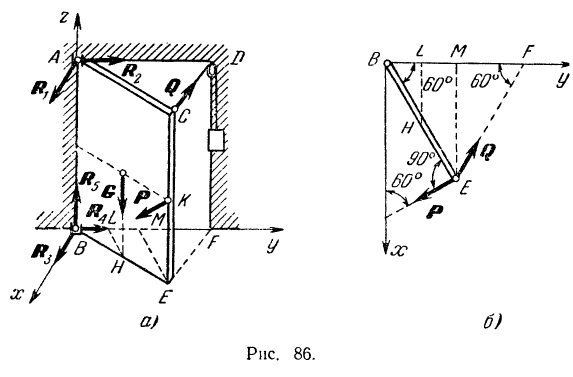
и реакций подшипника и подпятника 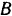. Проведем координатные оси, как показано на рис. 86, а, и разложим реакции связей на составляющие по этим осям. Так как цилиндрический шарнир 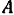допускает скольжение двери в вертикальном направлении, то его реакция не будет иметь вертикальной составляющей и разлагается лишь на две составляющие 
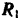и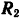 
. Реакция же подпятника 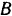дает составляющие 
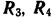и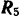 
, направленные по трем координатным осям. Расположение сил показано на рис. 86, а. Для удобства определения проекций и моментов сил 
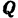и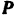 
, проекции их на плоскость 
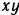показаны на рис. 86,6.
Составляем таблицу проекций всех сил на выбранные оси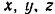 
и моментов сил относительно этих осей.
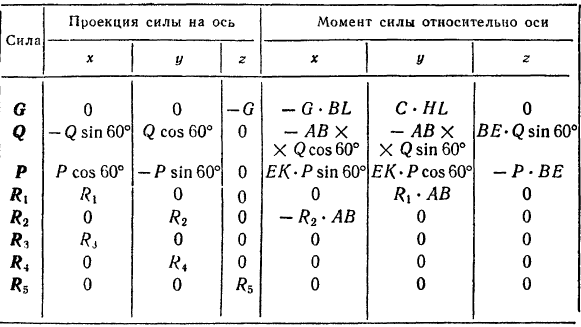
Уравнения равновесия принимают вид:
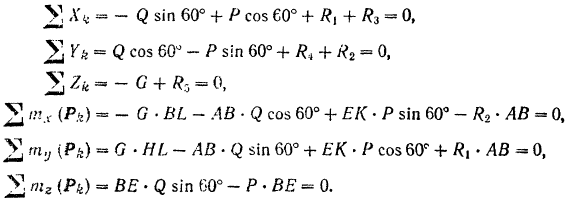
Из рис. 86,б находим:
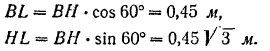
Подставляя в уравнения все данные и решая их, получим:
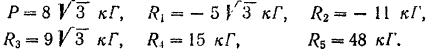
Отрицательные значения, полученные для 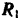и 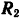, означают, что направления этих сил, указанные па рис. 86, надо изменить на противоположные.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
