Оглавление:
Для поиска асимптот можно использовать следующий алгоритм:
1. Для поиска вертикальных асимптот находим точки, не принадлежащие области определения (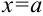 ) и проверяем следующее условие: если
) и проверяем следующее условие: если 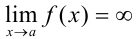 , то
, то 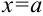 — вертикальная асимптота.
— вертикальная асимптота.
Вертикальных асимптот может быть одна, несколько или не быть совсем.
2. Для поиска горизонтальных асимптот находим 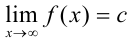 .
.
- Если
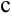 — число, то
— число, то 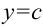 — горизонтальная асимптота;
— горизонтальная асимптота; - Если
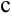 — бесконечность, то горизонтальных асимптот нет.
— бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим 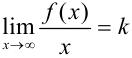 .
.
- Если
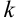 — число, отличное от 0, то находим
— число, отличное от 0, то находим 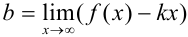 . Тогда
. Тогда 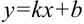 — наклонная асимптота;
— наклонная асимптота; - Если
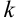 — бесконечность, то наклонных асимптот нет.
— бесконечность, то наклонных асимптот нет.
Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем — их нет. Рассмотрим примеры нахождения асимптот функции:
Пример №16.1.
Найдите асимптоты кривой 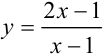 .
.
Решение:
1. Найдем область определения функции: 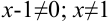 .
.
Проверим, является ли прямая 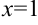 вертикальной асимптотой. Для этого вычислим предел функции
вертикальной асимптотой. Для этого вычислим предел функции 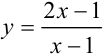 в точке
в точке 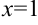 :
: 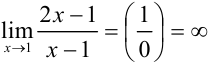 .
.
Получили, что 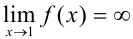 , следовательно,
, следовательно, 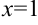 — вертикальная асимптота, х—>1
— вертикальная асимптота, х—>1
2. Для поиска горизонтальных асимптот находим 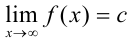 :
: 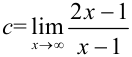 .
.
Поскольку в пределе фигурирует неопределенность 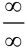 , воспользуемся правилом Лопиталя:
, воспользуемся правилом Лопиталя: 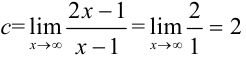 . Т.к.
. Т.к. 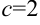 (число), то
(число), то 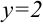 — горизонтальная асимптота.
— горизонтальная асимптота.
Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.
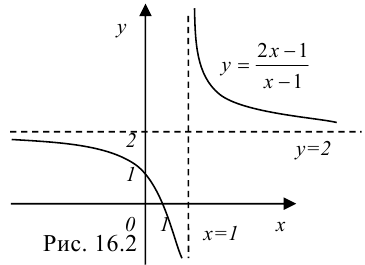
Таким образом, данная функция имеет вертикальную асимптоту 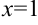 и горизонтальную асимптоту
и горизонтальную асимптоту 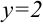 . Для наглядности график данной функции представлен на рис. 16.2.
. Для наглядности график данной функции представлен на рис. 16.2.
Пример №16.2.
Найдите асимптоты кривой 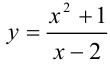 .
.
Решение:
1. Найдем область определения функции: 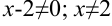 .
.
Проверим, является ли прямая 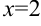 вертикальной асимптотой. Для этого вычислим предел функции
вертикальной асимптотой. Для этого вычислим предел функции 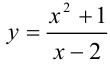 в точке
в точке 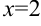 :
: 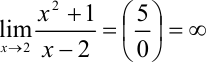 .
.
Получили, что 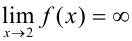 , следовательно,
, следовательно, 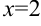 — вертикальная асимптота.
— вертикальная асимптота.
2. Для поиска горизонтальных асимптот находим 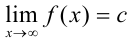 :
: 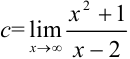 .
.
Поскольку в пределе фигурирует неопределенность 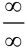 , воспользуемся правилом Лопиталя:
, воспользуемся правилом Лопиталя: 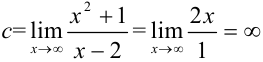 . Т.к.
. Т.к. 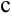 — бесконечность, то горизонтальных асимптот нет.
— бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим 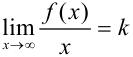 :
:
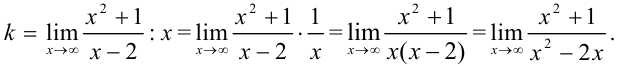
Получили неопределенность вида 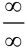 , воспользуемся правилом Лопиталя:
, воспользуемся правилом Лопиталя: 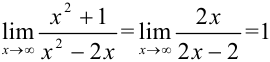 . Итак,
. Итак, 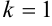 . Найдем
. Найдем 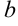 по формуле:
по формуле: 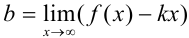 .
.
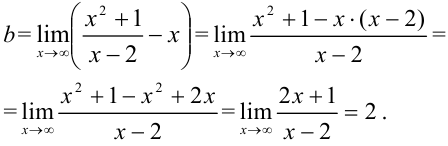
Получили, что 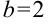 . Тогда
. Тогда 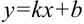 — наклонная асимптота. В нашем случае она имеет вид:
— наклонная асимптота. В нашем случае она имеет вид: 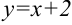 .
.
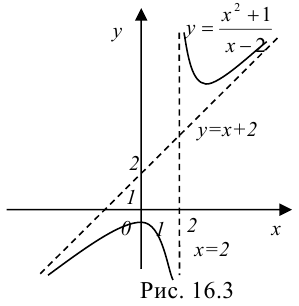
Таким образом, данная функция имеет вертикальную асимптоту 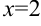 и наклонную асимптоту
и наклонную асимптоту 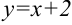 . Для наглядности график функции
. Для наглядности график функции 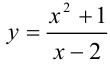 представлен на рис. 16.3.
представлен на рис. 16.3.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Критерий выпуклости-вогнутости функции и точек перегиба. |
| Понятие асимптот |
| Общая схема исследования функции и построения графика |
| Понятие неопределенного интеграла. |

