Алгоритм нахождения обратной матрицы

Для составления обратной матрицы используют следующую схему:

1. Вычисляют определитель матрицы , причем .
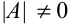2. Находят алгебраические дополнения элементов матрицы и составляют матрицу алгебраических дополнений :
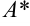3. Составляют матрицу 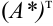, транспонируя матрицу .
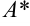4. Находят обратную матрицу по формуле:

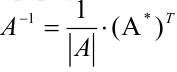
Пример №3.1.

Найдите матрицу, обратную матрице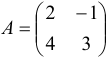

Решение:

1. Находим определитель матрицы :

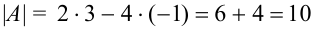
2. Найдем алгебраические дополнения каждого элемента матрицы :

Составляем матрицу из алгебраических дополнений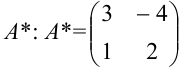

3. Транспонируем матрицу :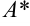

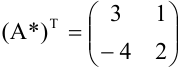
4. Составляем обратную матрицу по формуле:

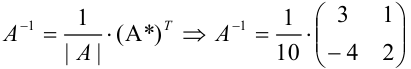
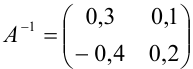
Проверим, действительно ли матрица 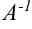является обратной к матрице . Должно выполняться равенство: 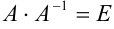, где 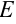— единичная матрица.

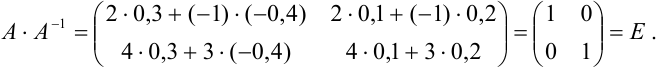
Получим, что 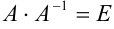, следовательно, матрица 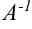является обратной к матрице .

Ответ: .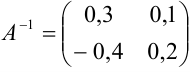

Пример №3.2.

Найдите матрицу, обратную матрице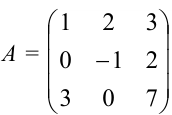

Решение:

1. Находим определитель матрицы .

Раскроем определитель по первому столбцу:

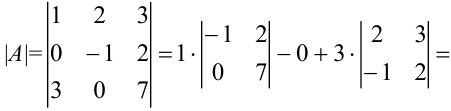
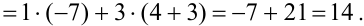
2. Найдем алгебраические дополнения каждого элемента матрицы :

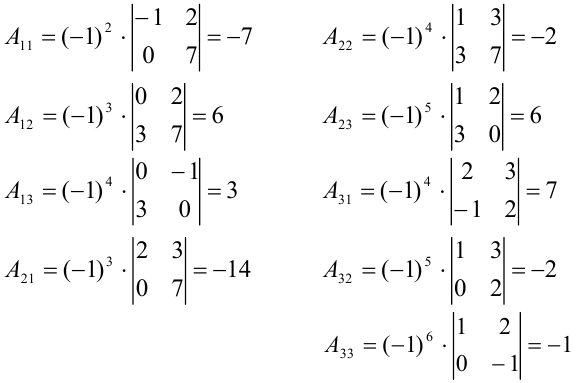
Составляем матрицу из алгебраических дополнений : .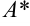

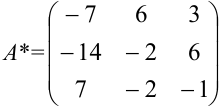3. Транспонируем матрицу : .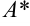

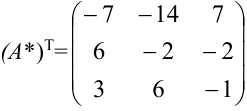4. Составляем обратную матрицу по формуле:

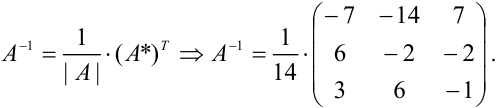
Ответ: .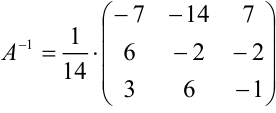

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Расчет определителей в электронных таблицах Microsoft Excel.

Понятие обратной матрицы.

Понятие ранга матрицы.

Понятие решения системы линейных уравнений.