Оглавление:
Алгебраические системы с тремя неизвестными
Для систем с тремя неизвестными определения понятий равносильности и следствия, а также свойства преобразований систем формулируются аналогично тому, как это было сделано для систем с двумя неизвестными.
Будем рассматривать системы вида
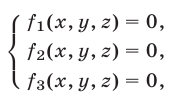
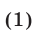
где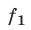 
, 
, 
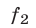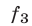являются либо многочленами от 
, 
, 
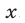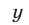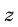, либо могут быть представлены в виде отношения многочленов.
Сформулируем для систем уравнений с тремя неизвестными следующие утверждения, которые могут оказаться полезными при решении систем.
1° Если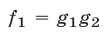 
, где 
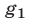и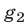 
—многочлены, то система (1) равносильна совокупности систем
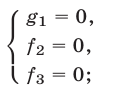
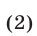
и
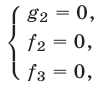
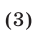
и поэтому множество решений системы (1) в этом случае есть объединение множеств решений систем (2) и (3).
2°. Если уравнение
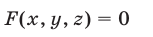
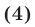
есть следствие системы (1), то система
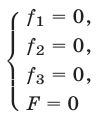
равносильна системе (1), т. е. при добавлении к системе (1) еще одного уравнения (4), являющегося следствием этой системы, получается система, равносильная системе (1).
3°. Если уравнение (4) — следствие системы (1), причем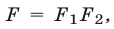 
где 
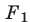и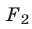 
—многочлены, то система (1) равносильна совокупности систем
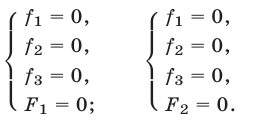
4°. Система (1) равносильна каждой из следующих систем:
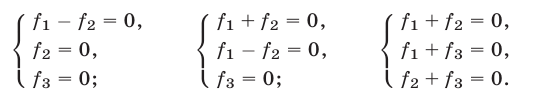
5°. Если уравнение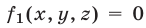 
равносильно уравнению 
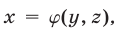где 
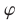— многочлен от 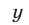и 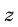, то система (1) равносильна системе
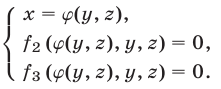
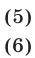
Это утверждение лежит в основе метода исключения неизвестных: система (1) сводится к системе (5), (6) с двумя неизвестными.
Прежде чем переходить к примерам алгебраических систем с тремя неизвестными, отметим, что нет общих рецептов для нахождения решений систем. Каждый раз нужно учитывать конкретные особенности рассматриваемой системы. Можно дать только общий совет: решайте побольше задач.
Рассмотрим сначала системы с тремя неизвестными, которые сводятся к кубическим уравнениям.
К таким системам относятся системы симметрических алгебраических уравнений, т.е. системы вида (1), где 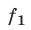, , 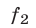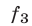— многочлены, каждый из которых не меняется, если поменять местами любую пару из переменных , , .
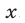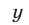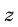В этом случае удобно ввести следующие переменные:
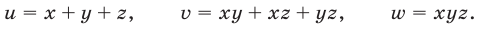
Простейший пример системы рассматриваемого вида — система
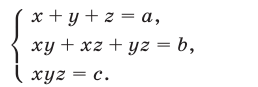
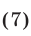
Система (7) и кубическое уравнение
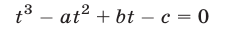
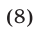
связаны следующим образом.
Если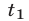 
, 
, 
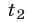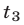— корни уравнения (8), то система (7) имеет шесть решений: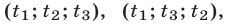 
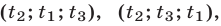
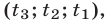
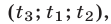получаемых всевозможными перестановками трех чисел 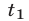, , 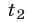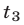. Обратно, если 
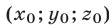решение системы (7), то 
, 
, 
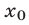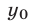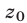— корни уравнения (8).
Доказательство этого утверждения основано на использовании формул Виета для корней уравнения (8):
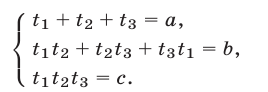
Для сведения к системам (7) систем симметрических уравнений вида
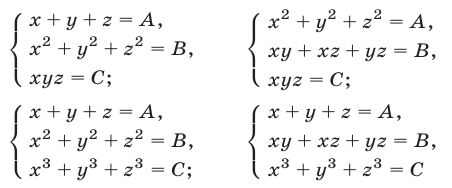
можно использовать следующие тождества:
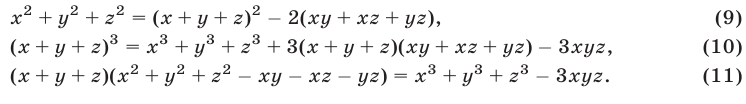
Примеры с решениями
Пример №186.
Решить систему уравнений
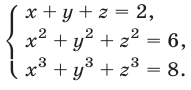
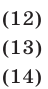
Решение:
Используя уравнения (12), (13) и тождество (9), получаем
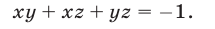
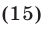
Применяя формулу (11) и учитывая равенства (13)-(15), находим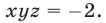 
Следовательно, исходная система равносильна системе вида (7), в которой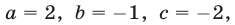 
, а уравнение (8) имеет вид
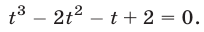
Корни этого уравнения — числа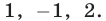 
Поэтому система имеет шесть решений, получаемых перестановкой чисел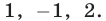
Ответ.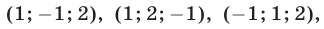 
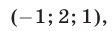
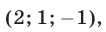
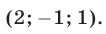
Обратимся теперь к системам с тремя неизвестными, которые не являются симметрическими.
Пример №187.
Решить систему уравнений
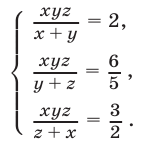
Решение:
Так как правые части уравнений отличны от нуля, то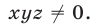 
Полагая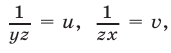 
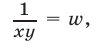получаем систему линейных уравнений
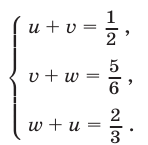
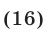
Сложив уравнения системы (16), находим
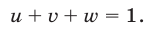
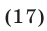
Из (16) и (17) получаем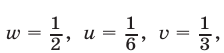 
т. е.
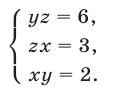
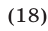
Перемножив почленно уравнения системы (18), которая равносильна исходной, имеем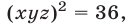 
откуда
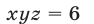
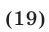
или
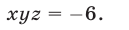
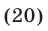
Следовательно, исходная система равносильна совокупности систем (18), (19) и (18), (20), которые имеют решения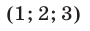 
и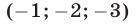 
соответственно.
Ответ.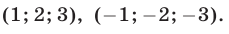 
Пример №188.
Решить систему уравнений
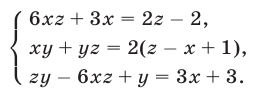
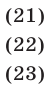
Решение:
Будем решать систему методом исключения неизвестных и сведением, в конечном счете, к одному уравнению с одним неизвестным. Складывая почленно уравнения (21) и (23), получаем
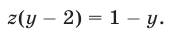
Так как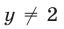 
на основании равенства (24), то из этого равенства следует, что
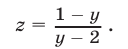
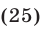
Запишем далее уравнение (22) в виде
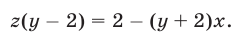
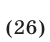
Исключив 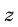из уравнений (24) и (26), получаем 
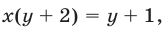откуда
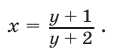
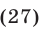
Заметим, что система (27), (25), (21) равносильна системе (21)— (23). Подставляя выражения для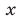 
и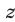 
из формул (27) и (25) в уравнение (21), получаем
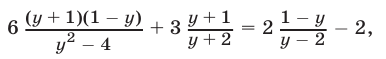
или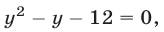 
откуда 
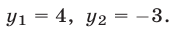Соответствующие значения 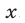и 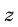найдем по формулам (27) и (25).
Ответ.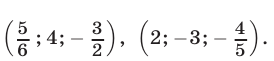 
Пример №189.
Решить систему уравнений
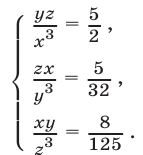
Решение:
Перемножив уравнения системы (28), получаем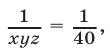 
или
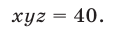
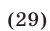
Уравнение (29) является следствием системы (28), которая равносильна системе
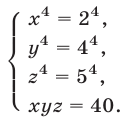
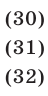
Уравнения (30), (31), (32) имеют решения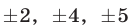 
соответственно. С учетом равенства (29) находим четыре решения системы (28).
Ответ.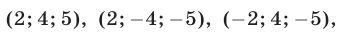 
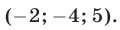
Пример №190.
Найти решения системы уравнений
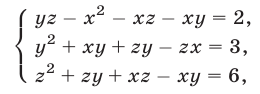
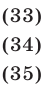
удовлетворяющие условию
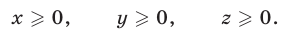
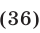
Решение:
Вычитая из уравнения (34) уравнение (33), получаем
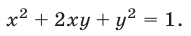
Далее, вычитая из уравнения (35) уравнение (33), находим
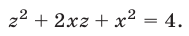
Наконец, складывая уравнения (34) и (35), получаем
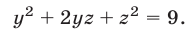
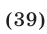
Система (37)-(39) равносильна системе (33)-(35), а при условии (36) — системе линейных уравнений
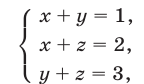
имеющей единственное решение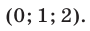
Ответ.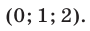
Пример №191.
Решить систему уравнений
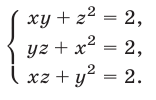
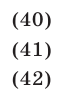
Решение:
Вычтем из уравнения (41) уравнение (40) и преобразуем полученное уравнение к виду
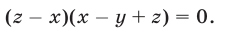
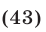
Выполнив ту же операцию с уравнениями (42) и (41), имеем
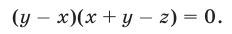
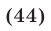
Система (43), (44), (42), равносильная системе (40)-(42), распадается на следующие четыре системы:
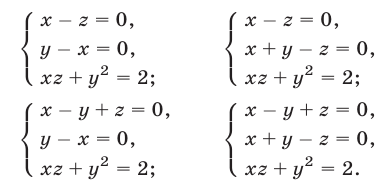
Полученные системы легко решаются методом исключения неизвестных. Объединив решения этих систем, найдем все решения исходной системы.
Ответ.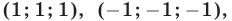 
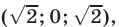
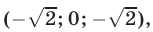
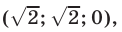
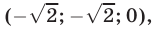
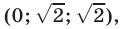
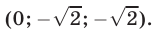
Пример №192.
Решить систему уравнений
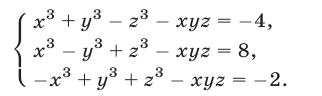
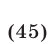
Решение:
Решим эту систему как линейную относительно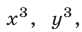 
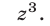Для этого сложим попарно уравнения системы (45) и получим систему
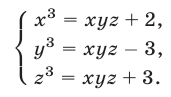
Перемножив уравнения системы (46) и полагая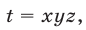 
находим 
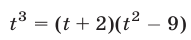или 
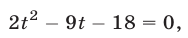откуда 
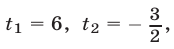т. е.
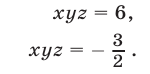
Система (45) в силу утверждения 3° равносильна совокупности систем (46), (47) и (46), (48), каждая из которых имеет единственное решение.
Ответ.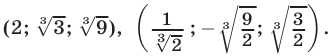
Пример №193.
Решить систему уравнений
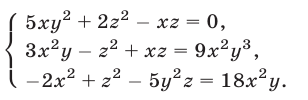
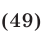
Решение:
Если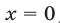 
, то из системы (49) следует, что 
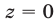, а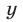 
может принимать любые значения. Аналогично, если 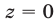, то 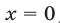, 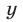— любое. Таким образом, система имеет бесконечное множество решений вида
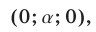
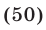
Будем искать решения системы (49) такие, что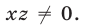 
. Умножив первое уравнение системы (49) на 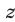, а третье — на 
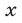и сложив результаты, получим
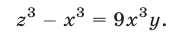
Прибавив к уравнению (51) второе уравнение системы (49), умноженное на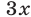 
:, находим
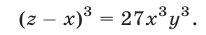
Каждое из уравнений (51), (52) является следствием системы (49).
Так как 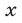, , 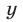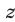— действительные числа (требуется найти действительные решения системы), то уравнение (52) равносильно уравнению
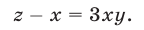
Исключая 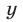из уравнений (53) и (51), получаем
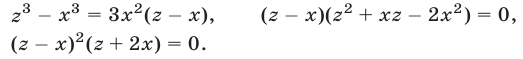
Уравнения (53) и (54) являются следствиями системы (49), а уравнение (54) равносильно совокупности уравнений
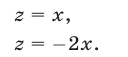
Из (55) и (53) следует, что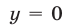 
, а из системы (49) пр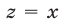и 
и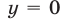 
находим 
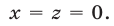Полученное решение содержится среди решений (50).
Из (56) и (53) следует, что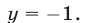 
Подставляя 
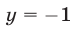в систему (49), находим решения 
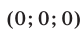и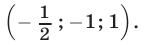
Ответ.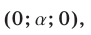 
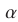— любое действительное число;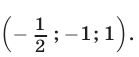 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
