Оглавление:


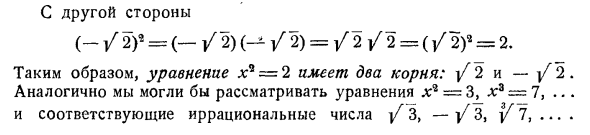
Алгебраические операции над действительными числами
- Вещественные алгебраические операции (продолжение). (3) Умножение. При рассмотрении умножения наиболее удобно начинать с положительного числа, а затем временно возвращаться к разделу положительных рациональных чисел, рассмотренному в параграфе. 4-7. Далее, класс (ab) as (c) и класс (AB) as (C) могут быть выполнены так же, как сложение. Аргументация остается той же, за исключением доказательства того, что, вероятно, все рациональные числа, кроме одного, принадлежат (с) или (С). Как и в дополнение, это зависит от того, могут ли a, b A и B быть выбраны так, чтобы C-c был сколь угодно малым.
Подать заявку здесь: C-c-AB-ab = (A-a) B — \ — a (B-b) Если вы принимаете положительный калибр, вы можете включить отрицательные числа в определение (_A) 3 = -a8, «(-p) = -ar, (-a) (-b) = ap. Наконец, установите (0) a = a (0) = 0 для всех a. (4) Отдел. Начните определять раскол Определите обратную (ненулевую) числовую величину а. Определите обратную величину положительного числа a, используя нижний и верхний классы, сначала ограничившись секциями положительных чисел и положительных рациональных чисел.Класс затем определить отрицательный ответ- Реальное уравнение — =
| Соотношения величины между действительными числами | Квадратичные иррациональности |
| Алгебраические действия над действительными числами | Некоторые теоремы о квадратичных иррациональностях |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Наконец, 3 Разделить на равенство Теперь его можно применить ко всем рациональным и иррациональным действительным числам и ко всем идеям и методам элементарной алгебры. Конечно, я не буду объяснять все детали здесь. Гораздо удобнее и интереснее обратить внимание на некоторые особые, но особенно важные классы иррациональных чисел. Пример VI. Докажите теорему, выраженную следующим уравнением. 1. aX1 = 1Xa = a. 2. «Х (1 / а) = 1. 4. «(футы) = (в кормовой части * 5. a (pt [-T) = a? 4.B. 6. (a-H) T = aT4-gT. 7. | aZ 1 = | | | (i |. 12. Число] / 2. Давайте вернемся к иррациональным числам, которые мы думали в этом абзаце. 4-5.
Таким образом, мы создали раздел, используя неравенства x1 2 и x1 ^> 2. Это был раздел полей только с положительными рациональными числами. Однако, если вы хотите заменить его на раздел в домене всех рациональных чисел (как описано в разделе 8), вы можете указать этот раздел или число как / 2. «Класс, который определяет произведение 2, сам является сущностью (aa ‘)}, где ana — положительное рациональное число меньше 2, а A и A — положительные рациональные числа (AA’).
Закончились все положительные рациональные числа. (/ 2) * = / 2/2 = 2.с другой стороны, Следовательно, уравнение x * = 2 имеет два пути. ■ / 2 и -j / 2. / 3, … Людмила Фирмаль

