Оглавление:
Алгебраические и трансцендентные числа
Помимо деления множества действительных чисел на непересекающиеся подмножества рациональных и иррациональных чисел, существует и другая их классификация. Так, действительные числа подразделяют на алгебраические и трансцендентные.
Алгебраическим, по определению, называют всякое действительное число, которое является корнем алгебраического уравнения n -й степени
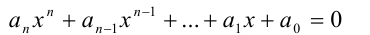
с рациональными коэффициентами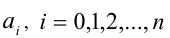 
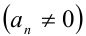. Таким образом, к алгебраическим относятся все рациональные числа, а из иррациональных — всевозможные алгебраические корни, например,
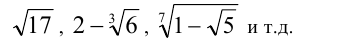
Все остальные действительные числа относятся к трансцендентным, например, это числа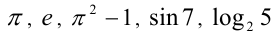 
и многие другие. Тот факт, что число е трансцендентно, был доказан в 1873 году Шарлем Эрмитом (1822— 1901), а трансцендентность числа 
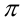доказал в 1882 году немецкий математик
Фердинанд Линдеман (1852-1939). Тем самым была доказана невозможность построения циркулем и линейкой квадрата, площадь которого была бы равна площади данного круга, т.е. в отрицательном плане была решена знаменитая проблема «квадратуры круга».
Пример №100.
Дано числовое выражение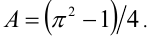 
Какое из следующих равенств может быть верным:
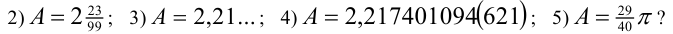
Решение:
1) Неверно, так как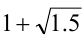 
— алгебраическое, 
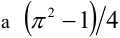— трансцендентное число; 2) неверно, так как 
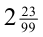— рациональное, 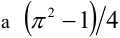иррациональное число; 3) может быть; 4) неверно, так как 
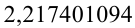— рациональное число; 5) неверно. Докажем методом «от противного». Предположим, что 
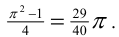Преобразуем это равенство к виду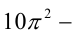 
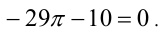Это означает, что число 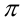является корнем алгебраического уравнения 
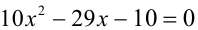, что по определению невозможно, так как 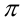-число трансцендентное. Ответ: может быть верным равенство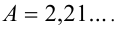 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
