Введем числа абсолютно нового для нас вида.
Числа вида 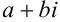 , где
, где 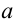 и
и 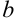 — действительные числа (
— действительные числа (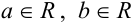 ), a
), a 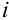 — мнимая единица, называются комплексными числами.
— мнимая единица, называются комплексными числами.
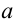 — действительная часть комплексного числа;
— действительная часть комплексного числа;
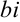 -мнимая часть комплексного числа (
-мнимая часть комплексного числа (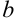 — коэффициент при мнимой части).
— коэффициент при мнимой части).
Запись комплексного числа в виде 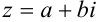 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Множество комплексных чисел принято обозначать буквой 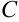 .
.
Встает вопрос: каким образом множество комплексных чисел соотносится с уже известными нам числовыми множествами 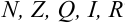 ?
?
Оказывается, любое действительное число является частным случаем комплексного, поскольку его можно представить в виде 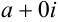 .
. 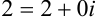 ,
, 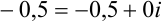 и т.д. Следовательно, множество действительных можно рассматривать как подмножество множества комплексных чисел. На диаграмме взаимосвязь всех известных нам числовых множеств будет выглядеть следующим образом (рис.42.1):
и т.д. Следовательно, множество действительных можно рассматривать как подмножество множества комплексных чисел. На диаграмме взаимосвязь всех известных нам числовых множеств будет выглядеть следующим образом (рис.42.1):
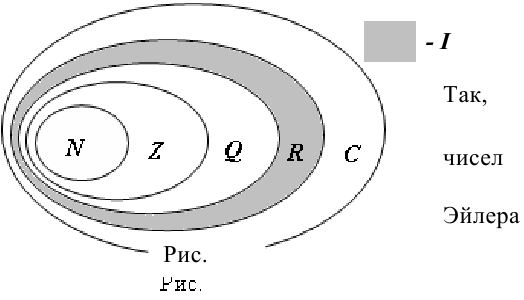
Справедлива цепочка вложения множеств: 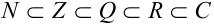 .
.
Комплексные числа вида 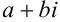 , у которых
, у которых 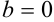 , называются действительными числами. Комплексные числа вида
, называются действительными числами. Комплексные числа вида 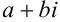 , у которых
, у которых 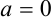 (вида
(вида 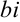 ), называются чисто мнимыми числами. Если
), называются чисто мнимыми числами. Если 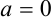 и
и 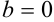 одновременно, то комплексное число
одновременно, то комплексное число 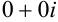 считают равным нулю.
считают равным нулю.
Два комплексных числа 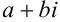 и
и 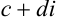 условились считать равными тогда и только тогда, когда равны их действительные части (
условились считать равными тогда и только тогда, когда равны их действительные части (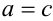 ) и коэффициенты при мнимой части (
) и коэффициенты при мнимой части (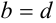 ).
).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
