Оглавление:
Агрегатная модель компонент уровня ряда динамики
Динамика рядов экономических показателей в общем случае складывается из четырех компонент:
- тенденции, характеризующей долговременную основную закономерность развития исследуемого явления;
- сезонной компоненты, связанной с влиянием сезонности развития изучаемого явления;
- циклической компоненты, характеризующей циклические колебания, свойственные любому воспроизводству;
- случайной нерегулярной компоненты как результата влияния множества случайных факторов.
Тенденцией называется общее направление развития, долговременная эволюция. В экономических рядах динамики можно выделить тенденцию трех видов: 1) среднего уровня; 2) дисперсии; 3) автокорреляции. Аналитическая тенденция выражается некоторой функцией времени, называемой трендом. Тренд характеризует основную закономерность развития явления во времени. График тренда — гладкая кривая, называемая траекторией. Считается, что основная тенденция является результатом влияния комплекса причин, постоянно действующих на изучаемый процесс в течение длительного периода, т.е. она характеризуется детерминированной составляющей ряда динамики.
Тенденция среднего уровня представима в виде графика временного ряда. Аналитически это функция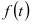 
, вокруг которой варьируют фактические значения изучаемого явления. В таком случае значения тренда в отдельные моменты времени являются математическими ожиданиями ряда динамики. Отклонения от тренда определяются случайной составляющей, характеризующей влияние случайных факторов.
Тенденция дисперсии характеризует тенденцию изменения отклонений эмпирических значений от значений, вычисленных по уравнению тренда. Тенденцию этого вида можно также изобразить графически.
Тенденция автокорреляции — это тенденция изменения связи между отдельными уровнями ряда динамики.
В рядах динамики можно наблюдать и различного рода периодические колебания с различной продолжительностью периода. Если периоды колебаний длительностью один год, они называются сезонными колебаниями. Сезонная компонента характеризует тип изменения, который регулярно повторяется во времени. Это изменение должно завершиться в пределах года и повторяться год за годом, чтобы квалифицироваться как сезонное изменение. Поэтому для выделения сезонной компоненты в динамическом ряду необходимо собрать данные за период больше года.
Сезонные колебания свойственны рядам, характеризующим рост объема реализации удобрений каждую весну и его сокращение в течение остальных месяцев, рядам, характеризующим потребление и производство сельскохозяйственной продукции и т.д.
Кроме тенденции и сезонной компоненты, в динамическом ряду выделяется циклическая компонента. Циклические колебания динамического ряда также являются повторяющимися и волнообразными, как и сезонные изменения. Но в отличие от сезонных изменений они обладают большой длительностью и меньшей возможностью прогнозирования по длительности и амплитуде. Так, например, не является редкостью циклическое изменение, требующее для своего завершения 4, 5 и более лет.
Таким образом, заметная долгосрочная компонента изменения динамического ряда, которая требует нескольких лет для своего завершения, называется циклической компонентой. Напомним, что долгосрочная компонента, лежащая в основе изменения динамического ряда, называется тенденцией. Важным примером циклической компоненты, которой экономисты уделяют значительное внимание, является деловой цикл.
В экономике изучаются также циклы с периодом колебаний равным 40 -60 лет (длинные волны); 15-20 лет (строительные циклы); 6-11 лет (главные циклы); 2-4 года (второстепенные (малые) циклы); от одного года до дести -двенадцати лет (экономические циклы); 24 месяца (подциклы МЭК).
Отметим, что автором концепции больших циклов конъюнктуры (или «длинных волн*’) периодичностью 40 — 60 лет является русский ученый Н.Д. Кондратьев. Концепция длинных волн приобрела широкую популярность в связи с изучением долговременных тенденций научно-технического прогресса.
Периодические колебания возникают, как правило, в результате суммирования большого числа случайных причин. Повторяющиеся же чередования подъема и спада в рядах динамики в большинстве случаев не характеризуются периодичностью.
Выделение циклической компоненты уровня динамического ряда производится при изучении циклов, если требуется измерить продолжительность отдельных этапов цикла. Компоненты, представляющие быстрые изменения (как правило, малой длительности) и не характеризующиеся наличием гладких размерных форм, образуют случайную (нерегулярную) компоненту. Случайная компонента порождается влиянием разнообразных событий на изучаемую величину. Так, случайную (нерегулярную) компоненту составляют ежедневные и еженедельные колебания уровня продажи некоторого товара, которые связаны с изменениями погоды и т.п.
Исследуемые динамические ряды могут представлять те или иные рассмотренные компоненты почти в чистом виде. Но в большей их части может проявляться как общая тенденция, так и некоторые сезонные изменения, на которые могут налагаться случайные флюктуации.
Для объяснения описываемого динамическим рядом процесса и использования результатов анализа при прогнозировании, уровни расчленяют на непосредственно не наблюдаемые компоненты и изучают в отдельности каждое из перечисленных выше движений. Указанные компоненты динамического ряда можно изобразить графически (см. рис.7.1)
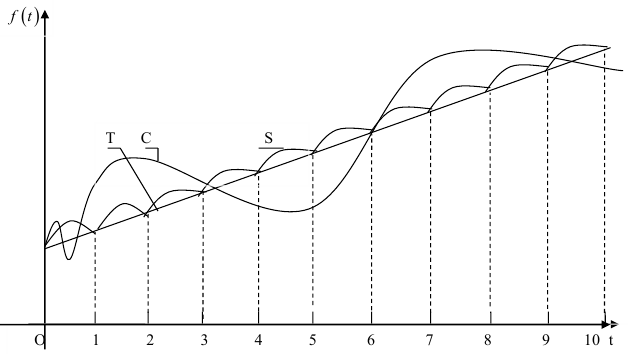
На рис. 7.1 данные динамического ряда за десть лет изображены волнистой линией с острыми гребешками. Линию тенденции представляет прямая, обозначенная буквой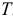 
. Сезонная компонента 
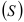характеризует увеличение в середине года, а затем спад. И так каждый год. Циклическая компонента обозначена буквой 
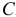, ее волны длиною 3-4 года. Случайная (нерегулярная) компонента обозначена буквой I.
При построении математической модели динамического ряда предполагают, что его уровни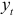 
являются суммой воздействующих величин:
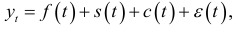
или произведением:
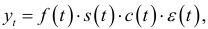
или это воздействие смешанное:
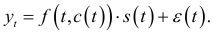
Здесь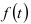 
— тенденция; 
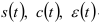, соответственно сезонная, циклическая и случайная (нерегулярная) компоненты; 
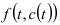— детерминированная составляющая, включающая тренд и циклические колебания.
Если перейти к логарифмам, то мультипликативную модель (7.16) динамического ряда можно привести к линейному виду
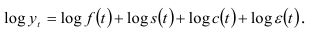
При выборе модели (7.2) слагаемое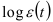 
рассматривается как случайная переменная 
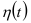с нулевым математическим ожиданием, и тогда формула (7.2) записывается в виде
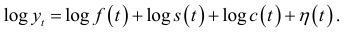
этом случае исходную модель (7.2) логичнее записать в виде
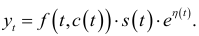
При допущении аддитивности компонент вклад сезонной компоненты остается на том же самом уровне для данной части года независимо от предельного уровня динамического ряда. При допущении мультипликативности компонент по мере возрастания предельных значений динамического ряда абсолютная величина сезонной колеблемости от периода к периоду также возрастает.
Пример 7.1.
Пусть временные ряды характеризуются следующими событиями: 1) школьные каникулы; 2) пониженный спрос на керосиновые примусы; 3) продажа елочных украшений; 4) повышенный спрос на гостиные гарнитуры в некотором городе; 5) продажа детских колясок. Укажем, какую из компонент характеризуют перечисленные временные ряды.
Временной ряд, характеризующий наступление и длительность школьных каникул, описывает циклическую компоненту, так как каникулы наступают в строго определенное время и имеют определенную продолжительность.
Уровни динамического ряда, характеризующего пониженный спрос на керосиновые примусы, определяют тенденцию. Сезонную компоненту временного ряда естественно связать с продажей елочных украшений, которые реализуются в канун Нового года. События 4 и 5 характеризуют случайную компоненту временного ряда.
Рассмотрим моделирование компонент ряда динамики.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
