Абсолютное, относительное и переносное движения точки
Довольно часто встречается движение точки, состоящее из нескольких движений. Вот два наглядных примера.
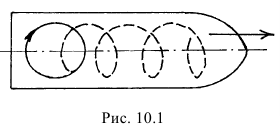
Первый. Наблюдатель, стоящий на высоком берегу реки, смотрит на
прямолинейно движущийся теплоход, на верхней палубе которого по окружности ходит пассажир (рис. 10.1). Наблюдатель же видит довольно сложную «загогулину» (пунктирная линия) как результат сложения прямолинейного движения и движения по окружности.
Второй пример. Стержень вращается в плоскости вокруг оси 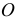 , а по нему движется колечко
, а по нему движется колечко 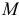 (рис. 10.2). Неподвижный наблюдатель увидит движение колечка по спирали.
(рис. 10.2). Неподвижный наблюдатель увидит движение колечка по спирали.
Эти движения имеют соответствующие названия: абсолютное, относительное и переносное.

Абсолютным движением называется движение точки, которое видит неподвижный наблюдатель («загогулина» и спираль в наших примерах).
Относительным движением — является движение точки, которое увидел бы наблюдатель, двигаясь вместе со средой (с теплоходом и со стержнем). В наших примеpax — это движение пассажира по
окружности на палубе теплохода и прямолинейное скольжение колечка по стержню.
Переносное движение — это движение среды, по которой движется точка (прямолинейное движение теплохода и вращение стержня).
При исследовании сложного движения точки полезно применять «Правило остановки». Для того чтобы неподвижный наблюдатель увидел относительное движение точки, надо остановить переносное движение. Тогда будет происходить только относительное движение. Относительное движение станет абсолютным. И наоборот, если остановить относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это переносное движение.
В последнем случае при определении переносного движения точки обнаруживается одно очень важное обстоятельство. Переносное движение точки зависит от того, в какой момент будет остановлено относительное движение, и от того, где точка находится на среде в этот момент, так как, вообще говоря, все точки среды движутся по-разному. Поэтому логичнее определять переносное движение точки как абсолютное движение той точки среды, с которой совпадает в данный момент движущаяся точка.
Так, переносное движение пассажира — это движение той точки палубы, на которой находится пассажир. И в примере с колечком — это движение той точки стержня, где находится колечко в данный момент (движение по окружности радиусом 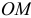 ).
).
Ещё несколько определений.
Абсолютной скоростью и абсолютным ускорением точки 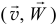 будем называть скорость и ускорение при абсолютном движении.
будем называть скорость и ускорение при абсолютном движении.
От носит ель но и скоростью и относительным ускорением 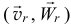 — скорость и ускорение точки в относительном движении.
— скорость и ускорение точки в относительном движении.
Переносная скорость и переносное ускорение точки
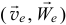 — это абсолютная скорость и абсолютное ускорение той точки среды, с которой совпадает движущаяся точка в данный момент времени.
— это абсолютная скорость и абсолютное ускорение той точки среды, с которой совпадает движущаяся точка в данный момент времени.
Все эти движения можно попробовать определить с помощью координат и векторным способом.
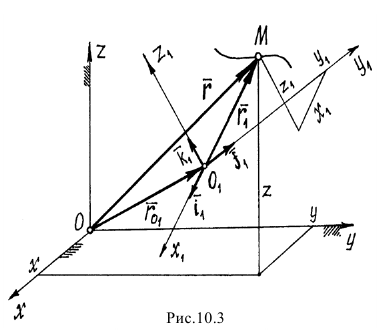
На рис. 10.3 показаны неподвижные оси 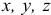 и движущиеся оси
и движущиеся оси 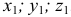 .
.
Конечно, абсолютное движение точки 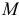 определяется уравнениями
определяется уравнениями
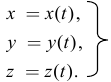
Относительное движение — в движущихся осях уравнениями
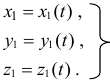
Уравнений, определяющих переносное движение точки, не может быть вообще. Так как, по определению, переносное движение точки  -это движение относительно неподвижных осей той точки системы
-это движение относительно неподвижных осей той точки системы  , с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
, с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
Абсолютное движение точки  определяется радиусом-вектором
определяется радиусом-вектором 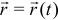 , а относительное движение радиусом-вектором
, а относительное движение радиусом-вектором 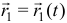 . Радиус-вектор
. Радиус-вектор 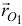 определяет движение начала подвижных осей
определяет движение начала подвижных осей 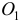 (но не переносное движение точки
(но не переносное движение точки 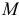 !).
!).
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| План скоростей |
| Ускорения точек тела. Мгновенный центр ускорений |
| Определение абсолютной скорости точки |
| Определение абсолютного ускорения точки |
