Абсолютное, относительное и переносное движения точки
Во введении в кинематику мы уже говорили, что всякое движение тела или точки есть движение относительное, т. е. его можно наблюдать и изучать лишь по отношению к другим телам и связанным с ними системам отсчета.
В предыдущих главах мы рассматривали движение по отношению к так называемой «неподвижной» системе отсчета, за которую в инженерной практике принимают обычно систему отсчета, жестко связанную с Землей.
Движение точки по отношению к системе отсчета, принимаемой за неподвижную, называется абсолютным движением.
В ряде случаев абсолютное движение точки бывает удобно рассматривать как сложное движение, состоящее из двух одновременных движений: движения точки по отношению к некоторой подвижной системе отсчета и движения точки вместе с подвижной системой отсчета по отношению к системе, принимаемой за неподвижную.
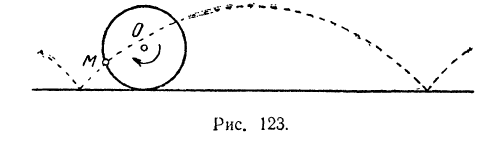
Так, например, движение какой-либо точки 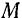 колеса тепловоза (рис. 123) относительно Земли происходит по кривой, называемой циклоидой. Его можно считать состоящим из двух движений: движения точки по окружности по отношению к корпусу тепловоза и движения этой точки вместе с поступательно движущимся корпусом тепловоза.
колеса тепловоза (рис. 123) относительно Земли происходит по кривой, называемой циклоидой. Его можно считать состоящим из двух движений: движения точки по окружности по отношению к корпусу тепловоза и движения этой точки вместе с поступательно движущимся корпусом тепловоза.
Движение точки по отношению к подвижной системе отсчета называется относительным движением.
Движение подвижной системы отсчета и всех неизменно связанных с ней точек по отношению к системе отсчета, принимаемой за неподвижную, называется переносным движением.
Чтобы определить переносные скорость и ускорение какой-либо точки  в произвольный момент времени, надо мысленно прекратить относительное движение данной точки и определить в этот момент ее скорость и ускорение по отношению к неподвижной системе отсчета как точки, неизменно связанной с подвижной системой.
в произвольный момент времени, надо мысленно прекратить относительное движение данной точки и определить в этот момент ее скорость и ускорение по отношению к неподвижной системе отсчета как точки, неизменно связанной с подвижной системой.
Аналогичным приемом бывает иногда удобно пользоваться и для выяснения относительного движения точки. Чтобы его определить, надо мысленно прекратить переносное движение точки.
В приведенном выше примере круговое движение точки 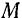 по отношению к движущемуся корпусу тепловоза есть, очевидно, относительное движение. Если эту точку мысленно неизменно связать с корпусом тепловоза, то ее движение вместе с ним будет переносным движением. Движение же точки
по отношению к движущемуся корпусу тепловоза есть, очевидно, относительное движение. Если эту точку мысленно неизменно связать с корпусом тепловоза, то ее движение вместе с ним будет переносным движением. Движение же точки 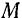 (по циклоиде) по отношению к Земле — абсолютное движение.
(по циклоиде) по отношению к Земле — абсолютное движение.
Приведем для пояснения еще несколько примеров. Движение человека по палубе движущегося по реке парохода есть движение относительное. Движение точки палубы парохода, в которой в данный момент находится человек, относительно берега реки — переносное движение, а движение человека относительно берега — абсолютного движение.
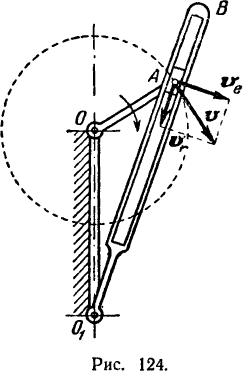
В механизме строгального станка (рис. 124) абсолютным движением точки 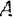 (центра шарнира, соединяющего ползун с кривошипом
(центра шарнира, соединяющего ползун с кривошипом 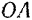 ) будет ее движение по отношению к неподвижной станине станка. Этим движением является, очевидно, круговое движение точки
) будет ее движение по отношению к неподвижной станине станка. Этим движением является, очевидно, круговое движение точки 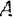 вокруг неподвижного центра
вокруг неподвижного центра 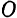 . Данное движение можно разложить на составляющие: движение точки
. Данное движение можно разложить на составляющие: движение точки 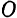 вдоль кулисы (подвижной направляющей)
вдоль кулисы (подвижной направляющей) 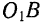 — относительное движение и вращательное (колебательное) движение вокруг центра
— относительное движение и вращательное (колебательное) движение вокруг центра 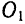 той точки кулисы
той точки кулисы 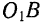 , с которой совпадает в данный момент точка
, с которой совпадает в данный момент точка 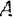 — переносное движение.
— переносное движение.
Еще раз подчеркнем, что термины «неподвижная» и «подвижная» системы отсчета имеют условное значение. Так, например, при рассмотрении движения точки колеса тележки, катящейся по палубе парохода, можно принять за «неподвижную» какую-либо систему отсчета, неизменно связанную с палубой (находящейся в движении по отношению к Земле).
Условимся в дальнейшем обозначать все кинематические характеристики, относящиеся к абсолютному движению точки, принятыми ранее символами, а характеристики, относящиеся к относительному и переносному движениям точки, теми же символами, но с подстрочными индексами: 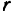 — для относительного движения (от латинского слова relativus—относительный) и
— для относительного движения (от латинского слова relativus—относительный) и 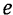 — для переносного движения (от французского слова entra-iner — увлекать с собой).
— для переносного движения (от французского слова entra-iner — увлекать с собой).
Абсолютной скоростью 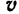 и абсолютным ускорением
и абсолютным ускорением 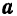 какой-либо точки
какой-либо точки 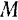 называется ее скорость и ускорение по отношению к системе отсчета, принятой за неподвижную.
называется ее скорость и ускорение по отношению к системе отсчета, принятой за неподвижную.
Относительной скоростью 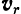 и относительным ускорением
и относительным ускорением 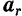 какой-либо точки
какой-либо точки 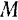 называется ее скорость и ускорение по отношению к подвижной системе отсчета.
называется ее скорость и ускорение по отношению к подвижной системе отсчета.
Несколько сложнее и требуют разъяснения понятия переносной скорости и переносного ускорения точки в тех случаях, когда движение подвижной системы отсчета не является поступательным.
Так, в приведенном выше примере переносным движением точки 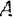 (центра шарнира ползуна) является абсолютное движение, т. е. движение по отношению к неподвижной системе отсчета (к станине станка) той точки кулисы, с которой совпадает в данный момент точка
(центра шарнира ползуна) является абсолютное движение, т. е. движение по отношению к неподвижной системе отсчета (к станине станка) той точки кулисы, с которой совпадает в данный момент точка 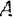 . Но при вращении кулисы около неподвижной точки
. Но при вращении кулисы около неподвижной точки 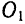 различные точки кулисы, находящиеся на различных расстояниях от точки
различные точки кулисы, находящиеся на различных расстояниях от точки 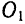 и имеют различные скорости и ускорения, и потому переносные скорость и ускорение точки
и имеют различные скорости и ускорения, и потому переносные скорость и ускорение точки 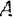 будут зависеть от того, какое положение эта точка занимает в данный момент по отношению к кулисе.
будут зависеть от того, какое положение эта точка занимает в данный момент по отношению к кулисе.
Таким образом, переносной скоростью 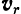 и переносным ускорением
и переносным ускорением 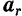 какой-либо точки
какой-либо точки 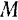 называется абсолютная скорость и абсолютное ускорение той, неизменно связанной с подвижной системой отсчета точки, с которой совпадает в этот момент данная точка
называется абсолютная скорость и абсолютное ускорение той, неизменно связанной с подвижной системой отсчета точки, с которой совпадает в этот момент данная точка 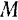 .
.
Так как только при поступательном движении подвижной системы отсчета скорости и ускорения всех связанных с ней точек одинаковы, то только в этом случае переносная скорость и переносное ускорение движущейся точки не будут зависеть от ее положения относительно подвижной системы отсчета и под ними в этом случае можно понимать скорость и ускорение любой точки подвижной системы отсчета относительно неподвижной.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
